Задача №1. Расчёт линейной электрической цепи постоянного тока

Введение

Из всех видов энергии в настоящее время наиболее широко применяется электромагнитная энергия, которая на практике обычно называют электрической.

Энергия – это количественная мера движения и взаимодействий всех форм материи. Для любого вида энергии можно назвать материальный объект, который является её носителем. Использованием этих явлений для получения, передачи и преобразования энергии занимается электротехника. Широкое применение электромагнитного поля и его энергии объясняется их ценными свойствами, взаимностью эффективного преобразования в другие виды энергии (механическую, тепловую, световую, химическую) с цепью приведения в движение машин и механизмов, получение тепла и светла, изменение химического состава вещества, производства и обработки материалов и т.д.

Интенсивное использование электрической энергии связанно со следующими её особенностями: электрическую энергию сравнительно получить из других видов энергии (механической, тепловой, атомной), передать с малыми потерями на большие расстояния и преобразовать в другие виды энергии. Благодаря этим свойствам, энергия, сосредоточенная в природе (энергия падающей волны, торфа, угля и т.д.), сравнительно легко распределяется по самым различным приёмникам. Электрическая энергия относится к чистым видам энергии. Одной из самых актуальных задач является проблема охраны окружающей среды от загрязнения, связанного с производством электрической энергии и переработки её в другие виды энергии. Для этого реконструируется и модернизируется действующее оборудование, вводятся автоматизированные системы контроля загрязнения воздушного бассейна выбросами ТЭС, АЭС, на электрических станциях используются очистительные сооружения, замкнутые циклы использования воды и т.д.

В данной курсовой работе мы решали определённые задания по предмету “Теоретические основы электротехники”, которые базируются на расчёте линейных и нелинейных электрических цепей постоянного тока, а также линейных цепейпеременного тока: однофазный, трёхфазный, исследование переходных процессов в электрических цепях.

Задача №1. Расчёт линейной электрической цепи постоянного тока.

Для электрической цепи (рис. 1.14) выполнить следующее:

1) начертить схему цепи и показать направление токов во всех ветвях цепи;

2) определить эквивалентное сопротивление цепи R_э;

3) рассчитать токи в каждом резисторе;

4) рассчитать ток в электрической схеме в режиме короткого замыкания;

5) составить баланс мощностей для заданной схемы.

6) построить потенциальную диаграмму для любого замкнутого контура цепи, включающего ЭДС.

Числовые параметры схем электрических цепей постоянного тока.
Таблица 1

№ варианта	№ схемы	Iкз,А	r,Ом	R1 ,Ом	R2 ,Ом	R3 ,Ом	R4 ,Ом	R5 ,Ом	R6 ,Ом	R7 ,Ом
	1.14	35,82	0,67			3,5		4,5

Решение:

1. Вычертим схему соединений элементов цепи и укажем направление токов на отдельных участках цепи.

Рис. 1.14

2. Определи ЭДС источника тока в данной схеме, зная ток короткого замыкания и внутреннее сопротивление источника, используя закон Ома:

Iкз =

E=Iкз*r=38,82 (А)*0,67 (Ом)=26,01 (В)

3.Найдем эквивалентное сопротивление цепи, но перед этим свернем схему и найдем все сопротивления по закону Ома:

R1,2=R1*R2/(R1+R2)=2*6/(2+6)=1,5 (Ом)

RA=R1,2*R3/(R1,2+R3+R4)=1,5*3,5/(1,5+3,5+10)=0,35 (Ом)

RB=R3*R4/(R1,2+R3+R4)=3,5*10/(1,5+3,5+10)=2,33 (Ом)

RC=R1,2*R4/(R1,2+R3+R4)=1,5*10/(1,5+3,5+10)=1 (Ом)

RB,5=RB+R5=2,33+4,5=6,83 (Ом)

RC,6,7=RC+R6,7=1+4,2=5,2 (Ом)

R6,7=R6*R7/(R6+R7)=14*6/(14+6)=4,2 (Ом)

RB,C,5,6,7=RB,5*R6,7,C/(RB,5+R6,7,C)=6,83*5,2/(6,83+5,2)=2,95 (Ом)

RЭ= RA+RB,C,5,6,7=0,35+2,95=3,3 (Ом)

4. Найдем силу тока в неразветвленной части цепи по закону Ома:

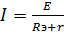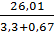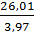= = = 6,55 (А).

5. Найдем напряжение на зажимах источника U:

U=I*Rэ=6,55*3,3=21,62 (В);

6. Рассчитаем силу тока на отдельных участках цепи по закону Ома:

IA=IB,C,5,6,7=I=6,55 (А);

UB,C ,5,6,7=IB,C,5,6,7*RB,C,5,6,7=UB,5=U6,7,C=6,55*2,95=19,32 (B);

IB,5=UB,5/RB,5=19,32/6,83=2,83 (А);

I6,7,C=U6,7,C/R6,7,C= 19,32/5,2=3,72 (А);

IB=I5=IB,5=2,83 (А);

IC=I6,7=IC,6,7=3,72 (А);

I5*R5 - I6,7*R6,7= 2,83*4,5 – 3,72*4,2= 12,74 -15,62 = 2,88

I4=2,88/10=0,29 (А);

I1,2= I4+IB= 0,29+2,83= 3,12 (А);

I3=I6,7+I4=3,72+0,29=4,04 (А);

U6=U7=U6,7=I6,7*R6,7=3,72*4,2=15,62 (B);

I6=U6/R6=15,62/14=1,12 (А);

I7=U7/R7=15,62/6=2,61 (А);

U1,2=U1=U2=I1,2*R1,2=3,12*1,5=4,68 (B);

I1=U1/R1=4,68/2=2,34 (А);

I2=U2/R2=4,68/6=0,78 (А).

Результаты расчета тока представлены в таблице 2:

I,A	I1,A	I2,A	I3,A	I4,A	I5,A	I6,A	I7,A
6,55	2,34	0,78	4,01	0,29	2,83	1,12	2,61

7.Составляем баланс мощностей для заданной схемы:

E*I=I1²*R1+I2²*R2+I3²*R3+I4²*R4+I5²*R5+I6²*R6+I7²*R7+I*r;

Подставляем численные значения и вычисляем:

26,01*6,55=2,34²*2+0,78²*6+4,01²*3,5+0,29²*10+2,83²*4,5+1,12²*14+2,61²*6+ +6,55²*0,67;

170,36=10,95+3,65+56,28+0,84+36,04+17,56+40,87+4,38;

170,36(Вт)=170,57(Вт).

С учётом погрешности расчётов баланс мощностей получился.

8. Построим потенциальную диаграмму для замкнутого контура цепи, включающего ЭДС. Для этого на схеме выделим замкнутый контур АБВГД, заземлив точку А.

Рассчитаем потенциальные точки Б, В, Г, Д. Зададимся обходом контура по часовой точке. Потенциал заземленной точки А- =0.

Зная величину и направление токов ветвей и ЭДС, а также величины сопротивлений R1, R4, R7 и r вычислим потенциалы всех точек контура при переходе от элемента к элементу. Начнем обход от точки А :

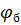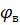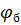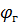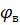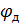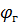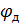= -I*R1 ; = -I*R4; = -I*R7; = -I*r; = +Е.

Найдем ток: I =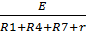
I = 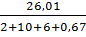= = 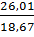1,39 (A);

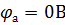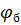; =0-(1,39*2)=-2,78(В); 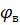=(-2,78)-(1,39*10)=-16,68(В); 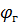=(-16,68)-(1,39*6)=-25,02(В); 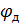=(-25,02)-(1,39*0,67)=-25,95(В); =(-25,95)+26,01= 0,06(В)

Построим потенциальную диаграмму. По оси абсцисс откладываем сопротивление контура в той последовательности, в которой производим обход контура, прикладывая, сопротивления друг друга, по оси ординат – потенциалы точек с учетом их знаков.

R, Ом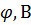
	-2,78
	-16,68
	-25,02
18,67	-25,95
26,01	0,06