Обобщенный метод наименьших квадратов для смягчения гетероскедастичности и устранения автокорреляции

а) смягчение гетероскедастичности

Если известна причина (и, соответственно, форма гетероскедастичности), то для ее устранения можно воспользоваться обобщенным методом наименьших квадратов (ОМНК).

Предположим, что дисперсия регрессионных остатков связана с некоторой переменной z_t зависимостью вида

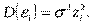
В качестве переменной может быть:

1) среднее квадратическое отклонение σ_t(если она известна), в этом случае получают взвешенный метод наименьших квадратов (ВМНК);

2) x_iили , т.е. дисперсия отатков пропорциональна либоx_iлибо .

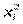Для того чтобы избавиться от гетероскедастичности, необходимо разделить каждый член регрессионного уравнения

(*)

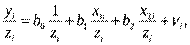где 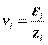случайная ошибка.

Поскольку 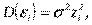то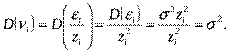

Таким образом, ошибки в уравнении (*) будут гомоскедастичными.

Однако на практике часто не удается с уверенностью определить причину и форму гетероскедастичности. В этом случае можно либо перевести все переменные в логарифмическую форму (однако необходимо помнить, что этот прием неприменим, если переменные модели могут принимать нулевые или отрицательные значения), либо воспользоваться специальными робастными методами оценки.

б) устранение автокорреляции

Для устранения автокорреляции (как и в случае с гетероскедастичностью) можно воспользоваться обобщенным методом наименьших квадратов (ОМНК).

Для применения ОМНК необходимо специфицировать модель автокорреляции регрессионных остатков. Обычно в качестветакой модели используется авторегрессионный процесс первого порядкаAR(1).

1. Используя AR(1) в качестве модели автокорреляции остатков, можно записать:

(1)

2. Предполагая, что структура модели является постоянной, для периода t -1 получаем модель:

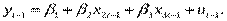(2)

Умножаем обе части уравнения (2) на ;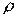

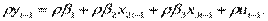(3)

2. Вычитаем уравнение (3) из уравнения (1):

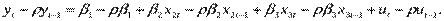(4)

2. Приводим уравнение (4)к виду:

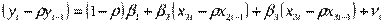(5)

где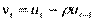

6) Вводим переменные

,

,

,

.

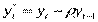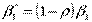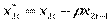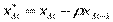и переписываем уравнение (5) в виде:

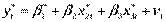. (6)

Ошибки полученного уравнения (6) не подвержены автокорреляции, поэтому на данном этапе можно применить к модели метод наименьших квадратов.

Стоит заметить, что прежде чем переходить к оценке уравнения (6), надо сначала оценить величину 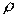— заранее онанеизвестна (приближенно оценить ее можно, например, через статистику Дарбина - Уотсона: 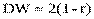, т.е. .

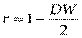21.Метод наименьших квадратов: назначение, условия применения.
Условия применения МНК:

§ модель регрессии должна быть линейной по параметрам

§ х – не стохастическая переменная (заданная величина)

§ значения ошибки – случайные. Их изменение не образует определенной модели

§ число наблюдений должно быть больше числа оцениваемых параметров (5-6 раз)

§ значения переменной x не должны быть одинаковыми

§ изучаемая совокупность должна быть достаточно однородной

§ отсутствие взаимосвязи между фактором x и остатком

§ модель регрессии должна быть корректно специфицирована

§ в модели не должно наблюдаться тесной взаимосвязи между факторами