Кешігуші, тармақталған жіне айнымалы параметрлі сызықтық жүйелер

Кешігетін сызықты жүйлер деп бір немесе бірнеше кешігуші үзбелерден құралған сызықты автоматты реттеу жүйелерін атаймыз.

Кешігуші болып әдетте реттелуші объектілер болады және элементтері әрқашанда кешігуді болдырмайтындай етіп таңдап алынатын басқару жүйелері де өте сирек бола алады.

Кешігуші болып объектілерге мысал болып шар тәрізді немесе өзекті диірмен, кептіргіш немесе күйдіргіш пеш, тұндырғыш немесе флатационды машиналар бола алады. Осы объектілердің барлығындағы кірісіндегі әсердің өзгерісі уақыт бойынша шығысқа, он минутқа дейін кешігіп беріледі.

Кешігу жүйесінің теңдеуі қарапайым жүйелерде сияқты құрылады.

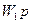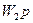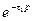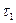9.1.суретте кешігуші жүйенің құрылымдық схемасы келтірілген, ол беріліс функциясы және екі сызықты үзбеден және беріліс функциялары мен ( мен 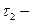кешігу тұрақтылары) екі кешігу үзбелерінен құралған.

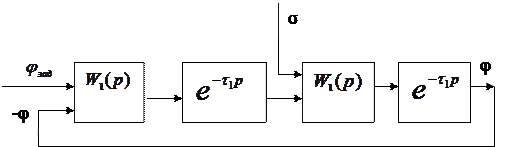
9.1.Сурет. Кешігуі бар жүйенің структуралық схемасы

Ажыратылған жүйенің беріліс функциясы жүйеге кіретін үзбелердің беріліс функцияларының туындысын береді.

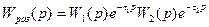(9.1)

Кешікпейтін үзбелердің беріліс функциясы мен кешігуші үзбелердің беріліс функцияларын біріктіріп, мынаны аламыз

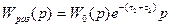(9.2)

Мұндағы 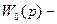кешігуді есептемегенде сызықты жүйенің беріліс функциясы. Мұндай жүйені кейде шекті деп атайды.

Көпконтурлы жүйелер жағдайында нәтижелі беріліс функциялары күрделірек болады, бірақ олар кешігусіз жүйелерге жататын ережелер бойынша құрылады.

Кешігетін автоматты реттеу жүйесін қарастырайық , 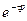көбейткішінің бар болуы сипаттамалық теңдеудің шексіз түбірлер саны болуына алып келеді.

Үшінші ретті және одан жоғары жүйелердің тұрақтылығын анықтау үшін Гурвиц критериясы пайдаланылмайды, Михайлов критериясын пайдалану күрделі болып табылады. Ең оңайы Найквист критериясы көмегімен тұрақтылықты анықтау болып табылады, ол төменде келтіріледі.

Бір кешігу үзбесі бар автоматты реттеу жүйесін қарастырайық. Оны екі бөлікке бөлеміз – кешігусіз сызықты бһлік немесе беріліс функциясы 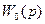шекті жүйе мен беріліс функциясы 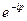кешігуші үзбеге, олар бір – бірімен тізбектеп қосылған (9.2сурет). Барлық жүйенің нәтижелі беріліс функциясы тізбектеп қосылған элементтердің беріліс функциясының туындысы ретінде аламыз.

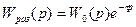(9.3)

Кешігуші жүйенің амплитуда – фазалық сипаттамасының теңдеуін (9.3) өрнегіндегі p- ны 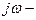ға алмастырып аламыз

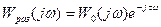(9.4)

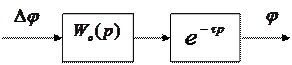
9.2.Сурет. Кешігуі бар ажыратылған жүйенің структуралық схемасы

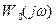комплекстік өрнекті көрсеткіш түрінде көрсетеміз.

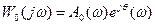(9.5)

мұндағы 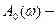шекті жүйенің жиіліктік функциясның модулі.

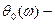осы функцияның аргументі

(9.5) өрнегіндегі 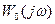мәнін (9.4) теңдеуге қойып шығып мынаны аламыз.

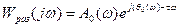(9.6)

(9.6) теңдеуінен кешігуші жүйенің амплитуда – фазалық сипаттамасын құру үшін шекті жүйенің амплитуда – фазалық сипаттамасын құру қажет және осы жүйенің әрбір радиус – векторын сағат тілімен 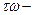ға тең бұрышқа бұру қажет екені шығады.

Шекті жүйе тұрақты жіне оның амплитуда – фазалық тең бұрышқа бұру қажет екені шығады.

Шекті жүйе тұрақты және оның амплитуда – фазалық сипаттамасы координатасы 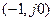нүктесін қамтымайды деп болжайық. (9.3 сурет, 1 қисық). Координата бас нүктесінен бірлік деп аталатын шеңбер жүргіземіз, ол шеңбер 1- қисықпен қилысатын А нүктесінен өтеді және А нүктесіне сәйкес жиілікті 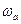деп, ал ОА радиус – векторы мен теріс таңбалы нақты жартылай өсь арасындағы бұрышты 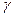арқылы белгілейміз.

Барлық радиус – векторларынын 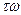бұрышқа бұрылып кешігетін жүйенің амплитуда – фазалық сипаттамасын құраймыз, 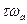бұрышының мәні әзірге мына теңсіздікті қанағаттандырады.

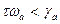(9.7)

амплитуда – фазалық сипаттамасы 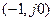нүктесін қамтымайды және жүйе тұрақты болып қалады. Егер 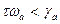болса, амплитуда – фазалық сипаттама нақты өсьті 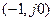нүктесінде қиып өтеді де, жүйе тұрақтылық шекарасында орналасады. Егер 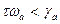болса, кешігу жүйесі тұрақсыз. Мына қатынас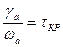

критикалық уақыт кешігуі деп аталады.

Осылай, тұрақты кешігетін жүйе ажыратылған күйде тұрақты,ол тұрақталған күйде тұрақты болады, егер оның амплитуда – фазалық сипаттамасы 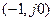координатты нүктесін қамтымаса.

Егер шекті жүйе тұрақталған күйде тұрақсыз болса, онда кешігу жүйесі де көп жағдайларда тұрақсыз. Дегенмен шекті жүйенің амплитуда – фазалық сипаттамасы бірлік шеңбер оны бірнеше нүктеде кесіп өтетін түрде болатын жағдайлар да мүмкін. Содан тұрақсыз шекті жүйе нақты кешігу мәндері кезінде тұрақты болуы мүмкін.

Кешігетін жүйе сапасын өтпелі процестің қисығын нақты жиіліктік сипаттамалар көмегімен құру арақылы зерттеуге болады. Дегенмен қазіргі уақытта мұны модельдеуші есептеу машиналарының көмегімен қолайлы және жылдам орындауға болады .

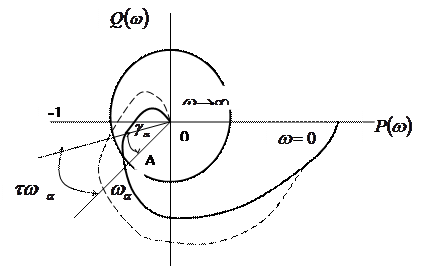
Рис. 9-3. Кешігуі бар жүйенің амплитуда-фазалық сипаттамасы

Тармақталмаған параметрлі сызықты жүйелер деп геометриялық өлшемдері үлкен болуы салдарынан параметрлерін бір нүктеге шоғырланған деп санауға болмайтын ұзын құбырлардан немесе ұзындығы үлкен электрлік желілерінен құралған осындай сызықты автоматты реттеу жүйелерін айтамыз.

Жоғарыда көрсетілгендей, тармақталған параметрлі жүйелер тау – кен өнеркәбінде қолданылмайды.

Тармақталған параметрлі жүйелерді зерттеу кезінде дербес туынды дифференциялдық теңдеу аппараты қолданылады, олардың көмегімен құбырлар мен электр желілердегі толқынды процестер ескеріледі. Түрлендіргеннен кейін кешігуші жүйе теңдеулеріне ұқсас дифференциалды теңдеулер алынады. Тармақталған параметрлі жүйенің сапасы мен тұрақтылығын зерттеу кешігуші жүйелердегі сияқты теңдеулер бойынша жүргізіледі.

Айнымалы параметрлі сызықты жүйелер дегеніміз реттелетінобъектінің параметрлері уақыт бойынша өзгеретін осындай сызықты автоматты реттеу жүйелер.

Параметрлері айнымалы объектілерге мысал болып шар тәрізі диірмен бола алады, оның статикалық және динамикалық сипаттамалары сипаттамасы кескіш тістерінің мұқалту шамасында уақыт бойынша өзгеретін көмір байыту комбайндардың майдалау шарларының шығындауымен уақыт бойынша өзгереді. Айнымалы параметрлерінде кейбір қозғалмалы объектілер бар – массасы мен инерция моменті жанармайдың жанып кету шамасы бойынша өзгеретін ұшақ, ракета (зымыран).

Реттелетін объектінің параметрлерін өгерту уақыт бойынша айнымалылар дифференциалдық теңдеу коэффициенттері болуын табылуына алып келеді.

Қазіргі уақытта бірінші ретті теңдеулермен және кейбір жағдайларда екінші ретті теңдеулермен жазылатын айнымалы парамтрлі жүйелерді зерттеудің жалпы әдістері өңделіп шығарылды.

Зерттеу жеткілікті күрделі және де сол уақытта жеткіліксіз толық болып табылады.

Айнымалы параметрлі жүйелерді математикалық әдістермен синтездеу мүмкін емес және өтпелі процестердің қажетті сапасын қамтамасыз ететін қолайлы түзеткіш құрылғыларды таңдап алу жұмысының аса маңызды режимдерін қарастыру жолымен мүмкіндік беретін электронды есептеу машиналарының көмегімен жүзеге асыруға болады.

Өтпелі процесс уақытында жүйе параметрлері мәнсіз өзгеретін жағдайларда (квазистационарлы жүйелер) жүйені талдау және түзеткіш құрылғыларды мұздатқыш коэффициенттер әдісімен синтездеуге болады. Бұл әдістің мәні параметрлерге, және сәйкесінше коэффициенттерге параметрлердің қарастырылған уақыт аралығында өзгеру диапазонының шегінде әртүрлі уақыт моменттеріне сәйкес тұрақты мәндер беріледі. Айнымалы параметрлі жүйелер тұрақты параметрлі жүйелерге сәйкес келеді, оларды алдыңғы бөлімдерде ідңстермен синтездейді және талдайды.

Мұндай зерттеу өзінің еңбекті көп қажет ететіндегімен ерекшеленеді, өйткені оны параметрлердің қатайтылған мәндері үшін тізбектей жүргізу қажет. Бұл кезде барлық маңызды варианттар мен олардың мәндерін қамту үшін параметрлерді қатайтылған уақыт моменттерін дұрыс таңдап алу маңызды.

Егер параметрлердің өзгеру диапазонындағы барлық мәндерінде реттеу жүйесінің сапасы берілген талаптарға сәйкес келсе, онда сапа қанағаттанарлық болып табылады.

Негізгі әдебиет: 3 [7-49; 244-324].

Қосымша әдебиет: 1 [336-364]

Бақылау сұрақтары:

1. Қандай сызықты жүйелер ерекшеге жатады?
2. Кешігуші сызықты жүйелердің ерекшеліктері қандай?
3. Кешігуші сызықты жүйелердің беріліс функциясы қалай алынады?
4. Сызықты кешігу жүйесін Найквистің тұрақтылық критериясның көмегімен тұрақтылыққа қалай зерттеу керек?
5. Тармақталған параметрлі жүйе сапасын қалай зерттеуге болады?
6. Тармақталған параметрлі сызықты жүйелердің қандай ерекшеліктері бар?
7. Айнымалы параметрлі сызықты жүйелердің ерекшелігі қандай?
8. Айнымалы параметрлі сызықты жүйелер қандай түрде зерттеледі?

№ 12. Дәрістің конспектісі

Дәрістің тақырыбы: Ерекше сызықты автоматты реттеу жүйелері (Сызықты жүйелердің алуан түрлері. Кешігуші, тармақталған және айнымалы параметрлі сызықты жүйелер. түрлендірудің негізгі түсініктемелерін импульсті реттеу принципі).

Импульстік реттеудің сызықты жүйесі деп жазылған үздіксіз әрекеттегі үзбелерден бөлек импульсті үзбеден құралған сызықты автоматты реттеу жүйесін атаймыз.

Импульстік үзбе дегеніміз үздіксіз кіріс әсері тұрақты немесе айнымалы амплитудалы импульстерге түрленетін және басы бір бірінен кейін бірдей уақыт аралығы арқылы жүретін ұзындықтағы үзбені айтамыз.

Импульсті жүйелер сәйкес үздіксіз жүйелерге қарағанда біршама аз дәлдікті береді, өйткені реттеу тізбегінің периодты түрде ажырауының салдарынан процестің жүрісі жөніндегі ақпараттардың кейбір бөліктері жоғалады. Егер басынан бірінің артынан бірі жүретін импульстер арасындағы уақытты маңызды басқару өзгерісінің уақытымен салыстырғанда үлкен қылып қабылдасақ, онда импульстік жүйе тіпті жұмысқа қабілетсіз болып шығады.

Дегенмен нақты шарттарда кқршілес импульстердің басы арасындағы уақыт әрқашанда ақпараттар байқала жоғалуы болмайтындай және реттеудің қажетті дәлдігі қамтамасыз етілетіндей етіп таңдап алынуы мүмкін. Бұл жағдайда импульстік жүйелерде үздіксіздермен салыстырғанда кейбір маңызды ерекшеліктері бар. Сонымен сезімтал элементтердің шектелген қуаты кезінде импульстік жүйелер көп күш жұмсамай қуатты жүйелерді басқара алады. Басқару әсерлерін арақашықтыққа беру кезінде олады бөгеттерді тозған әсерін азайтуүшңн және бір арна бойынша бірнеше шамаларды беру үшін импульстік түрге түрлендірген қолайлы. Дискреттік ақпаратты беретін сандық есептеу машиналары үшін пайдаланған жағдайда тек импульстік жүйелерді пайдалануға болады.

Импульстік жүйелер баяу өзгеретін процестерді реттеу үшін(температураны, қысымды және т.б. реттеу) жиә қолданылады.

Реттелетін шаманың нақты дұрыс мәні берілгеннен ауытқуына пропроционал әсерлі импульсті реттеудің тұрақталған жүйелерінде импульстер болатын уақыт аралығы беріледі, яғни жүйе тұрақталған кезде. Импульстар арасындағы аралықтағы жүйе ажыратылған сияқты жұмыс істейді. Импульсті реттеу жүйелерінде үш типті үзбелер пайдаланылады.

Бірінші типке импульстік үзбелер кіреді, оның үздіксіз кіріс шамасы импульстер тізбегіне түрленеді, биіктігі кіріс шама таңбасын сақтап сигналды түсіру моментіндегі кіріс шамасының мәнімен пропорционалды, бірақ импульстердің ұзақтығы жұмысшы интервалы (жұмыс істеу аралығы) деп аталады, өйткені осы уақыт аралығында импульстер орындаушы құрылғыға әсер етеді. Жұмыс істеу аралығында жүйе үздіксіз реттеу жүйелерінен еш айырмашылығы болмайды.

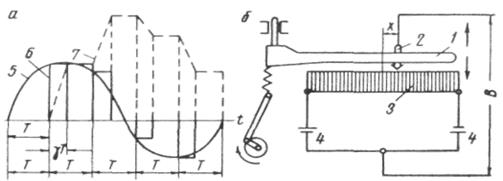
Бірінші типті импульстік үзбенің схемасы 9.4. сурет, 6- да келтірілген.

Түзу құлаушы имек 1 жоғары және төменге перодты қозғалыстар жасайды және жұмыс істеу аралығындағы сілтегішті 2 тұрақты уақыт аралығындағы 3 потенциометрдің сол немесе басқа нүктесіне қысады, потенциометрдің үштарына Э.Қ.К – і тең 4 батареялар қосылған. Берілген импульстік үзбенің кіріс шамасы болып потенциометрдің орта нүктесіне қатысты 2 сілтегіштің жылжуы болып табылады. Импульстік үзбенің шығыс шамасы импульстің ұзақтығына тең уақыттың бір бөлігіндегі кіріс шамасы қисығынан кесіп алынатын импульстерді береді. 9.4. сурет, 6 –ғы үзбенің шығыс шамасы тұрақты ұзақтықтың 6 (9.4, а сурет) кернеуінің импульстері болып табылады, бірақ олар шамасы мен таңбасы бойынша сілтегіштің жіберілетін имегінің қысылу моментіндегі орташа нүктесінен ауытқуына байланысты әртүрлі болып табылады.

Бірінші типті импульстік үзбедегі орындаушы қозғалтқыштың жылдамдығы әрбір жұмыс істеу аралығында түсіріп алудағы импульстік үзбенің кіріс шамасының мәніне пропорционалды өзгереді. Жылдамдыққа байланысты әрбір жұмыс аралығында орындаушы қозғалтқыштың жүру шамасы да өзгереді (7 график (сызба). Мұндағы екі көршілес импульстердің басынан арасындағы уақытты анықтайтын Т шамасы реттеу аралығы, немесе импульстердің кезектесуі деп аталады. Импульс ұзақтығы (жұмыс аралығы) арқылы белгіленеді. Коэффициент 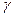импульстік үзбенің қуыстылығы деп аталады және өзінше жұмыс аралығының реттеу аралығына қатынасын береді, сонда 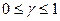болады.

Құлаушы имектің орнында жүйе реттеу тізбегінің бірдей уақыт аралығында периодты тұйықталады.

Екінші типке үздіксіз кіріс шамасы импульстер тізбегінде түрленеді, оның ұзақтығы түсіріп алу момент ішіндегі кіріс шамасының мәндеріне пропорционал, ал биіктігі кіріс шамасының таңбасын сақтап тұрақты күйде қалады (9.5, а сурет). Импульстік үзбе схемасы 9=5, б. Суретте келтірілген. Скошты құлаушы имек 4 жоғары және төменге қозғалады да, ортасында оқшауланған ажырамасы бар және Э.Қ.К. тең батареялармен 7 қосылған байланысты пластинкаға 6 жұмыс істеу аралығының уақыт ішіндегі 5 сілтегішті қысады. Үзбенің кіріс шамасы байланысты пластинаның орташа нүктесіне қатысты сілтегіштің x жылжуы болып табылады. Шығыс шамасы В болып тұрақты биіктік кернеуінің импульстер болып табылады, бірақ құлаушы имек қисайуына байланысты ұзақтығымен әртүрлі және сілтегіштің орташа нүктеге қатысты ауытқу бағыты бойынша әртүрлі.

Үшінші типтік үздіксіз кіріс шамасы тұрақты ұзақтығының биіктігі импульстер тізбегіне түрленеді, бірақ түсіріп алу моментіндегі кіріс шамасының таңбасына байланысты таңбалары әр түрлі.

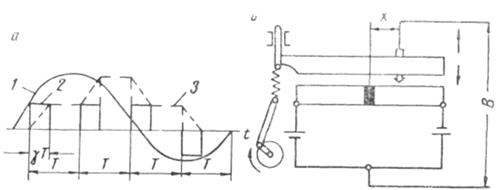
9.5. Сурет. Екінші типті импульстік үзбе

Бұл импульстік үзбе екінші типті үзбелерден ерекшелігі тек қана кесілген имектің орнына түзу имек қолданылады (9.6, б сурет).

Импульстік биіктігінің кіріс шаманың сәйкес ординатасына қатысты импульстік үзбенің күшею коэффициентін береді.

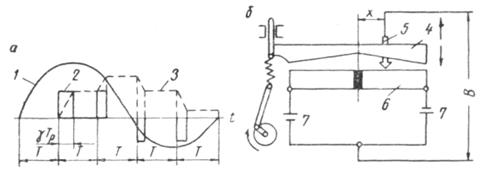
9.6. Сурет. Үшінші ретті импульстік үзбе

Егер импульстер бірінен – кейін бірі үздіксіз жүрген болса, яғни жұмыс аралығы Т реттеу аралығына тең, 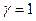сәйкес келеді, импульстік үзбе үздіксіз әрекет ететін жай күшейткіш үзбеге айналып кетеді.

Нөльге жақын ң біз кіші мәні кезінде импульстік үзбе ажыратқышқа айналады, ол реттеу тізбегін қысқа уақыт аралығына периодты түрде тұйықтайды. Мұндай ажыратқыштар үйкеліс күшінің қауіпті әсерін әлсіздендіру үшін жасанды вибрациялы автоматты реттеу жүйесінің схемаларында қолданылады. Баяу өзгеретін процестерді ретеу үшін алдымен екінші мен үшінші типті жүйелер қолданылады. Бірінші типті жүйелер өлшеу және радиолокациялы техникада қолданылады.

Автоматты реттеу импульсті жүйелеріндегі өтпелі процестерді зерттеу үшін қарапайым сызықты дифференциалды теңдеу аппараты жарамсыз. Бұл зерттеулер графоаналитикалық немесе Лапластың дискретті түрлендіруінің көмегімен әртүрі теңдеулерді пайдаланып жүргізіледі. Алдыңғы екі әдіс өте қиын және іс жүзінде сирек қолданылады.

Лапластың дискреттік түрлендіруінің екі түрі белгілі – қарапайым дискреттік түрлендіру және соңғы жылдары аса кеңінен пайдаланып келе жатқан z – түрлендіру, өйткені өрнектер аса қарапайым түрде алынады.