Расчет цепей при смешанном соединении элементов

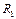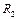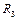На рис.9 приведена цепь при смешанном соединении линейного сопротивления и двух нелинейных и ВАХ которых приведены на рис.10. Требуется определить установившиеся значения токов 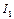, , 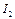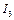и напряжений на элементах при заданной ЭДС .

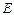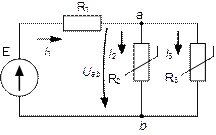
Рис.9. Цепь со смешанным соединением элементов

Сначала находим ВАХ параллельного участка 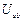путем сложения абсцисс 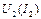и 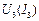при одинаковых напряжениях. Далее складывая ординаты характеристик 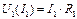и 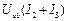, находим результирующую ВАХ всей цепи 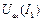. Порядок построения показан на рис.10 стрелками.

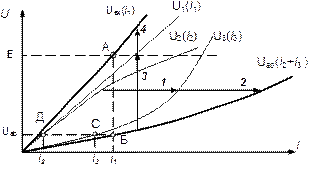
Рис.10. Расчет цепи при смешанном соединении

Пересечения последней кривой с линией Е – точка А, позволяет определить ток 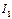и напряжения 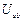на параллельном участке. Пересечение линии напряжения 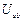с кривым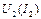и и 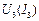определяет токи ветвей , .

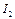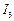Преобразование активных нелинейных двухполюсников

Рассмотрим цепь с последовательно соединенными нелинейным сопротивлением 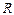с Э.Д.С. постоянного тока 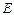(рис.11).

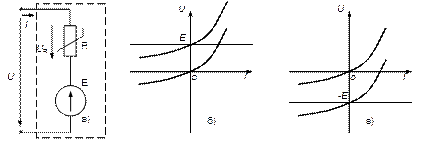
Рис. 11. Преобразование двухполюсников

а) активный двухполюсник с ЭДС; б,в) построение ВАХ двухполюсника

На основании второго закона Кирхгофа имеем:

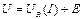, (6)

Из последнего уравнения следует, что ВАХ рассматриваемой цепи может быть получена суммированием ординат 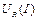и ЭДС 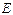, т.е. путем смещения ВАХ на 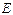вверх по ординате, если 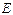>0 и вниз если 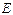<0 (рис.11.б, в).

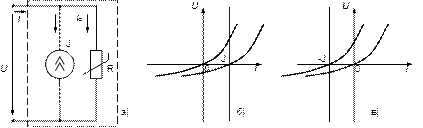
Рис. 12. Преобразование двухполюсников

а) активный двухполюсник с источником тока;

б,в) построение ВАХ двухполюсника

ВАХ активного двухполюсника, представляющее собой параллельное соединение нелинейного сопротивления 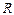и источника постоянного тока 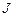, получается путем смещения ВАХ нелинейного элемента 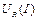вдоль оси тока на 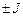(рис.12.б,в).

Преобразованием двухполюсников пользуются не только для решения прямой задачи, но и для решения обратной задачи: заменить нелинейный двухполюсник, ВАХ которого не проходит через начало координат, нелинейным сопротивлением и идеализированным источником постоянного тока.

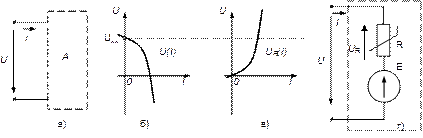
Рис.13. К решению обратной задачи

а) активный двухполюсник; б) ВАХ двухполюсника; в) ВАХ нелинейного сопротивления; г) схема замещения двухполюсника.

Покажем это на конкретном примере. Пусть активный двухполюсник (рис.13.а) имеет ВАХ, показанную на рис.13.б. Представим двухполюсник схемой замещения на рис.13.г. Из выражения (6) следует:

.

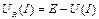Для нелинейного сопротивления 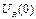=0, получим 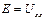, тогда можно записать:

.

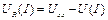ВАХ нелинейного сопротивления получается путем вычитания 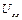из ординат ВАХ двухполюсника 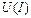. В итоге получаем ВАХ нелинейного сопротивления 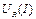на рис.13.в.