Геометрический смысл энергетического условия пластичности

Условие пластичности

Отыскание напряженного состояния в точке тела без учета свойств этого тела еще не позволяет судить о наличии пластического формоизменения. Учитывать свойства материала пластически деформируемого тела можно при помощи физических уравнений, а именно уравнения пластичности определяющего условие перехода материала из упругого состояния в пластическое или условие предельного состояния.

При одноосном растяжении пластическое состояние наступает, когда нормальное напряжение достигает предела текучести

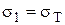
При объемном напряженном состоянии, наиболее часто встречающимся в процессах ОМД, начало пластического течения будет при определенном соотношении между 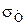и главными нормальными напряжениями.

Согласно гипотезе Сен-Венана-Треска пластическая деформация наступает тогда, когда одно из главных касательных напряжений достигнет половины предела текучести независимо от схемы напряженного состояния, т.е. когда .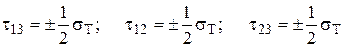

При , .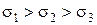

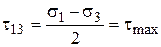Тогда 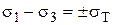(при главных напряжениях одного знака)

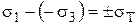или

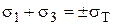(при главных напряжениях разного знака)

Два других 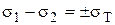, 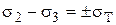уравнения также справедливыы. Здесь (+) – растяжение, (-) – сжатие.

Однако условие максимального касательного напряжения не учитывает влияния третьего главного напряжения .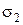

Губер, Мизес, а позднее Генки сформулировали другое (энергетическое) условие пластичности, которое трактуется так: пластическая деформация начинается тогда, когда потенциальная энергия упругого изменения формы достигнет определенной величины, независимо от вида напряженного состояния.

Полная потенциальная энергия деформации

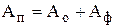(1)

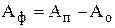
где 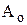- потенциальная энергия упругого изменения объема;

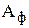- потенциальная энергия упругого изменения формы.

Из теории упругости известно

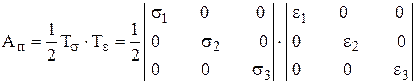или

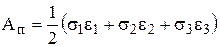. (2)

В свою очередь

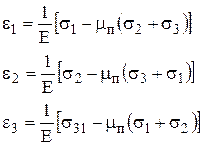
где 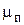- коэффициент Пуассона, выражающий отношение поперечной деформации к продольной ;

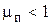Е – модуль упругости 1-го рода (размерность напряжений).

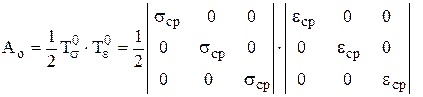или

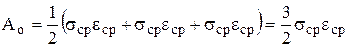, (3)

где .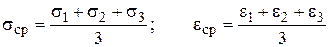

Подставляя значения 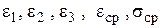соответственно в (2) и (3) и далее полученные значения 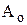и 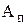в (1), запишем

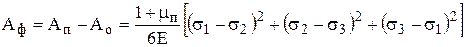
При линейном напряженном состоянии 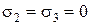пластическая деформация наступит когда 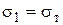. Тогда .

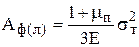Поскольку сформулированное условие пластичности не зависит от вида напряженного состояния .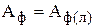

Тогда

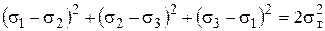(4)

Выразив через главные касательные напряжения, запишем

.

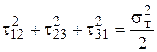В произвольных осях координат

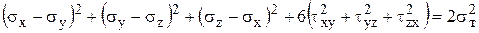
Учитывая, что

,

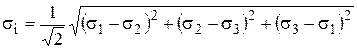легко установить

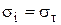
Пластическая деформация наступит тогда, когда интенсивность напряжений достигнет величины, равной пределу текучести.

Таким образом условие пластичности Губера-Мизеса-Генки называют условием постоянства интенсивности напряжений.

Учитывая, что

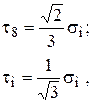
можно записать, что пластическая деформация наступит при

.

Здесь k– сопротивление металла пластическому сдвигу или пластическая постоянная, т.е. максимальная величина, которой может достичь главное касательное напряжение при пластической деформации.

.

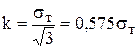Откуда 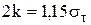- обычно называемая вынужденным пределом текучести.

Записанные уравнения пластичности пригодны лишь для идеально-пластических сред, т.е. неупрочняемых, в то время как в большинстве случаев деформация протекает с упрочнением. Учет этого обстоятельства сводится к тому, что вместо предела текучести 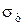необходимо использовать другую характеристику материала 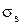- напряжение текучести. Тогда выражение (4) можно записать

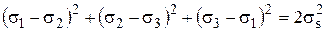
Геометрический смысл энергетического условия пластичности

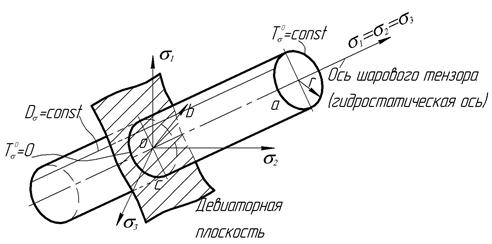
Он становится очевидным, если в уравнении (40 рассматривать напряжения 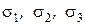как текущие координаты. В этих координатах уравнение (4) представляет собой поверхность неограниченного по длине кругового цилиндра радиусом 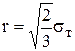с осью, равнонаклоненной к осям координат под углом, косинус которого равен .

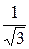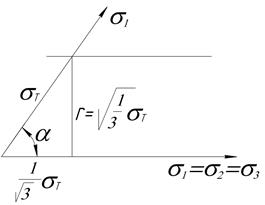При линейном напряженном состоянии 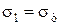a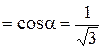

т.к.

Если комбинации главных напряжений в деформируемом элементе отвечают точке (в), лежащей на поверхности цилиндра, то этот элемент находится в пластическом состоянии, а точке, лежащей внутри цилиндра отвечает упругое состояние элемента. Окружность на поверхности цилиндра от пересечения его с плоскостью, перпендикулярной гидростатической оси, представляет геометрическое место точек напряженных состояний с одинаковым шаровым тензором .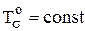

Плоскость, проходящая через начало координат и ортогональная гидростатической, оси называется девиаторной и на окружности С поэтому . Образующая цилиндра, например, (в) является геометрическим местом точек, для которых разности главных напряжений одинаковы, т.е. 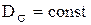. Геометрическая интерпретация условия Треска-Сен-Венана представляет собой правильную шестигранную призму, вписанную в цилиндр.