Техническое обслуживание систем по состоянию с периодическим контролем

При решении задачи будем предполагать, что техническое состояние изделия определяется численными значениями специально выбранных контролируе­мых параметров. Пусть далее η(t)—монотонная случайная функция времени t, соответствующая контролируемому параметру изделия, η**—предельно допустимое значение параметра, пересечение которого реализациями случайного процесса приводит к отказам изделия, а η* — наименьшее предотказовое значение параметра, такое, что интер­вал Δη = η** - η* определяет упреждающий допуск (рис.4.5). Область 0, η* изменения случайной функции будем называть исправ­ным состоянием изделия (состояние 1), область (η*, η**) изменения
η(t) будем называть состоянием профилактических замен (состояние 2), а область( η **,∞)— неработоспособным (состояние 3).

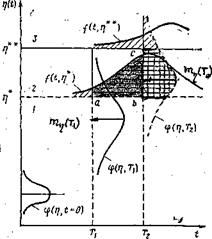
Рис.4.5 Связь периодичности проверок (τ = Т₂-Т₁) с упреждающим допуском Δη = η **- η *на диагностиче­ский параметр (модель экранов).

Примем следующие допущения относительно случайной функции η(t). Прежде всего пусть Р {0 < η (0)< η*}=1, т.е. изделие, имею­щее наработку t = 0, находится в исправном состоянии с вероятно­стью «единица». В момент t = Т случайный процесс η(t) соответствует исправному состоянию с вероятностью Р₁ = Р {0 < η (Т) < η}, состоянию профилактических замен с вероятностью P₂ = Р (η < η(T)< η **} и неработоспособному состоянию с вероятностью Р₃ = Р{η**< η(Т) < ∞}. Таким образом, распределение процесса по состояниям изделия подчиняется условию нормирования, Р₁ + Р₂ + Р₃ = 1. Предполагается также, что при замене устанавливается новое изделие или отремонтированное, причем последнее по своему техническому состоянию эквивалентно новому. В дальнейшем рассмотрим вопросы оценки момента первой проверки Т₁ и упреждающего допуска Δη [16].

Оценка момента первой проверки.

Очевидно надежность системы равна

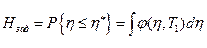
или

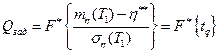
Отсюда

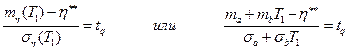
Таким образом

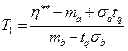
Оценка упреждающего допуска.

Условие безотказности системы на интервале обслуживания определяется равенством

где 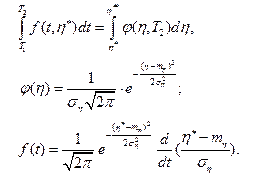(4.31)

Выполнение условия (4.31) обеспечивает такое расположение 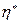, при котором все траектории процесса, прошедшие через горизонтальный участок (a , b ) попадают на вертикальный участок ( b , c )(см. рис. 4.5, 4.6 ).

В дальнейшем оценим первый интеграл соотношения (4.31)

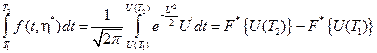
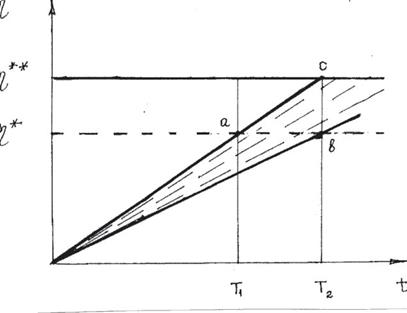
Рис.4. 6 Оценка 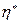для веерной функции .

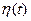Производя линеаризацию F^*{U} в окрестности нуля (см. рис.4.7), приближенно получим

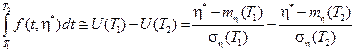
F^*(U)

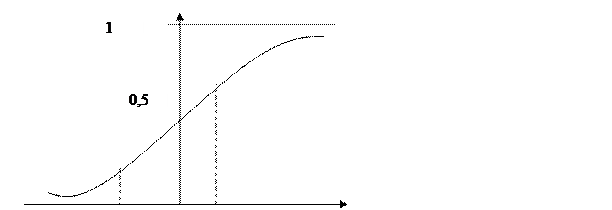
U(T₂) 0 U(T₁) U

Рис.4 7 Функция нормированного нормального распределения

Соответственно для второго интеграла найдем

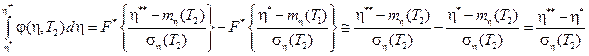
Приравнивая интегралы между собой, получим

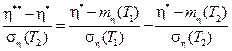
После преобразований имеем

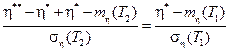
Отсюда

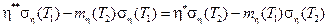(4 3.2 )

Таким образом

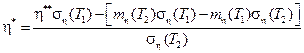(4.33 )

В случае линейной зависимости

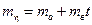
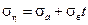(4 .34 )

выражение в квадратных скобках в соотношении (4.3) будет равно

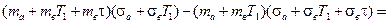
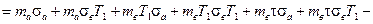
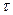
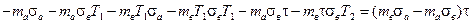(4. 35 )

Таким образом, выражение для η^* примет вид

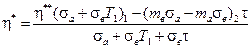(4 .36 )

Соответственно

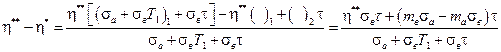(4. 37 )

Соотношения (4.36) и (4.37) позволяют оценивать периодичность обслуживания 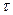в зависимости от величины упреждающего допуска .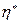