Уравнение первого закона термодинамики для потока
Под открытыми понимаются термодинамические системы, которые кроме обмена теплотой и работой с окружающей средой допускают также и обмен массой. В технике широко используются процессы преобразования энергии в потоке, когда рабочее тело перемещается из области с одними параметрами в область с другими. Это, например, расширение пара в турбинах, сжатие газов в компрессорах.
Будем рассматривать лишь одномерные стационарные потоки, в которых параметры зависят только от одной координаты, совпадающей с направлением вектора скорости, и не зависят от времени. Условие неразрывности течения в таких потоках заключается в одинаковости массового расхода m рабочего тела в любом сечении:
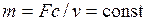 ,
,
где F — площадь поперечного сечения канала; с — скорость рабочего тела.
Рассмотрим термодинамическую систему, представленную схематически на рисунке 7.1.
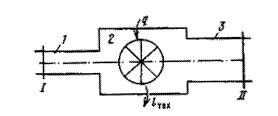
Рисунок 7.1 - Открытая термодинамическая система
По трубопроводу 1 рабочее тело с параметрами Т1 , p1, v1 подается со скоростью c1в тепломеханический агрегат 2 (двигатель, паровой котел, компрессор и т. д.). Здесь каждый килограмм рабочего тела в общем случае может получать от внешнего источника теплоту q и совершать техническую работу lтех, например, приводя в движение ротор турбины, а затем удаляется через выхлопной патрубок со скоростью с2, имея параметры Т2 , p2, v2.
Если в потоке мысленно выделить замкнутый объем рабочего тела и наблюдать за изменением его параметров в процессе перемещения, то для описания его поведения будут пригодны все полученные выше термодинамические соотношения и, в частности, первый закон термодинамики в обычной записи: 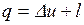 .
.
Внутренняя энергия есть функция состояния рабочего тела, поэтому значение определяется параметрами рабочего тела при входе (сечение потока I), а значение — параметрами рабочего тела при выходе из агрегата (сечение II).
Работа расширения l совершается рабочим телом на поверхностях, ограничивающих выделенный движущийся объем, т. е. на стенках агрегата и границах, выделяющих этот объем в потоке. Часть стенок агрегата неподвижна, и работа расширения на них равна нулю. Другая часть стенок специально делается подвижной (рабочие лопатки в турбине и компрессоре, поршень в поршневой машине), и рабочее тело совершает на них техническую работу 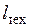
При входе рабочее тело вталкивается в агрегат. Для этого нужно преодолеть давление p1. Поскольку p1=const, то каждый килограмм рабочего тела может занять объем лишь при затрате работы, равной 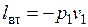 .
.
Для того чтобы выйти в трубопровод 3, рабочее тело должно вытолкнуть из него такое же количество рабочего тела, ранее находившегося в нем, преодолев давление р2, т. е. каждый килограмм, занимая объем v2 должен произвести определенную работу выталкивания 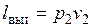 .
.
Сумма 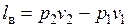 называется работой вытеснения.
называется работой вытеснения.
Если скорость на выходе больше, чем на входе, то часть работы расширения будет затрачена на увеличение кинетической энергии рабочего тела в потоке, равное 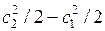 .
.
Наконец, в неравновесном процессе некоторая работа может быть затрачена на преодоление сил трения. Окончательно
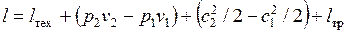 .
.
Теплота, сообщенная каждому килограмму рабочего тела во время прохождения его через агрегат, складывается из теплоты 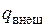 , подведенной снаружи, и теплоты
, подведенной снаружи, и теплоты 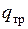 , в которую переходит работа трения внутри агрегата, т. е.
, в которую переходит работа трения внутри агрегата, т. е. 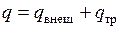 .
.
Подставив полученные значения q и l в уравнение первого закона термодинамики, получим
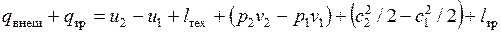 .
.
Поскольку теплота трения равна работе трения, окончательно запишем:
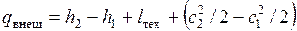 .
.
Это и есть выражение первого закона термодинамики для потока, который можно сформулировать так: теплота, подведенная к потоку рабочего тела извне, расходуется на увеличение энтальпии рабочего тела, производство технической работы и увеличение кинетической энергии потока.
В дифференциальной форме уравнение записывается в виде
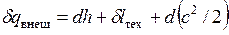 . (7.1)
. (7.1)
Оно справедливо как для равновесных процессов, так и для течений, сопровождающихся трением.
Выше было указано, что к замкнутому объему рабочего тела, выделенному в потоке, применимо выражение первого закона термодинамики для закрытой системы, т.е. 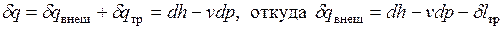 .
.
Сравнивая это выражение с уравнением *, получим:
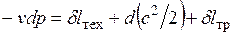 , или
, или
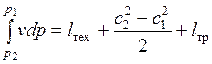 .
.
Величину 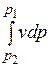 называют располагаемой работой. В p, v-диаграмме она изображается заштрихованной площадью.
называют располагаемой работой. В p, v-диаграмме она изображается заштрихованной площадью.
Применим первый закон термодинамики к различным типам тепломеханического оборудования.
Теплообменный аппарат(устройство, в котором теплота от жидкой или газообразной среды передается другой среде). Для него 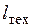 =0, a
=0, a 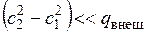 , поэтому
, поэтому
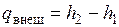 .
.
Следует подчеркнуть, что для теплообменника, установленного в потоке, это выражение справедливо не только в изобарном процессе, но и в процессе с трением, когда давление среды уменьшается из-за сопротивления.
Тепловой двигатель.Обычно 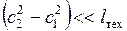 , поэтому рабочее тело производит техническую работу за счет уменьшения энтальпии:
, поэтому рабочее тело производит техническую работу за счет уменьшения энтальпии:
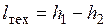 . (7.2)
. (7.2)
Величину 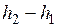 называют располагаемым теплоперепадом.
называют располагаемым теплоперепадом.
Интегрируя уравнение 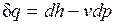 от p1 до p2 и от h1до h2для случая, когда
от p1 до p2 и от h1до h2для случая, когда 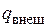 =0, получим
=0, получим
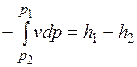 . (7.3)
. (7.3)
Сравнивая выражения (7.2) и (7.3), приходим к выводу, что
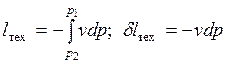 .
.
Таким образом, при 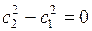 ,
, 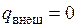 и отсутствии потерь на трение получаемая от двигателя техническая работа равна располагаемой, т. е. тоже изображается заштрихованной площадью на рисунке 7.2.
и отсутствии потерь на трение получаемая от двигателя техническая работа равна располагаемой, т. е. тоже изображается заштрихованной площадью на рисунке 7.2.
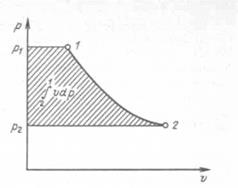
Рисунок 7.2 - Изображение располагаемой и технической работы в координатах p, v
Компрессор.Если процесс сжатия газа в компрессоре происходит без теплообмена с окружающей средой ( 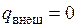 ) и c1=c2, что всегда можно обеспечить надлежащим выбором сечений всасывающего и нагнетательного воздухопроводов, то
) и c1=c2, что всегда можно обеспечить надлежащим выбором сечений всасывающего и нагнетательного воздухопроводов, то
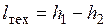
В отличие от предыдущего случая здесь h1<h2, т.е. техническая работа в адиабатном компрессоре затрачивается на увеличение энтальпии газа.
Сопла и диффузоры.Специально спрофилированные каналы для разгона рабочей среды и придания потоку определенного направления называются соплами. Каналы, предназначенные для торможения потока и повышения давления, называются диффузорами. Техническая работа в них не совершается, поэтому уравнение 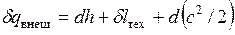 приводится к виду
приводится к виду
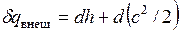 .
.
С другой стороны, для объема рабочего тела, движущегося в потоке без трения, применимо выражение первого закона термодинамики для закрытой системы 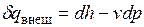 .
.
Приравняв правые части двух последних уравнений, получим
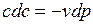 . (7.4)
. (7.4)
 Видно, что dc и dp всегда имеют противоположные знаки. Следовательно, увеличение скорости течения в канале (dc>0) возможно лишь при уменьшении давления в нем (dp<0). Наоборот, торможение потока (dc<0) сопровождается увеличением давления (dp>0),
Видно, что dc и dp всегда имеют противоположные знаки. Следовательно, увеличение скорости течения в канале (dc>0) возможно лишь при уменьшении давления в нем (dp<0). Наоборот, торможение потока (dc<0) сопровождается увеличением давления (dp>0),
Так как длина сопла и диффузора невелика, а скорость течения среды в них достаточно высока, то теплообмен между стенками канала и средой при малом времени их контакта настолько незначителен, что в большинстве случаев им можно пренебречь и считать процесс истечения адиабатным ( 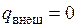 ). При этом уравнение
). При этом уравнение 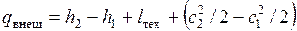 принимает вид
принимает вид
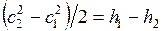 . (7.5)
. (7.5)
Следовательно, ускорение адиабатного потока происходит за счет уменьшения энтальпии, а торможение потока вызывает ее увеличение.
Проинтегрировав соотношение (7.4) и сравнив его с уравнением (7.5), получим, что для равновесного адиабатного потока
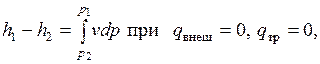
т. е. располагаемая работа при адиабатном расширении равна располагаемому теплоперепаду.
