Равнобочная гипербола (Равносторонняя гипербола) – гипербола, действительная и мнимая оси которой равны

Радиус окружности – расстояние между центром и любой точкой этой окружности.

Собственный вектор – ненулевой вектор-столбец r, удовлетворяющий уравнению Ar = lr, где A - матрица квадратичной формы, l - некоторое число.

Собственное число (Собственное значение) – число l, удовлетворяющее уравнению Ar = lr, где A - матрица квадратичной формы, r - некоторый ненулевой вектор-столбец.

Текущие координаты – координаты (x, y) переменной точки линии на плоскости или координаты (x, y, z) переменной точки поверхности в пространстве.

Уравнение линии(кривой) в декартовой прямоугольной системе координат на плоскости – уравнение с двумя переменными F(x, y) = 0, которому удовлетворяют координаты x и y каждой точки, лежащей на этой линии, и не удовлетворяют координаты никакой точки, не лежащей на ней.

Фокальный радиус – расстояние точки кривой второго порядка до фокуса.

Фокус – точка, лежащая в плоскости кривой второго порядка и обладающая соответствующим фокальным свойством этой кривой.

Фокусное расстояние (Фокальное расстояние) – расстояние между фокусами эллипса или гиперболы.

Характеристическое уравнение – уравнение |A – lE| = 0, где A - матрица квадратичной формы, E - единичная матрица; корни характеристического уравнения l₁ и l₂ являются собственными числами квадратичной формы.

Центр симметрии – точка плоскости или пространства, при повороте вокруг которой на некоторый угол геометрическая фигура совмещается сама с собой.

Центральная кривая второго порядка - кривая второго порядка, имеющая центр симметрии; такими кривыми являются окружность, эллипс, гипербола.

Эксцентриситет – число, определяющее вид кривой второго порядка.

Обозначение: e, e.

Эксцентриситет гиперболы– число, равное отношению фокусного расстояния к действительной оси: e = c/a. Пояснение. Эксцентриситет гиперболы являющееся мерой ее “сплющенности”.

Эксцентриситет эллипса – число, равное отношению фокусного расстояния к большой оси: e = c/a. Пояснение. Эксцентриситет эллипса являющееся мерой его “сплющенности”; при e = 0 эллипс представляет собой окружность.

Эллипс - алгебраическая кривая второго порядка, каноническое уравнение которой в декартовых координатах имеет вид: 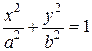.