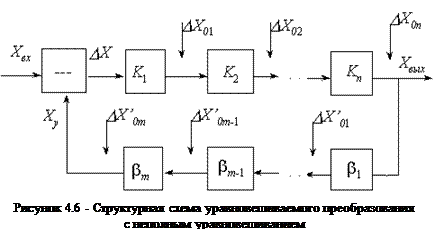
Структурная схема уравновешенного преобразования
Особенность схемы (рис. 4.6) состоит в том, что выходная величина 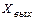 подвергается обратному преобразованию в величину
подвергается обратному преобразованию в величину 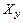 , однородную с входной величиной
, однородную с входной величиной 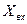 и почти полностью уравновешивает её, в результате чего на вход цепи прямого преобразования поступает только небольшая часть
и почти полностью уравновешивает её, в результате чего на вход цепи прямого преобразования поступает только небольшая часть 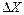 преобразуемой величины
преобразуемой величины 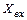 . Другими словами, используется отрицательная обратная связь.
. Другими словами, используется отрицательная обратная связь.
Возможны два режима работы схемы: режим неполного уравновешивания и режим полного уравновешивания.
1. Режим неполного уравновешивания.
В этом режиме входная 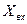 и уравновешивающая
и уравновешивающая 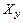 величины образуют разность
величины образуют разность 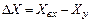 .
.
 |
Уравнение цепей прямого и обратного преобразования будут иметь вид, соответственно 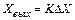 и
и 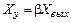 , где
, где 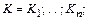
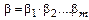 . Отсюда имеем
. Отсюда имеем
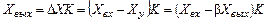 . (4.22)
. (4.22)
Производя перегруппировку, получаем 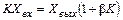 или
или
 . (4.23)
. (4.23)
Коэффициент преобразования уравновешивающего СИ будет равен
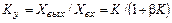 . (4.24)
. (4.24)
При 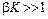
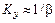 , т.е. цепь прямого преобразования слабо влияет на работу прибора, однако его чувствительность падает в (1+
, т.е. цепь прямого преобразования слабо влияет на работу прибора, однако его чувствительность падает в (1+ 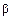 K) раз.
K) раз.
Определим относительную погрешность, обусловленную нестабильностью коэффициентов преобразования 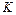 и
и 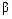 для этой схемы. Для этого продифференцируем выражение (4.23) по
для этой схемы. Для этого продифференцируем выражение (4.23) по 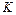 и
и 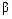
 (4.25)
(4.25)
и деля его на 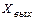 , получаем
, получаем
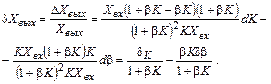 (4.26)
(4.26)
Таким образом, относительная погрешность состоит из суммы двух членов, один из которых пропорционален суммарной погрешности всех преобразователей цепи прямого преобразования, а другой – суммарной погрешности преобразования цепи обратной связи. Причем погрешность от нестабильности цепи 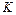 уменьшается в
уменьшается в 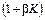 раз, а погрешность, обусловленная нестабильностью цепи обратной связи, почти полностью входит в суммарную погрешность. Действительно, при
раз, а погрешность, обусловленная нестабильностью цепи обратной связи, почти полностью входит в суммарную погрешность. Действительно, при 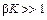
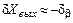 . Следовательно, в прямой цепи можно использовать нестабильные преобразователи, необходимо только, чтобы
. Следовательно, в прямой цепи можно использовать нестабильные преобразователи, необходимо только, чтобы 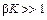 и коэффициент обратного преобразования имел высокую стабильность. Необходимо учитывать, что введением обратного преобразования в
и коэффициент обратного преобразования имел высокую стабильность. Необходимо учитывать, что введением обратного преобразования в 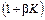 раз уменьшается чувствительность измерительного устройства. Для её сохранения коэффициент
раз уменьшается чувствительность измерительного устройства. Для её сохранения коэффициент 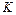 нужно увеличить в
нужно увеличить в 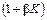 раз. При этом могут возникнуть условия для самовозбуждения СИТ. Поэтому предел увеличения
раз. При этом могут возникнуть условия для самовозбуждения СИТ. Поэтому предел увеличения 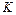 определяется динамической устойчивостью прибора.
определяется динамической устойчивостью прибора.
Необходимо отметить, что нелинейность функции прямого преобразования можно рассматривать как изменение коэффициента преобразования 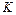 относительно номинального значения.
относительно номинального значения.
Это изменение может быть вызвано и другими причинами: вариацией параметров окружающей среды (температуры, давления, влажности), инерционностью звеньев, механическими воздействиями (вибрацией, тряской) и т.п. Введение обратного преобразования одинаково уменьшает влияние всех вышеперечисленных причин.
Оценим погрешность, обусловленную дрейфом нуля, наводками и т.п. Для этого введем в схему дополнительные сигналы 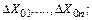
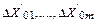 . Приводя эти сигналы к входу схемы, получаем
. Приводя эти сигналы к входу схемы, получаем
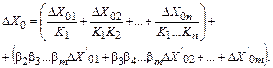 (4.27)
(4.27)
Из этого выражения видно, что аддитивная погрешность не зависит от глубины обратной связи и не может быть уменьшена по абсолютной величине введением схемы уравновешивающего преобразования.
Наибольшее требование по минимальному дрейфу нуля предъявляется к первому прямому и первому обратному преобразователю.
