Індивідуальні завдання за темою
«лінійна та векторна алгебра»
Завдання 1
„Лінійна алгебра”
Задані матриці 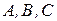 . Необхідно:
. Необхідно:
1. Знайти величину визначника матриці 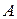 наступними способами:
наступними способами:
а) використавши правило трикутника (правило Саррюса);
б) розклавши визначник за елементами того ряда, який містить нуль;
в) одержавши 2 нулі в деякому ряді та розклавши за його елементами визначник.
2. Знайти матрицю 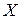 , якщо
, якщо 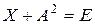 , де
, де 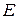 – одинична матриця.
– одинична матриця.
3. Знайти два можливі добутки, утворені з матриць 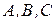 .
.
4. Знайти матрицю 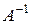 , обернену до матриці
, обернену до матриці 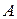 .
.
| 1.1 | 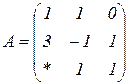 | 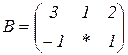 | 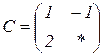 |
| 1.2 | 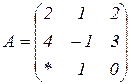 | 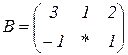 | 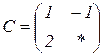 |
| 1.3 | 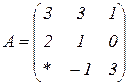 | 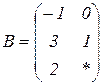 | 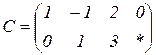 |
| 1.4 | 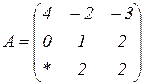 | 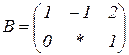 | 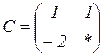 |
| 1.5 | 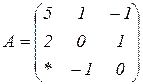 | 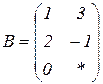 | 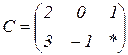 |
| 1.6 | 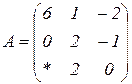 | 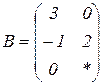 | 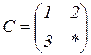 |
| 1.7 | 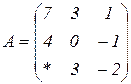 | 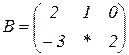 | 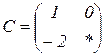 |
| 1.8 | 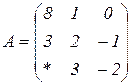 | 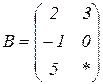 | 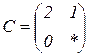 |
Продовження
| 1.9 | 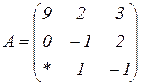 | 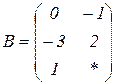 | 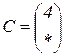 |
| 1.10 | 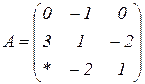 | 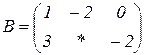 | 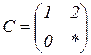 |
| 1.11 | 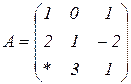 |  | 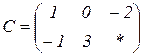 |
| 1.12 | 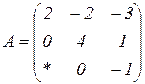 |  | 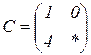 |
| 1.13 | 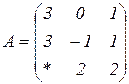 | 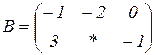 | 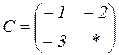 |
| 1.14 | 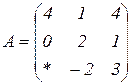 | 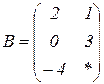 | 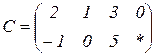 |
| 1.15 | 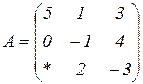 | 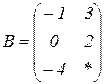 | 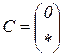 |
| 1.16 | 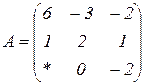 | 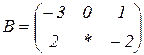 | 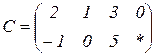 |
| 1.17 | 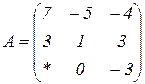 | 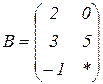 | 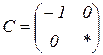 |
| 1.18 | 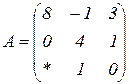 | 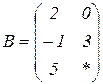 | 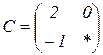 |
Продовження
| 1.19 | 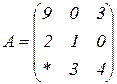 | 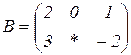 |  |
| 1.20 | 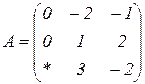 | 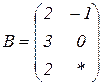 | 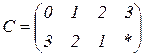 |
| 1.21 | 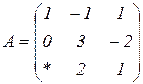 | 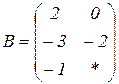 | 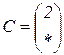 |
| 1.22 | 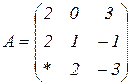 | 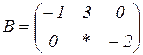 | 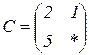 |
| 1.23 | 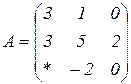 | 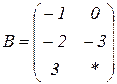 | 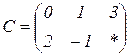 |
| 1.24 | 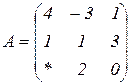 | 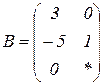 | 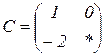 |
| 1.25 |  | 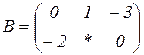 | 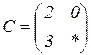 |
| 1.26 | 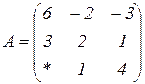 | 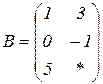 | 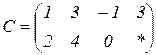 |
| 1.27 | 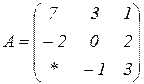 | 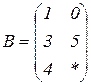 | 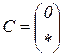 |
| 1.28 | 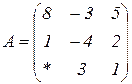 | 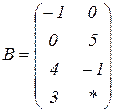 | 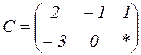 |
Продовження
| 1.29 | 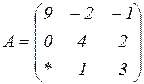 | 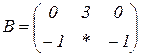 | 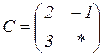 |
| 1.30 | 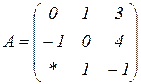 | 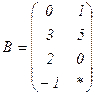 |  |
Завдання 2
„Лінійна алгебра”
Знайти величину визначника четвертого порядку, скориставшись його властивостями та одержавши три нулі в будь-якому рядку.
2.1 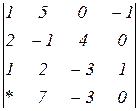 | 2.2 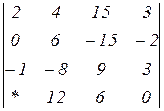 | 2.3 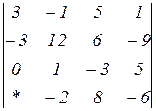 |
2.4 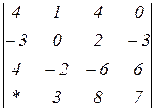 | 2.5 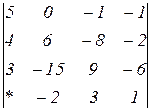 | 2.6  |
2.7 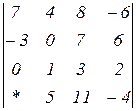 | 2.8 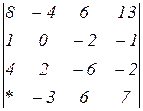 | 2.9 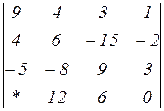 |
2.10 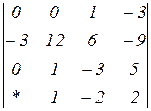 | 2.11 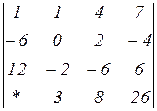 | 2.12 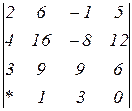 |
2.13 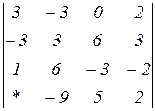 | 2.14 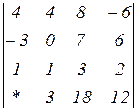 | 2.15 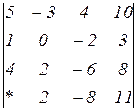 |
Продовження
2.16 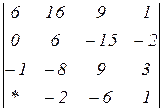 | 2.17 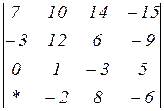 | 2.18 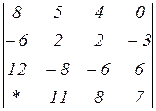 |
2.19 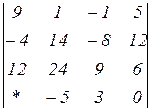 | 2.20 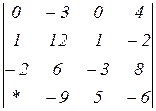 | 2.21 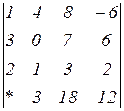 |
2.22 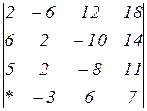 | 2.23 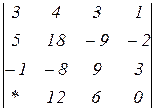 | 2.24 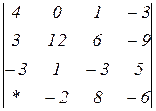 |
2.25  | 2.26 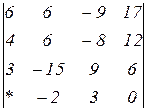 | 2.27 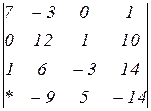 |
2.28 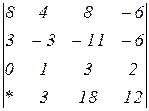 | 2.29 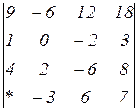 | 2.30 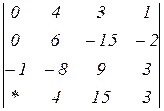 |
Завдання 3
„Лінійна алгебра”
Розв’язати систему лінійних алгебраїчних рівнянь трьома способами:
а) за формулами Крамера;
б) методом Гаусса;
в) методом оберненої матриці.
3.1 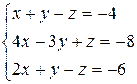 | 3.2 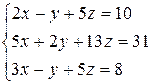 | 3.3 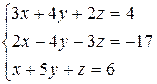 |
3.4 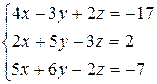 | 3.5 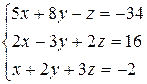 | 3.6 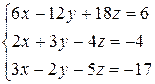 |
3.7 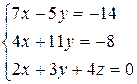 | 3.8  | 3.9 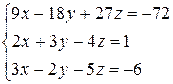 |
3.10 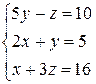 | 3.11 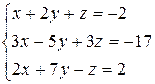 | 3.12 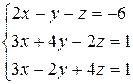 |
3.13 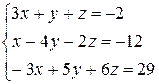 | 3.14 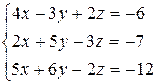 | 3.15 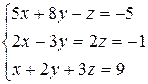 |
3.16 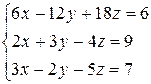 | 3.17 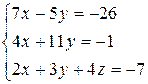 | 3.18 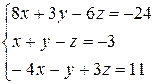 |
Продовження
3.19 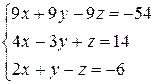 | 3.20 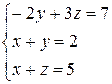 | 3.21 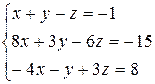 |
3.22 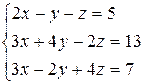 | 3.23 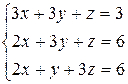 | 3.24 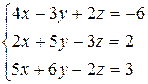 |
3.25 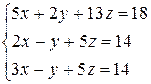 | 3.26 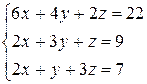 | 3.27 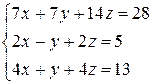 |
3.28  | 3.29 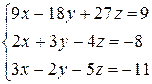 | 3.30 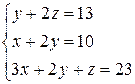 |
Завдання 4
„Векторна алгебра”
Дані координати точок 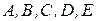 . Необхідно:
. Необхідно:
1. Знайти модуль та напрямок вектора 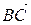 у просторі.
у просторі.
2. Знайти кут між векторами 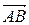 та
та 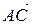 .
.
3. Знайти проекцію вектора  на напрям вектора
на напрям вектора 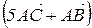 .
.
4. Знайти вектор 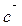 , перпендикулярний до вектора
, перпендикулярний до вектора 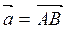 і до
і до 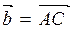 .
.
5. Обчислити площу трикутника АВС.
6. Знайти висоту паралелограма, побудованого на векторах 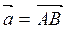 і
і 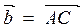 .
.
7. Обчислити об’єм піраміди 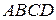 .
.
8. Перевірити, чи колінеарні вектори 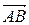 і
і 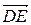 .
.
9. Перевірити, чи ортогональні вектори 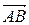 і
і 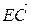 .
.
10. Перевірити, чи належать точки 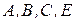 до однієї площини.
до однієї площини.
| 4.1 | 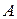 (1; –1; *) (1; –1; *) | 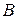 (1; 2; 1) (1; 2; 1) | 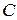 (–3; 2; *) (–3; 2; *) | 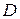 (0; 0; –1) (0; 0; –1) | 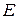 (2; 6; *) (2; 6; *) |
| 4.2 | 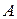 (2; 3; *) (2; 3; *) | 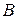 (2; 1; –1) (2; 1; –1) | 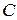 (3; –1; *) (3; –1; *) | 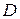 (1; –1; 3) (1; –1; 3) | 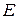 (5; 2; *) (5; 2; *) |
| 4.3 | 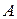 (3; 3; *) (3; 3; *) | 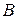 (2; –1; 3) (2; –1; 3) | 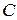 (0; 2; *) (0; 2; *) | 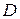 (0; 1; 3) (0; 1; 3) | 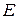 (1; –1; *) (1; –1; *) |
| 4.4 | 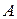 (4; 2; *) (4; 2; *) | 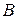 (–1; 3; 0) (–1; 3; 0) | 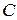 (0; –1; *) (0; –1; *) | 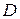 (–2;1;–1) (–2;1;–1) | 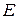 (5; 2; *) (5; 2; *) |
| 4.5 | 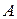 (5; –2; *) (5; –2; *) | 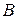 (–2; –1;3) (–2; –1;3) | 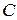 (1; –2; *) (1; –2; *) | 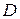 (–1; 0; 1) (–1; 0; 1) | 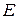 (7;–2; *) (7;–2; *) |
| 4.6 | 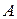 (6; 0; *) (6; 0; *) | 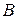 (1; –2; 0) (1; –2; 0) | 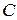 (0; 1; *) (0; 1; *) | 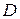 (2; 0; –3) (2; 0; –3) | 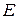 (–1; 1; *) (–1; 1; *) |
| 4.7 | 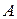 (7; 1; *) (7; 1; *) | 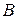 (2; 2; –1) (2; 2; –1) | 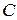 (–1; –1; *) (–1; –1; *) | 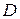 (–1;–1;0) (–1;–1;0) | 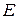 (5; 2; *) (5; 2; *) |
| 4.8 | 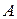 (8; 1; *) (8; 1; *) | 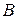 (2; –1; 0) (2; –1; 0) | 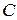 (2; 1; *) (2; 1; *) | 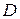 (2; 1; 3) (2; 1; 3) | 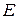 (4; 0; *) (4; 0; *) |
| 4.9 | 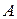 (9; 2; *) (9; 2; *) | 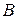 (1; –1; 1) (1; –1; 1) | 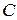 (2; 0; *) (2; 0; *) | 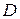 (2; 0; –1) (2; 0; –1) | 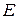 (6; 6; *) (6; 6; *) |
| 4.10 | 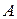 (0; –3; *) (0; –3; *) | 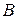 (1; 0; –2) (1; 0; –2) | 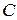 (–1; 0; *) (–1; 0; *) | 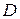 (0; 0; 1) (0; 0; 1) | 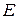 (–1; 1; *) (–1; 1; *) |
| 4.11 | 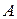 (1; 1; *) (1; 1; *) | 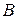 (1; 2; 3) (1; 2; 3) | 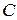 (0; 3; *) (0; 3; *) | 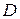 (–1;–2;–3) (–1;–2;–3) | 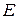 (2;–5; *) (2;–5; *) |
| 4.12 | 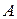 (2; 3; *) (2; 3; *) | 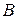 (1; –2; 1) (1; –2; 1) | 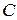 (–1; 0; *) (–1; 0; *) | 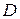 (1; –2; 0) (1; –2; 0) | 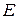 (–4; 0; *) (–4; 0; *) |
| 4.13 | 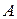 (3; –1; *) (3; –1; *) | 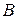 (0; 1; –1) (0; 1; –1) | 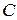 (–2; 3; *) (–2; 3; *) | 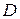 (0; –1; 0) (0; –1; 0) | 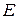 (1; –2; *) (1; –2; *) |
| 4.14 | 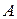 (4; 2; *) (4; 2; *) | 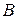 (1; 3; –1) (1; 3; –1) | 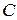 (–2; 1; *) (–2; 1; *) | 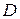 (3; 0; 1) (3; 0; 1) | 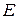 (0; –1; *) (0; –1; *) |
| 4.15 | 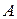 (5; –1; *) (5; –1; *) |  (3; 1; –2) (3; 1; –2) |  (0; 1; *) (0; 1; *) |  (2; 3; 0) (2; 3; 0) |  (1; 2; *) (1; 2; *) |
Продовження
