Определение коэффициентов сил трения качения методом наклонного маятника
Цель работы. Изучение явления трения качения и измерение коэффициентов трения качения различных материалов.
Приборы и принадлежности: установка наклонного маятника с закрепленными на ней пластинами из трех различных материалов; штангенциркуль.
Введение
Чтобы объяснить трение качения, необходимо учесть, что катящееся тело, например шар, и плоскость, по которой он движется, деформируются в области их соприкосновения, образуя зону контакта конечных размеров (C1C2 на рис. 63.1). Эта деформация несимметрична относительно катящегося тела, что и приводит к возникновению силы сопротивления – силы трения качения.
 Поясним количественно, как возникает эта сила и найдем ее величину. На рис. 63.1 рассмотрены силы, действующие на шар при его качении:
Поясним количественно, как возникает эта сила и найдем ее величину. На рис. 63.1 рассмотрены силы, действующие на шар при его качении:
F – сила, вызывающая движение шара;
Q – сила реакции опоры, Qn и Qt – ее нормальная и тангенциальная составляющие;
N – сила нормального давления.
Условия равновесия шара при его равномерном перемещении по плоскости записываются как обращение в ноль
а) суммы проекций сил на ось х:
F - Qt = 0, (1)
б) суммы проекций сил на ось у:
Qn - N = 0, (2)
в) суммы моментов сил относительно некоторой точки Св зоне контакта. Принимая плечо H силы F ввиду малости деформации равным радиусу шара r (то есть Н » r) и обозначая х-ю координату точки С через h, запишем:
Fr - Nh = 0. (3)
Как следует из формулы (3), с увеличением силы F увеличивается и h. Однако, ограниченность зоны контакта приводит к тому, что существует предельное значение силы F и, следовательно, предельное значение h, обозначаемое, как
hmах º k, (4)
при котором дальнейшее увеличение F приводит к нарушению равновесия. Это предельное значение силы F, равное согласно условию (1) предельному значению Qt, называют силой трения качения:
Qt = Fтр , (5)
а предельную величину “плеча” k момента нормальной составляющей силы реакции опоры Qn , равной согласно условию (2) силе нормального давления N,– коэффициентом трения качения. Коэффициент трения качения имеет размерность длины. Из уравнений (1), (3) – (5) следует выражение для силы трения качения, впервые полученное Кулоном:

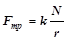 . (6)
. (6)
Метод измерения и описание аппаратуры
 В данной лабораторной работе для определения коэффициента трения качения используется метод наклонного маятника, предложенный А.С.Ах-матовым.
В данной лабораторной работе для определения коэффициента трения качения используется метод наклонного маятника, предложенный А.С.Ах-матовым.
Наклонный маятник представляет собой сочетание математического маятника с наклонной плоскостью (рис. 63.2). Установка для измерения коэффициента трения качения состоит из горизонтальной подставки, на которой находится наклонно расположенная линейка. К нижней части линейки перпендикулярно к ней прикреплены пластины из различных материалов. Над пластинами расположен угломер с горизонтальной шкалой для измерения углов отклонения нити маятника от положения равновесия. В верхней части линейки находится точка подвеса маятника, состоящего из металлического шара, подвешенного на нити. Если отвести маятник от положения равновесия и отпустить его, шар маятника начнет перекатываться (см. рис. 63.2) по пластине исследуемого материала, совершая затухающие колебания.
При малом затухании можно считать, что амплитуда колебаний маятника ji линейно убывает с увеличением номера колебания i, подчиняясь закону арифметической прогрессии. С целью упрощения расчетов, будем считать, что амплитуда колебаний изменяется скачком в начале каждого периода. Тогда путь S, пройденный шаром за n полных колебаний, по пластине исследуемого материала при начальном угле отклонения маятника от положения равновесия j0 и конечном угле отклонения от положения равновесия jn равен учетверенной сумме амплитуд колебаний ji от начальной амплитуды j0 до конечной jn:
S = 4 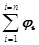 = 2n(j0 + jn) = 2nl(j0 + jn),
= 2n(j0 + jn) = 2nl(j0 + jn),
где l – длина нити маятника.
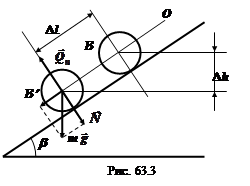
На рис. 63.3 показана наклонная плоскость и положение на ней шара при отклонении нити маятника на угол j0 (точка В на рис. 2) и при отклонении нити на угол jn (точка В' на рис. 2). Обозначим через DП разность потенциальных энергий маятника в поле сил тяжести в точках В и В'. Как следует из рис. 3,
DП = mgDh = mg Dl sinb, (8)
где DlиDh – разности положений центра шара вдоль наклонной плоскости и по вертикали соответственно;
b – угол наклона плоскости к горизонту (см. также рис. 63.2);
точка Вотвечает начальной амплитуде отклонения маятника j0;
точка B¢ – конечной амплитуде отклонения маятника jn.
Если маятник отпускается из положения первоначального отклонения без начальной скорости, а конечное отклонение соответствует крайнему положению, в котором кинетическая энергия равна нулю, то разность потенциальных энергий DП маятника в точках В и B¢ равна разности DЕ значений его полной энергии в тех же точках:
DЕ =DП. (9)
Изменение положения центра шара Dl за п полных колебаний, как следует из рис. 63.2, равно
Dl=l(cosjn-cosj0). (10)
Ввиду малости колебаний (начальные углы отклонения маятника j0£10°), можно считать, что сила трения качения не зависит от положения шара. Учитывая также, что N = mg cosb(см. рис. 63.3), запишем работу против сил трения качения на произвольном пути S:
Aтр = FтрS = k 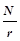 S =
S = 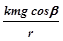 S. (11)
S. (11)
Убыль полной энергии маятника DE равна его работе против силы трения Атр. Из уравнений (7) – (11) находим коэффициент трения качения, выраженный через величины, измеряемые в эксперименте:
k = 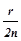 tgb
tgb 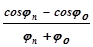 . (12)
. (12)
Заметим, что при выводе формулы (12) не учитывались: работа по преодолению сил сопротивления воздуха, работа сил трения в подвесе, изменение потенциальной энергии волокон нити при ее закручивании в двух крайних положениях маятника; не рассматривалось влияние на измерение коэффициента трения качения таких факторов, как проскальзывание шара, упругий гистерезис соприкасающихся тел и их адгезия. Студентам, желающим познакомиться с этими вопросами, рекомендуем обратиться к специальной литературе [1, 2].
Порядок выполнения работы
1. С помощью опорного винта линейки установите плоскость колебаний маятника под некоторым углом b (его следует выбирать в интервале от30°до60°). Измерьте этот угол с помощью транспортира, расположенного на подставке позади линейки (при измерениях учтите, что b = 90°- g, где g - угол, значение которого определяется с помощью транспортира на установке). Значение угла b занесите в первый столбец таблицы 1.
Таблица 1
| МАТЕРИАЛ 1 | ||||
| b | № пп. | jm | jср1 | k1 |
| … | ||||
| … | ||||
| … | ||||
| kср1 = |
Таблица 2
| МАТЕРИАЛ 2 | ||||
| b | № пп. | jm | jср2 | k2 |
| … | ||||
| … | ||||
| … | ||||
| kср2 = |
Таблица 3
| МАТЕРИАЛ 3 | ||||
| b | № пп. | jm | jср3 | k3 |
| … | ||||
| … | ||||
| … | ||||
| kср3 = |
2. Приведите в соприкосновение поверхность шара с первым из трёх исследуемых образцов.
3. При помощи опорных винтов в подставке установите ее в такое положение, при котором нить маятника окажется против нулевого деления шкалы угломера.
4. Отклоните маятник от положения равновесия на угол j0»5° и без начальной скорости отпустите маятник. Измерьте амплитудное значение угла jm после 10 полных колебаний. Проделайте опыт 6 раз, измеряя значения конечных углов отклонения j1, j2, … j6 при одном и том же в каждом опыте начальном угле j0. Значения конечных углов отклонения запишите в клетки третьего столбца таблицы 1. По полученным данным вычислите jср1:
jср1 = 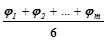 . (13)
. (13)
Полученное значение jср1 занесите в четвёртый столбец таблицы 1.
5. Повторите измерения по пп. 2 ¸ 4 для второго исследуемого образца. Значения конечных углов отклонения запишите в клетки третьего столбца таблицы 2. По полученным данным и формуле (13) вычислите jср2.
6. Повторите измерения по пп. 2 ¸ 4 для образца номер 3, значения конечных углов отклонения запишите в клетки третьего столбца таблицы 3.
7. Измените угол b наклона плоскости колебаний маятника. Повторите измерения и вычисления, описанные в пп. 2 ¸ 6, для нового значении этого угла. Данные измерений для каждого из трёх исследуемых материалов занесите в соответствующие таблицы.
8. Еще раз измените угол наклона b. Вновь повторите измерения по пп. 2 ¸ 4 для каждого из трёх материалов. Данные измерений занесите в соответствующие таблицы.
9. С помощью штангенциркуля измерьте диаметр шара и вычислите его радиус r. Запишите полученные значения.
10. Используя три значения jср1для каждого из углов наклона b, по формуле (12) вычислите три значения коэффициента трения k1 для первого материала, а затем – его среднеарифметическое значение kср1. Результаты вычислений занесите в таблицу 1.
ВНИМАНИЕ: прежде чем использовать формулу (12), углы j и j0 следует перевести в радианы:j(рад)=j(град)´ p¤180.
Повторите вычисления для второго материала. Результаты вычислений коэффициента трения k2 и его среднеарифметического значения kср2 занесите в таблицу 2.
Повторите вычисления для материала 3. Результаты вычислений коэффициента трения k3 и его среднеарифметического значения kср3 занесите в таблицу 3.
11. Для каждого из трёх материалов рассчитайте свою максимальную относительную приборную ошибку косвенного измерения коэффициента трения качения D1k/kср по формуле
|
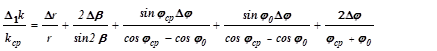
В эту формулу подставьте значение r, найденное в п. 9, и значения b, j0, 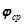 , занесенные в таблицу. Значение угла b возьмите минимальным из тех, которые устанавливались в ходе измерений на данном материале. В вычислениях следует принять, что Dr = 0,1мм, Db =2°,Dj =0,5°.
, занесенные в таблицу. Значение угла b возьмите минимальным из тех, которые устанавливались в ходе измерений на данном материале. В вычислениях следует принять, что Dr = 0,1мм, Db =2°,Dj =0,5°.
12. Для каждого из трёх материалов рассчитайте свою относительную случайную ошибку косвенного измерения коэффициента трения качения D2k/kср по формуле:
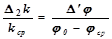 . (15)
. (15)
Выражение (15) получается так: если вспомнить, что для малых углов, выраженных в радианной мере, cos j » 1 - 0,5j2, то из (12) следует:
k = 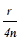 tgb (j0 - jcp).
tgb (j0 - jcp).
Очевидно, что при неизменных r, n,j0, b
½Dk½= 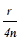 tgb ½Dj½.
tgb ½Dj½.
Разделив два последних уравнения одно на другое, получим формулу (15).
Доверительный интервал D¢j в формуле (15) рассчитывается по значениям j1, j2, … j6, измеренным при минимальном значении угла b (для данного материала). Для этого примите значение доверительной вероятности W = 95% и, учитывая, что при такой доверительной вероятности для числа измерений т= 6 значение коэффициента Стьюдента aCт равно 2,6, вычислите значение D¢j:
D¢j = aСт 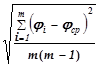 . (16)
. (16)
|
, (17)
где коэффициенты kсри Dk измеряются в метрах.
Контрольные вопросы
1. Почему невозможно объяснить происхождение силы трения качения исходя из представления об абсолютно твердом теле?
2. Какова относительная скорость точек касания поверхностей тел: а) в случае трения скольжения; б) в случае трения качения?
3. При каком условии начинается качение шара по плоскости?
4. Почему сила реакции плоскости в общем случае не совпадает с направлением нормали к ней?
5. Почему сила реакции опоры несколько смещена вперед по направлению движения шара?
6. От каких факторов зависит величина силы трения качения?
7. Почему можно считать, что амплитуда колебаний наклонного маятника убывает по закону арифметической прогрессии?
8. Выведите формулу (12).
9. Получите формулу (16).
10. Укажите источники систематических ошибок измерения коэффициента трения качения в данной работе.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Ахматов А. С. Молекулярная физика граничного трения.- М.: Наука, 1963. - Т. II, гл. 9, 11.
2. Кильчевский И.А. Курс теоретической механики.- М.: Наука. 1972. - Т. 1.
3. Методические указания к лабораторным работам по физике. Механика. Работы 60 - 63. - М.: Изд. МИИТа, 1976. - Раздел «Ошибки измерения физических величин. Вычисление ошибок косвенных измерений».
4. Расчет погрешностей в лабораторных работах физического практикума. Методические указания к вводным занятиям в физическом практикуме/ Н.А.Гринчар, Ф.П.Денисов, Б.А.Курбатов и др.; Под общ. ред. Ф.П.Денисова. - М.: МИИТ, 1995. - 38 с.
С О Д Е Р Ж А Н И Е
| Работа 6 | Определение момента инерции махового колеса методом колебаний. . . . . . . . . . . . . . . . . . . . . . . . . . . | . . 3 |
| Работа 61 | Определение моментов инерции тел методом крутильных колебаний . . . . . . . . . . . . . . . . . . . . . . . . . . | . .12 |
| Работа 63 | Определение коэффициентов сил трения качения методом наклонного маятника. . . . . . . . . . . . . . . . . . . . . | . .20 |
Учебно-методическое издание
Надежда Александровна Государева,
Сергей Михайлович Кокин
