Измерениями с однократными наблюдениями

Число наблюдений при практическом проведении измерений всегда ограничено, и чем сложнее эксперимент и выше его стоимость, тем оно меньше. В практике электрорадиоизмерений зачастую приходится ограничиваться измерениями с однократными наблюдениями (однократными измерениями).

В случае измерений с многократными наблюдениями необходима статистическая обработка результатов наблюдений. Для однократных измерений она не нужна, что значительно упрощает оценку погрешностей. Более того, при однократных измерениях должна быть соблюдена процедура, обеспечивающая получение результата измерения с погрешностью, не превышающей допускаемую. Ожидаемую погрешность результата измерения оценивают перед измерением (априорная оценка), используя предварительные данные об измеряемой величине, применяемых методе измерений и средствах измерений, а также об условиях проведения измерений.

Для априорной оценки ожидаемой погрешности результата однократного измерения рекомендуется следующий алгоритм.

1. Проводится анализ составляющих погрешности результата измерения по источникам возникновения. Методические погрешности оцениваются либо на основании изучения теоретических зависимостей, описывающих исследуемый объект и метод измерений, либо экспериментальным путем при измерении одной и той же величины различными методами. Для оценки инструментальных и внешних погрешностей используются данные об основных и дополнительных погрешностях применяемых средств измерений. Наконец, субъективные погрешности оцениваются, как правило, экспериментальным путем. При этом оценка систематических погрешностей дается их границами (пределами), а случайных - значениями средних квадратических отклонений (с.к.о.).

2. Неисключенные систематические погрешности суммируются для определения Δ_S . Суммирование выполняется с помощью формул, приведенных в методических указаниях к лабораторной работе 1.2

3. Оценивается с.к.о. результата измерения в предположении, что все выявленные отдельные случайные погрешности, имеющие оценки с.к.о: 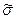_j (j = l,..,k), независимы. Поэтому для оценки с.к.о. результата измерения 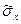используется формула:

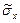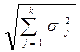= (2.1)

4. С помощью коэффициента Стьюдента находят доверительную границу случайной погрешности 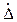по формуле:

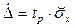(2.2)

Для однократных измерений приняты следующие значения t_p : при Р = 0,95 t_p= 2, а при Р = 0,95 t_p= 2,6.

5. Производится оценка доверительной границы ожидаемой погрешности результата измерения. Для прямых однократных измерений рекомендуется вычислять отношение 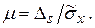(по аналогии с многократными наблюдениями). Если μ < 0.5, можно принять ,

Δ = 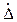, а при μ > 8 , Δ = Δ_S . Внутри этого интервала значение Δ можно найти по формуле:

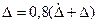(2.3)

где коэффициент 0.8 учитывает малую вероятность того, что Δ_s и 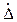одновременно будут иметь свои граничные значения. В случае косвенных измерений правильнее пользоваться формулой:

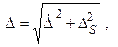(2.4)

Таким образом, можно записать:

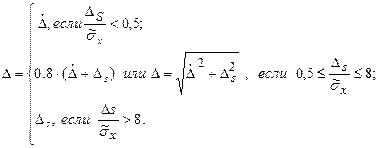(2.5)

Если полученное значение Δ оказалось больше допускаемой погрешности Δ_∂ необходимо, либо обратиться к другому методу измерений, либо заменить средства измерений, либо, наконец, изменить определенным образом условия проведения измерений. Если же Δ ≤ Δ_∂, установленная процедура измерений должна обеспечить получение результата измерения с требуемой точностью.

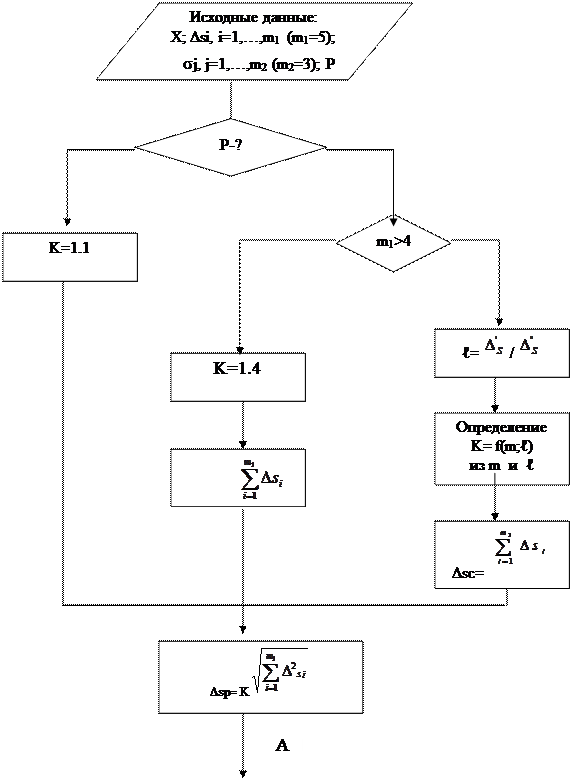
Алгоритмы оценки погрешностей для случаев однократных прямых

и косвенных измерений приведены на рисунках 2.1 и 2.2 .

P=0.95 P=0.99

Да Нет

Рис. 2.1 Алгоритм оценки погрешности при однократном прямом

измерении

Р=0.95 А

P=0.99

Да Нет

P=0.95 P=0.99

m<0.5 m>8

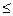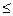0.5 m 8

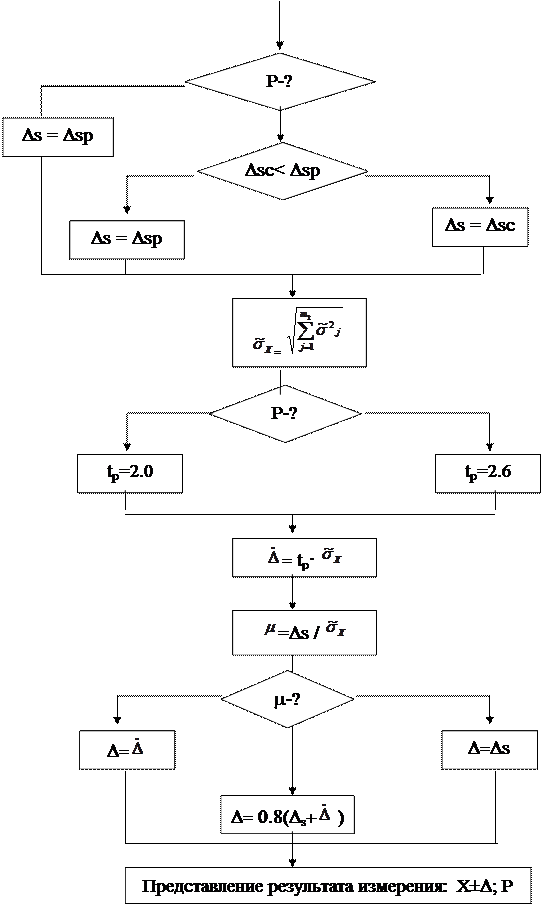
Продолжение рисунка 2.1

P=0.95 P=0.99

А

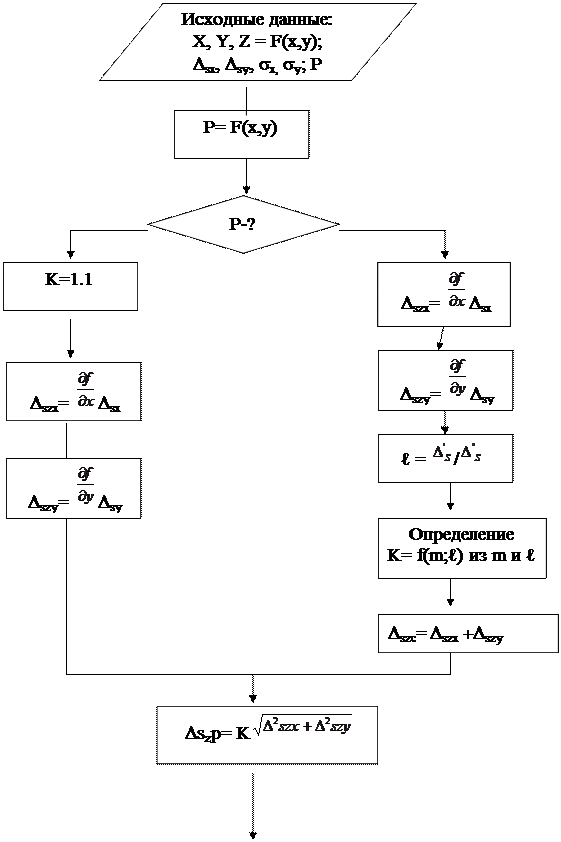
Рис. 2.2 Алгоритм оценки погрешности при однократном косвенном

измерении

А

P=0.95 P=0.99

Да Нет

P=0.95 P=0.99

m<0.5 m>8

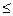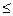0.5 m 8

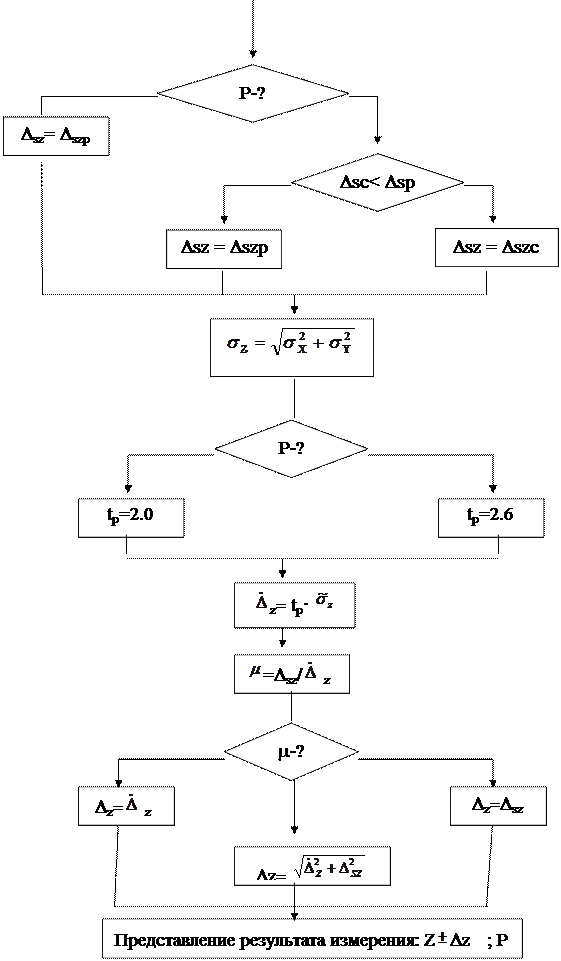
Продолжение рисунка 2.2