Энергия системы зарядов, уединенного проводника и конденсатора. Энергия электростатического поля

1. Энергия системы неподвижных точечных зарядов.

Потенциальная энергия системы двух неподвижных точечных зарядов Q₁ и Q₂, находящихся на расстоянии r друг от друга:

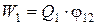и

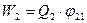
где j₁₂ и j₂₁ – соответственно потенциалы, создаваемые зарядом Q₂в точке нахождения заряда Q₁ и зарядом Q₁, в точке нахождения заряда Q₂.

Потенциал поля, создаваемый точечным зарядом:

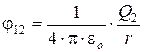и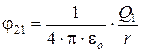

поэтому

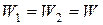
и

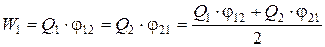
Добавляя к системе из двух зарядов последовательно заряды Q₃, Q₄, …, в случае n зарядов:

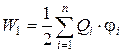(12.1)

где j_i – потенциал, создаваемый в той точке, где находится заряд Q_i,всеми зарядами, кроме i-го.

Энергия заряженного уединенного проводника.

Пусть имеется уединенный проводник, заряд, ёмкость и потенциал которого соответственно равны Q, С, j. Увеличим заряд этого проводника на dQ. Для этого необходимо перенести заряд dQ из бесконечности на уединённый проводник, затратив на это работу, равную

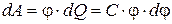
Чтобы зарядить тело от нулевого потенциала до j, необходимо совершить работу

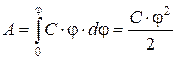(12.2)

Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник:

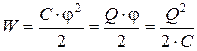(12.3)

Принимая потенциал проводника равным j, энергия проводника

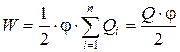
где 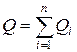– заряд проводника.

Энергия заряженного конденсатора.

Как всякий заряженный проводник, конденсатор обладает энергией, которая в соответствии с формулой (12.3) равна

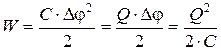(12.4)

где Q – заряд конденсатора, С – его ёмкость, Dj – разность потенциалов между обкладками.

Используя выражение (12.4), можно найти механическую (пондеромоторную) силу,с которой пластины конденсатора притягивают друг друга.

Действующая сила совершает работу

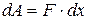
вследствие уменьшения потенциальной энергии системы

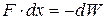
откуда

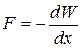(12.5)

Подставив в (12.4) выражение (11.3), по­лучим

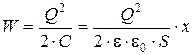(12.6)

Производя дифференцирование при конкретном значении энергии, найдем искомую силу:

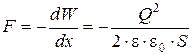
где знак минус указывает, что сила F является силой притяжения.

Энергия электростатического поля.

Преобразуем формулу (12.4), выражающую энергию плоского конденсатора посредством зарядов и потенциалов, воспользовавшись выражением для ёмкости плоского конденсатора

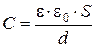
и разности потенциалов между его обкладками ( ).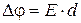

Тогда получим

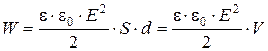(12.7)

где V=Sd – объем конденсатора.

Формула (12.7) показывает, что энергия конденсатора выражается через величину, характеризующую электростатическое поле, - напряженность Е.

Объемная плотностьэнергии электростатического поля (энергия единицы объема)

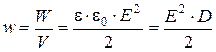(12.8)

Выражение (12.8) справедливо только для изотропного диэлектрика,для которого выполняется соотношение:

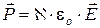
ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК