Некоторые виды иррациональных уравнений

1).Уравнения вида 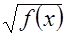= 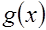. (3)

Так как в ОДЗ левая часть уравнения всегда неотрицательна, то уравнение может иметь решение только тогда, когда 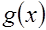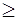0. В этом случае обе части данного уравнения неотрицательны, и их возведение в квадрат даёт равносильное в ОДЗ уравнение. Таким образом, получаем:

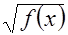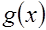
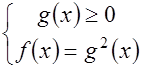= . (4)

В этом равносильном переходе требование 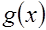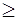0 задаёт ОДЗ. Однако если искать ОДЗ довольно сложно, то проще подставить найденные корни уравнения 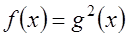либо в исходное уравнение, либо проверить истинность неравенства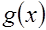 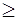0 при подстановке в него этих корней.

Замечание. Нет необходимости проверять условие 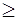0, поскольку оно автоматически выполняется при решении уравнения системы (4).

Пример 3. Решить уравнение .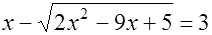

Δ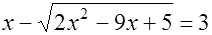

.

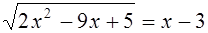
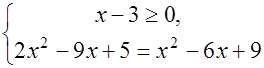
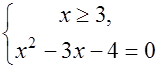
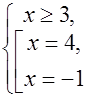
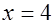Ответ: .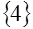

Замечание. Это уравнение можно решить другим способом, не применяя последовательных равносильных преобразований. После возведения в квадрат обеих частей уравнения 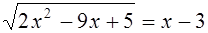получим уравнение-следствие: 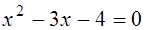. Его корни 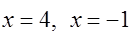. Для выявления возможных посторонних корней необходимо сделать проверку. Подставляя поочерёдно в данное уравнение найденные значения ,получаем:

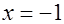- не является корнем, 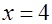- корень уравнения.

2).Уравнения вида 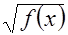= 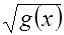(5)

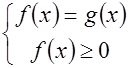
или (5) .

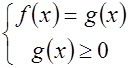При таком способе решения достаточно проверить неотрицательность одного из подкоренных выражений.

Пример 4. Найдите произведение корней уравнения .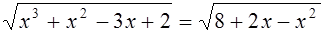

Δ Воспользуемся вторым условием равносильности:

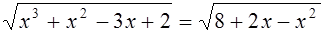
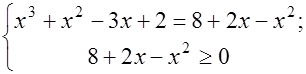
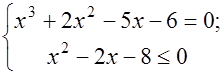
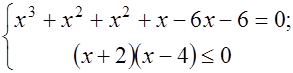
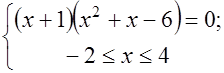
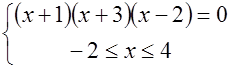
Значит произведение корней равно .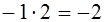

Ответ: .

3).Уравнения, сводящиеся к рациональным при помощи замены переменной

Как правило, способ подстановки удобен, когда в уравнение входят радикалы разных степеней.

Пример 5. Решить уравнение + .

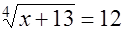Δ Обозначим 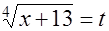, где t 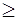0, тогда 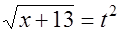и данное уравнение запишется в виде .

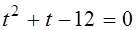По теореме Виета его корни .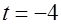

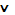
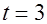Так как найденные значения 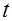должны удовлетворять неравенству t 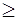0, то данное уравнение равносильно .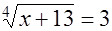

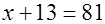
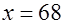Ответ: .

Пример 6. Решить уравнение .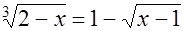

Δ Обозначим 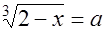, , 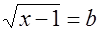где 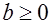. Заметим, что , , 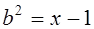тогда .

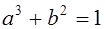Для нахождения 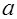и 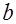нужно решить систему:

.

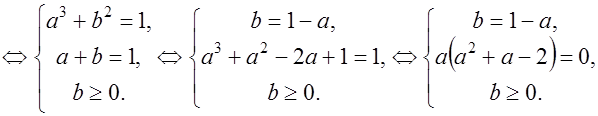
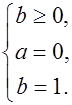
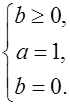Воспользовавшись обратной заменой, получим:

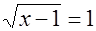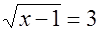или или .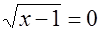

Следовательно, , , .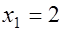

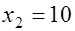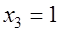Проверкой убеждаемся, что найденные значения 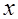являются корнями исходного уравнения.

Ответ: .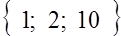

Замечание. Существует достаточно много способов решения иррациональных уравнений. Рассмотрим, например, комбинированный способ решения, когда метод подбора корней сочетается с графическим способом.

Пример 7. Решить уравнение .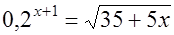

Δ Преобразуем данное уравнение.

.

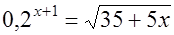
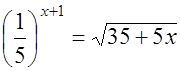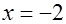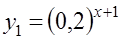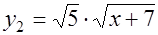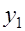
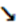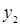
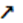Легко увидеть, что - корень данного уравнения. Осталось показать, что других корней уравнение не имеет. Для этого рассмотрим графики функций и . Обе функции непрерывны и строго монотонны на общей области определения, причём , а на 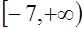. Поэтому графики этих функций не могут иметь более одной общей точки. Следовательно, 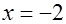- единственный корень данного уравнения. Ответ: .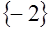