Определение декремента затухания , силы сопротивления вязкой среды, и добротности колебательной системы при колебаниях подвешенного на пружине тела в вязкой среде

Лабораторная работа № 128

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ МЕХАНИЧЕСКИХ КОЛЕБАНИЙ

ПРУЖИННОГО МАЯТНИКА

Цель работы:

Определение декремента затухания , силы сопротивления вязкой среды, и добротности колебательной системы при колебаниях подвешенного на пружине тела в вязкой среде.

Метод измерения и расчётные соотношения.

Пружинным маятником называется система, состоящая из упругой пружины и груза подвешенного на ней. В общем случае движение пружинного маятника в поле силы тяжести довольно сложно и описывается большим числом степеней свободы. Практический интерес, однако, представляют колебания с одной степенью свободы, когда движение маятника происходит вдоль вертикальной оси.

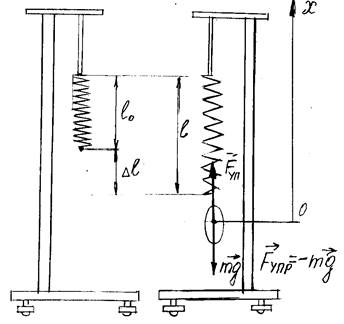Рис.1

Для полного описания колебаний в этом случае необходимо знать поведение только одной переменной, например, вертикальной координаты центра масс тела маятника. Теоретически пружинный маятник может совершать незатухающие механические колебания при условии, что пружина является идеально упругой, а тело движется в окружающей среде без трения. На тело, подвешенное на пружине в поле силы тяжести, действуют две силы (без учета сил трения) сила тяжести 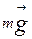и упругая сила 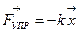. Начало координат выберем в центре тяжести тела. При этом сила тяжести будет скомпенсирована некоторым начальным растяжением пружины Δl в дальнейшем рассмотрении участвовать не будет.

При отклонении тела от точки равновесия будет возникать возвращающая сила F(х). Рассмотрим колебания пружинного маятника с малой амплитудой. Для пружинного маятника условия малости колебаний удовлетворяются при смещениях, Уравнение движения пружинного маятника при этом имеет вид

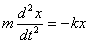(1)

где: k - коэффициент жесткости пружины, m - масса маятника.

Если физическая величина x(t) изменяется со временем по гармоническому закону

(2)

то колебания называются гармоническими. В функции (2) А — амплитуда колебаний;w - круговая частота

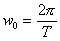T — период колебаний; t — время , пошедшее от начала колебаний; φ₀—начальная фаза колебаний. Функция х{t) из (1) представляет решение дифференциального уравнения

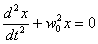(3)

называемого уравнением свободных колебаний. Физическую систему, выведенную из состояния равновесия и представленную самой себе, в которой изменение одного из параметров х описывается дифференциалльным уравнением (3) называют классическим гармоническим осциллятором. Сравнивая (2) с (2), получим

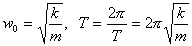(4)

В реальных осцилляторах, за счет сил сопротивления ( в большей степени трения), происходит рассеяние (диссипация) запасенной энергии, в результате чего свободные колебания со временем затухают. Если жидкость неподвижна, а скорость движения тела невелика, то перемещение тела не оказывает влияния на удалённые слои жидкости. Взаимодействие происходит только со слоем, непосредственно соприкасающимся с телом. При движения пружинного маятника в вязкой среде, с небольшими скоростями сила сопротивления пропорциональна скорости движения

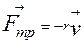(5)

где коэффициент r зависит от вязкости среды и площади соприкосновения поверхности S

тела с жидкостью

r ~ηS

(6)

где η – коэффициент внутреннего трения жидкости ( динамическая вязкость жидкости)

Дж. Стокс эмпирически установил, что для тел сферической формы радиуса R коэффициент сопротивления равен 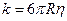. Следовательно, сила сопротивления среды равна

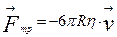(7)

При равномерном движении сферы в идеальной (не вязкой) жидкости, она не испытывает никакого сопротивления. Выводы Стокса для сферы верны также для эллипсоида вращения и других тел с подобными поверхностями.

Сила Архимеда, действующая, на груз и направленная в одну и ту же сторону, будет скомпенсирована некоторым начальным растяжением пружины Δl в дальнейшем рассмотрении участвовать не будет.

Для описания движения груза пружинного маятника в вязкой среде необходимо в правую часть уравнения (1) величину силы трения (5). Поэтому свободные колебания будут затухающими (следовательно, не гармоническими). В результате второй закон динамики для механического осциллятора при наличии вязкого трения можно записать так:

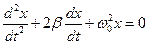(8)

где 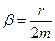- коэффициент затухания; 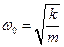- собственная частота незатухающих колебаний.

Можно показать, что решением этого уравнения является функция

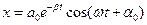(9)

где 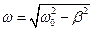- частота затухающих колебаний .

Отношение двух соседних амплитуд 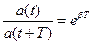называется декрементом затухания.

Величина 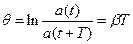- называется логарифмическим декрементом затухания.

По истечение N колебаний эта величина определяется по формуле

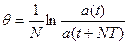(10)

Энергия пружинного маятника пропорциональна квадрату амплитуды колебаний

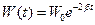(11)

где 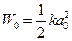- энергия пружины при максимальной начальной амплитуде, то есть начальный запас энергии пружинного маятника.

Потеря энергии маятника за период равна

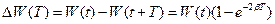(12)

Из (10) и (11) следует

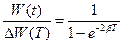(13)

При малых затуханиях 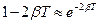и соотношение (12) можно преобразовать к виду

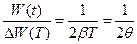(14)

Описание схемы установки.

На Рис. 2 представлена схема установки. На платформе 1 расположены стойка 3, к которой подвешена пружина 8, стеклянный цилиндр с жидкостью 4, секундомер 2 для отсчёта числа колебаний за установленные интервалы времени, инфракрасный датчик 9 для отсчёта числа колебаний флажка 7, закреплённого на штоке 6. На штоках 6 крепятся грузы - металлический шар или эллипсоид. Консоль 11 держит подвесную систему.

Для проведения опытов необходимы следующие средства измерений:

1 .Электронный секундомер с точностью отсчёта ± 0,01с , для измерения времени и установленного числа колебаний груза. В установке используется программируемый электронный секундомер, измеряющий число прохождений флажка 7 через луч датчика 9 за установленное время (10 секунд).

2. Линейка с миллиметровой шкалой 10, закреплённая на стойке 3, для измерений смещений груза по вертикали.

Выполнение работы.

1. Вращением ножек основания установить стойку 3 в вертикальное положение.

2. Измерить с помощью линейки длину пружины без груза .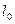

3. Установить консоль 11 так чтобы подвесная система находилась вне цилиндра 4, закрепить на конце пружины шток 6 с выбранным грузом (металлические шар или эллипсоид известной массы) и измерить длину пружины с грузом 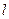, отсчитав положения её первого и последнего витка по миллиметровой шкале.

4. Установить консоль 11 так, чтобы подвесная система находилась внутри цилиндра 4.

5. Включить секундомер 2.

6.С помощью штока 6 переместить груз вертикально вниз до момента пересечения флажком 7 луча датчика 11. При этом измеритель числа колебаний должен показать О. Произвести отсчёт на миллиметровой шкале 12 положения флажка 7 ( начальное отклонение груза 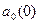от положения равновесия).

7. Отпустить шток 6 и привести в движение маятник.

8. По истечении установленного времени (10 секунд отсчитываются прибором автоматически и не показываются на табло счётчика) записать показания электронного счётчика, который измерит число Z прохождений флажка через луч датчика 9 за десять секунд.

9. Нажать кнопку 13 электронного счётчика. При этом он покажет общее число прохождений флажка 7 через луч датчика 9 от начала процесса колебаний.

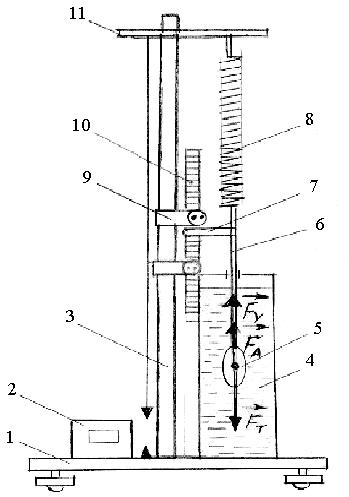Рис. 2

10.Произвести отсчёт амплитуды выбранного последнего колебания 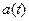флажком 7 на шкале

11. Для статистической обработки измеренных величин пункты 6 и 10 повторить не менее 5 раз.

12. Повторить для двух грузов – шара и эллипсоида.