Определение контанты диссоциации слабого электролита и проерка закона разведения оствальда

по дисциплине Физическая химия

наименование учебной дисциплины

Выполнил

Студент, группы НМб-12-1 (подпись) А.В.Тищенко

(дата)

27.12.13

Принял

Преподаватель (подпись) Ф.М.Лебедь

(дата)

Иркутск –2013

1 Краткое теоретическое введение

В растворе электролита ток переносится катионами и анионами.

Т.к. с увеличением разведения величины степени диссоциации α и коэффициента электрической проводимости 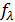cтремящееся к единице, то эквивалентная электрическая проводимость при этом стремится к наибольшему значению :

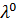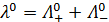(1)

где 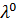- эквивалентная электрическая проводимость электролита при бесконечном разведении; 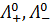- предельные подвижности ионов.

Уравнение (1) называется законом Кольрауша, который устанавил, что в сильных электролитах можно наблюдать, например, следующую закономерность:

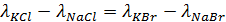и т.п.

Т.е. физическая сущность этого закона состоит в том, что в разбавленных растворах электролитов катионы и анионы переносят электрический ток независимо друг от друга.

В растворах слабых электролитов, если концентрация ионов мала, межионные взаимодействия выражены гораздо меньше и можно считать 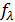равное единице, тогда отношение эквивалентной электрической проводимости для раствора конечной концентрации к электрической проводимости при бесконечном разведении равно степени диссоциации, т.е.

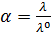(2)

2 Расчетная часть

Примечание – В начале опыта измеряют удельную электрическую проводимость воды (ᴂ_H2O), которая равна 10*10^-4

2.1 Раствор муравьиной кислоты

Изначально рассчитывается эквивалентная электрическая проводимость:

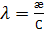(3)

где 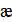– удельная электрическая проводимость [См/м];

С – концентрация [моль/м³];

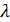– эквивалентная электрическая проводимость .

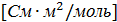Далее измеренные единицы будут переведены в единицы системы СИ

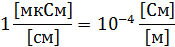
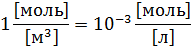
После чего по формуле (3) произвожу расчет для разных концентраций:

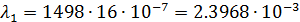
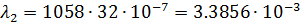
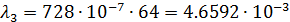
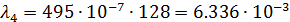
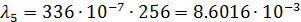
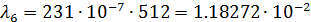
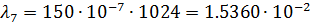
Рассчитаем степень диссоциации по формуле:

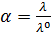(4)

где 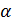– степень диссоциации;

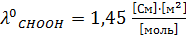(взято из табл.).

Рассчитываем по формуле (4) :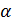

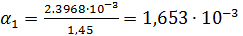
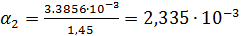
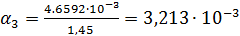
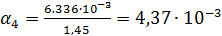
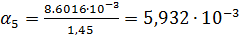
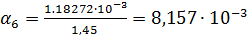
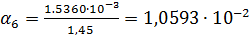
Константа диссоциации рассчитывается по формуле:

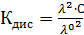(5)

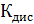[моль/См*м²

По формуле (5) рассчитываем :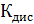

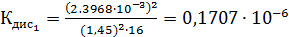
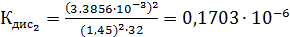
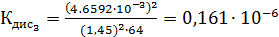
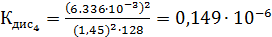
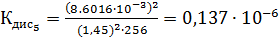
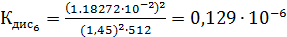
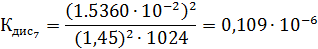
Среднее из всех вышеперечисленных значений будет равно 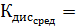0,1469 .

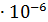Таблица 1 – результаты измерений для муравьиной кислоты

С (моль/литр)	ᴂ, ( 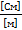)	λ, ( )		( )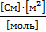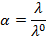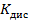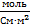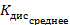
1/16	1498·10-4	0,002397	0,001653		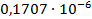0,1469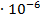
1/32	1058·10-4	0,003386	0,002335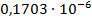
1/64	728·10-4	0,004659	0,003213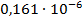
1/128	495·10-4	0,006336	0,00437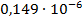
1/256	336·10-4	0,008602	0,005932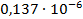
1/512	231·10-4	0,011827	0,008157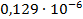
1/1024	150·10-4	0,01536	0,010593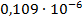

2.2 Раствор уксусной кислоты

Аналогично предыдущему разделу, по формуле (3) рассчитывается эквивалентная электрическая проводимость. Затем рассчитывается степень диссоциации по формуле (4). Далее - константа диссоциации по формуле (5). Ввиду того, что выше пошагово был описан ход работы, конечные результаты приведены в таблице 2

Таблица 2 – результаты измерений для уксусной кислоты

С (моль/литр)	ᴂ, ( 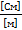)	λ, ( )		( )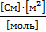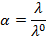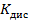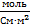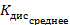
1/16	1028·10-4	0,001645	0,001134		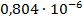0,936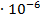
1/32	783·10-4	0,002506	0,001728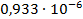
1/64	546,5·10-4	0,003498	0,002412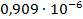
1/128	400·10-4	0,00512	0,003531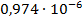
1/256	278·10-4	0,007117	0,004908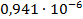
1/512	202,65·10-4	0,010376	0,007156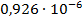
1/1024	142,8·10-4	0,014623	0,010085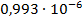

3 Графическая часть

3.1 Муравьиная кислота

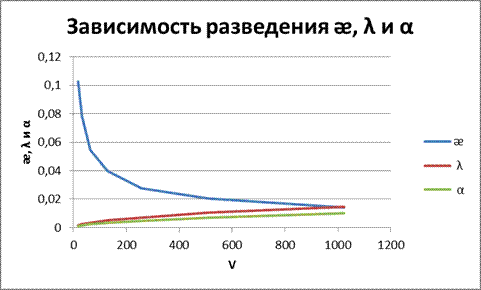
Рисунок 1 – Зависимость от разведения ᴂ, λ и α

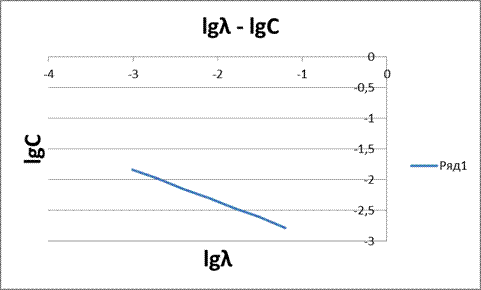
Рисунок 2 - Зависимость lgλ – lgC

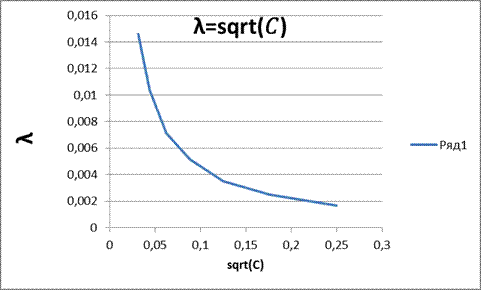
Рисунок 3 – Зависимость λ=sqrt(𝐶)

3.2 Уксусная кислота

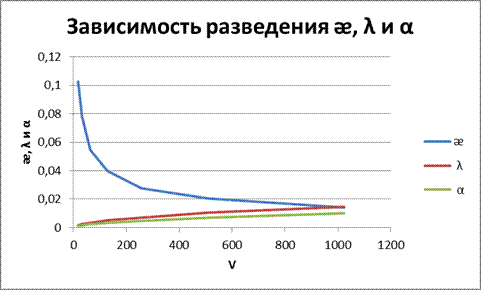
Рисунок 4 – Зависимость от разведения ᴂ, λ и α

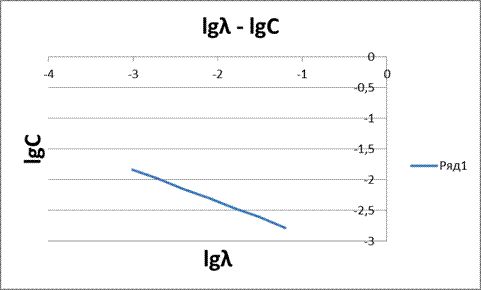
Рисунок 5 - Зависимость lgλ – lgC

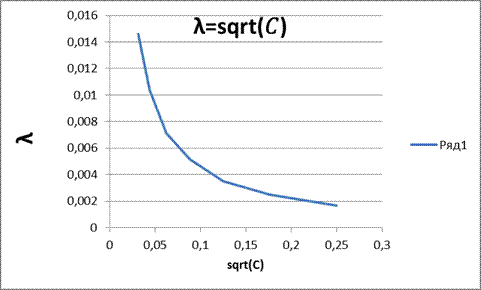
Рисунок 6 – Зависимость λ=sqrt(𝐶)

Вывод

В ходе эксперимента была исследована зависимость удельной, эквивалентной, электрической проводимостей растворов слабого электролита. Было построено несколько графиков, демонстрирующих результаты проведенного опыта. Кроме того, была рассчитана константа диссоциации слабого электролита.