| | | Вычислить площадь треугольника, вершинами которого являются точки: |
| | 116.1 | A(2; -3), B(3; 2), C(-2; 5); |
| | 116.2 | M1(-3; 2), M2(5; -2), M3(1; 3); |
| | 116.3 | M(-3; 4), N(-2; 3), P(4; 5).  |
| | | Вершины треугольника суть точки A(3; 6), B(-1; 3), C(2; -1). Вычислить длину его высоты, проведенной из вершины С.  |
| | | Определить площадь паралелограмма три вершины которого суть точки A(-2; 3), B(4; -5), C(-3; 1).  |
| | | Три вершины параллелограмма суть точки A(3; 7), B(2; -3), C(-1; 4). Вычислить длину его высоты, опущенного из вершины В на сторону АС  |
| | | Даны последовательные вершины однородной четырехугольной пластинки A(2; 1), B(5; 3), C(-1; 7), D(-7; 5). Определить координаты ее центра масс.  |
| | | Даны последовательные вершины A(2; 3), B(0; 6), C(-1; 5), D(0; 1), E(1; 1) однородной пятиугольной пластинки. Определить координаты ее центра масс.  |
| | | Площадь треугольника S=3, две его вершины суть точки A(3; 1), B(1; -3), а третья вершина С лежит на оси Oy. Определить координаты вершины С.  |
| | | Площадь треугольника S=4, вде его вершины суть точки А(2; 1), B(3; -2), а третья вершина С лежит на оси Ox. Определить координаты вершины С.  |
| | | Площадь треугольника S=3, две его вершины суть точки A(3; 1), B(1; -3), центр масс этого треугольника лежит на оси Ox. Определить координаты третьей вершины С.  |
| | | Площадь параллелограмма S=12; две его вершины суть точки A(-1; 3), B(-2; 4). Найти две другие вершины этого параллелограмма при условии, что точка пересечения его диагоналей лежит на оси абсцисс.  |
| | | Площадь параллелограмма S=17; две его вершины суть точки A(2; 1), B(5; -3). Найти две другие вершины этого параллелограмма при условии, что точка пересечения его диагоналей лежит на оси ординат.  Глава 7. Преобразование координат Глава 7. Преобразование координат | | | Написать формулы преобразований координат, если начало координат (без изменения направления осей) перенесено в точку: | | | 127.1 | А(3; 4); | | | 127.2 | B(-2; 1); | | | 127.3 | C(-3; 5).  | | | | Начало координат перенесено (без изменения направления осей) в точку O’(3; -4). Координаты точек А(1; 3), B(-3; 0), C(-1; 4) определены в новой системе. Вычислить координаты этих же точек в старой системе координат.  | | | | Даны точки A(2; 1), B(-1; 3), C(-2; 5). Найти их координаты в новой системе, если начало координат перенесено (без изменения направления осей): | | | 129.1 | в точку А; | | | 129.2 | в точку В; | | | 129.3 | в точку С.  | | | | Определить старые координаты начала O’ новой системы, если формулы преобразования заданы следующими равенствами: | | | 130.1 |  , ,  ; ; | | | 130.2 |  , ,  ; ; | | | 130.3 |  , ,  ; ; | | | 130.4 |  , ,  ; ;  | | | | Написать формулы преобразований координат, если координатные оси повернуты на один из следующих углов: | | | 131.1 | 600; | | | 131.2 | –450; | | | 131.3 | 900; | | | 131.4 | –900; | | | 131.5 | 1800.  | | | | Координатные оси повернуты на угол  =600. Координаты точек А( =600. Координаты точек А( 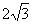 ; -4), B( ; -4), B( 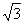 ; 0), C(0; ; 0), C(0; 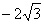 ) определены в новой системе. Вычислить координаты этих же точек в старой системе. ) определены в новой системе. Вычислить координаты этих же точек в старой системе.  | | | | Даны точки M(3; 1), N(-1; 5), P(-3; -1). Найти их координаты в новой системе, если оси координат повернуты на угол: | | | 133.1 | –450; | | | 133.2 | 900; | | | 133.3 | –900; | | | 133.4 | 1800.  | | | | Определить угол  , на который повернуты оси, если формулы преобразования координат заданы следующими равенствами: , на который повернуты оси, если формулы преобразования координат заданы следующими равенствами: | | | 134.1 |  , ,  ; ; | | | 134.2 |  , ,  ; ;  | | | | Определить координаты точки O’ – нового начала координат, если точка А(3; -4) лежит на новой оси абсцисс, а точка B(2; 3) лежит на новой оси ординат, причем оси старой и новой систем координат имеют соответственно одинаковые направления.  | | | | Написать формулы преобразования координат, если точка M1(2; -3) лежит на новой оси абсцисс, а точка M2(1; -7) лежит на новой оси ординат, причем оси старой и новой систем координат имеют соответственно одинаковые направления.  | | | | Две системы координатных осей Ox, Oy и Ox’, Oy’ имеют общее начало О и преобразуются одна в дргую поворотом на некоторый угол. Координаты точки А(3; –4) определены относительно первой из них. Вывести формулы преобразования координат, зная, что положительное направление оси Ox’ определено отрезком  . .  | | | | Начало координат перенесено в точку O’(-1; 2), координатные оси повернуты на угол  . Координаты точек M1(3; 2), M2(2; -3), M3(13; -13) определены в новой системе. Вычислить координаты эти же точек в старой системе координат. . Координаты точек M1(3; 2), M2(2; -3), M3(13; -13) определены в новой системе. Вычислить координаты эти же точек в старой системе координат.  | | | | Даны точки A(5; 5), B(2; -1), C(12; -6). Найти их координаты в новой системе, если начало координат перенесено в точку В, а координатные оси повернуты на угол  . .  | | | | Определить старые координаты нового начала и угол 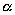 , на который повернуты оси, если формулы преобразвоания координат заданы следующими равенствами: , на который повернуты оси, если формулы преобразвоания координат заданы следующими равенствами: | | | 140.1 |  , ,  ; ; | | | 140.2 |  , ,  ; ; | | | 140.3 |  , ,  ; ;  | | | | Даны точки M1(9; -3), M2(-6; 5). Начало координат перенесено в точку M1, а координатные оси повернуты так, что положительное направление новой оси абсцисс совпадает с направлением отрезка 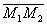 . Вывести формулы преобразования координат. . Вывести формулы преобразования координат.  | | | | Полярная ось полярной системы координат параллельна оси абсцисс декартовой прямоугольной системы и направлена одинаково с нею. Даны декартовы прямоугольные координаты полюса O(1; 2) и полярные координаты точек M1(7;  /2), M2(3; 0), M3(5; - /2), M2(3; 0), M3(5; -  /2), M4(2; 2 /2), M4(2; 2  /3), M5(2; - /3), M5(2; -  /6). Определить координаты этих точек в декартовой прямоугольной системе координат. /6). Определить координаты этих точек в декартовой прямоугольной системе координат.  | | | | Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось направлена по биссектрисе первого координатного угла. Даны полярные координаты точек M1(5;  /4), M2(3; - /4), M2(3; -  /4), M3(1; 3 /4), M3(1; 3  /4), M4(6; -3 /4), M4(6; -3  /4), M5(2; - /4), M5(2; -  /12). Определить декартовы прямоугольные ординаты этих точек. /12). Определить декартовы прямоугольные ординаты этих точек.  | | | | Полярная ось полярной системы координат параллельна оси абсцисс декартовой прямоугольной системы и одинаково с нею направлена. Даны декартовы прямоугольные координаты полюса O(3; 2) и точек M1(5; 2), M2(3; 1), M3(3; 5), M4(  , ,  ), M5( ), M5(  ; 3). Определить полярные координаты этих точек. ; 3). Определить полярные координаты этих точек.  | | | | | |
Часть 2. Уравнение линии










 Глава 7. Преобразование координат
Глава 7. Преобразование координат 



 ,
,  ;
;  ,
,  ;
;  ,
,  ;
;  ,
,  ;
; 

 =600. Координаты точек А(
=600. Координаты точек А( 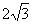 ; -4), B(
; -4), B( 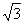 ; 0), C(0;
; 0), C(0; 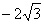 ) определены в новой системе. Вычислить координаты этих же точек в старой системе.
) определены в новой системе. Вычислить координаты этих же точек в старой системе. 

 ,
,  ;
;  ,
,  ;
; 


 .
. 
 . Координаты точек M1(3; 2), M2(2; -3), M3(13; -13) определены в новой системе. Вычислить координаты эти же точек в старой системе координат.
. Координаты точек M1(3; 2), M2(2; -3), M3(13; -13) определены в новой системе. Вычислить координаты эти же точек в старой системе координат. 
 .
. 
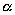 , на который повернуты оси, если формулы преобразвоания координат заданы следующими равенствами:
, на который повернуты оси, если формулы преобразвоания координат заданы следующими равенствами:  ,
,  ;
;  ,
,  ;
;  ,
,  ;
; 
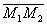 . Вывести формулы преобразования координат.
. Вывести формулы преобразования координат. 
 /2), M2(3; 0), M3(5; -
/2), M2(3; 0), M3(5; - 

 ,
,  ), M5(
), M5(  ; 3). Определить полярные координаты этих точек.
; 3). Определить полярные координаты этих точек. 