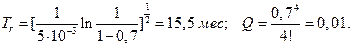Техническое обслуживание резервированных систем

В дальнейшем рассмотрим оптимизацию периодичности замен применительно к резервированным системам. При решении задачи будем предполагать, что надежность резервированной системы H_ЗАД задана на интервале (0, T_r), характеризующем периодичность плановых замен. Надежность нерезервированного блока подчиняется закону распределения Вейбулла.

В случае использования «горячего» резервирования потребное количество блоков m определяется по соотношению

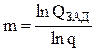
где 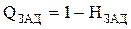- заданная вероятность отказа системы;

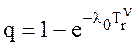- вероятность отказа отдельного блока.

В качестве целевой функции рассмотрим суммарные затраты на эксплуатацию системы

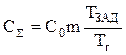
где (m-1) – число резервных блоков; T_ЗАД – время эксплуатации системы; C₀ – стоимость нерезервированной системы.

С учетом потерь при отказах, суммарные затраты примут вид

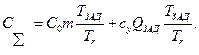
Соответственно для безразмерных затрат имеем

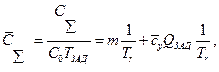
где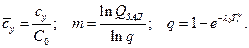

Беря производную по 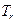, получим

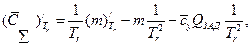
где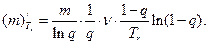

Приравнивая производную нулю, приходим к соотношению

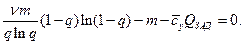
Производя преобразования, найдем

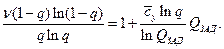
Отсюда

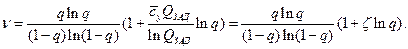
Для высоконадежных систем параметр 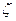будет мал и им можно пренебречь. При этом соотношение упростится

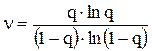
Зависимость ν(q) представлена на рис.4.17

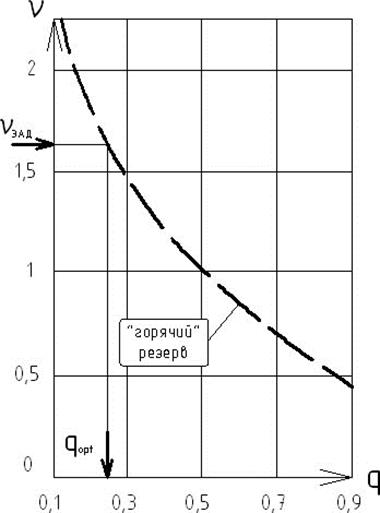
Рис.4.17. Зависимость параметра ν от вероятности отказа q

Знание q_opt позволяет найти оптимальную периодичность замен

,

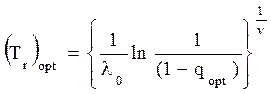а также оптимальную кратность резерва

.

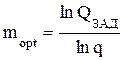При оптимальных значениях вероятности отказа i--го элемента 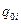реализуются минимальные затраты на обеспечение надежности i-го элемента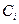

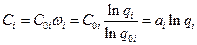, где ;

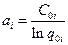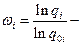кратность резерва, 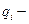вероятность отказа резервированного элемента.

Соответственно суммарные затраты на обеспечение заданных требований к надежности системы будут равны .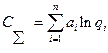

Очевидно значения 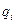целесообразно задавать из условия достижения заданных требований к вероятности отказа системы в целом при минимальных затратах средств .

Для решения этой задачи воспользуемся методом Лагранжа. В рассматриваемом случае функция Лагранжа будет равна

,

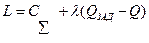где 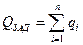; 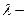неопределенный множитель Лагранжа.

Приравнивая производную 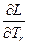нулю и производя необходимые преобразования, получим .

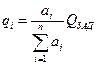Знание 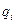позволяет оценить оптимальную кратность резерва 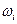и оптимальную периодичность замен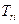

, .

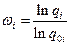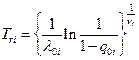Величина 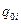оценивается по графику ( рис.4.17 ) в зависимости от 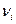, либо по точному соотношению..

.При прогнозировании параметра 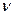можно принять : ,

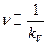где 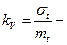коэффициент вариации времени безотказной работы элемента; 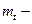среднее время безотказной работы элемента; 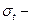среднеквадратическое отклонение времени безотказной работы элемента.

Значения 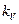оцениваются по статистическим данным для прототипов аналогичных элементов.

В изложенном выше подходе при «горячем» резерве плановой замене подвергается вся система целиком . Однако в составе системы могут находится и работоспособные элементы. Очевидно целесообразно в момент плановой замены производить смену не всего блока, а только вышедших из строя элементов. Эта стратегия возможна для «холодного» резерва. Причем, в случае стареющих элементов, целесообразно производить замену нагруженного элемента, даже если этот элемент не отказал и продолжает выполнять свои функции. Это диктуется необходимостью обеспечения заданных требований, предбявляемых к надежности системы, так как работоспособность у работающего элемента к моменту замены будет хуже, чем у нового. Поэтому в случае возникновения , например, одного отказа, замене должны подвергаться два элемента: один отказавший и один работающий и т д.

В рассматриваемом случае, среднее количество заменяемых элементов M можно оценить по приближенному соотношению

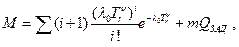
где m - общее число элементов в системе ;

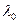- параметр масштаба распределения Вейбулла ;

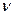- параметр формы распределения Вейбулла ;

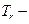периодичность проведения замен ;

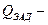заданная вероятность отказа системы.

Производя преобразования, получим

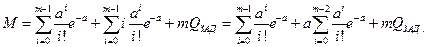
где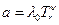

В дальнейшем воспользуемся приближенным соотношением для оценки надежности при « холодном » резервировании [ 5 ].

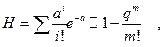(4.41)

где 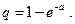(4.42)

Таким образом , приближенно, будем иметь

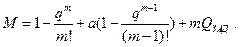
С учетом полученных результатов, выражение для безразмерных затрат на эксплуатацию можно представить в виде

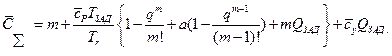
где 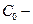стоимость нерезервированной системы ;

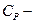затраты на проведение замены одного элемента ;

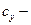величина ущерба при аварийном отказе ;

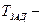заданное время работы системы ;

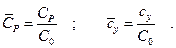
После преобразований, получим

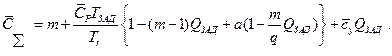
Учитывая малость значени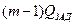й и 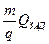по сравнению с единицей,

При проведении дальнейшего анализа ими можно пренебречь. Кроме того будем считать, что для высоконадежных систем величина 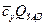существенно меньше m . Таким образом окончательно выражение для безразмерных затрат приближенно можно оценить по соотношению

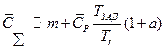
Очевидно оптимальная периодичность замен 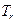удовлетворяет условию

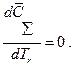
Раскрывая выражение для производной, получим

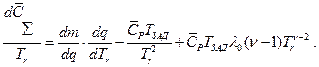
Для нахождения производной 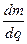прологарифмируем выражение (4.41)

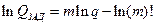
Отсюда

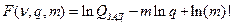
Согласно правилу нахождения производной неявной функции, получим

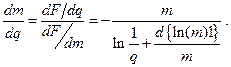
В дальнейшем воспользуемся приближенной оценкой факториала m!

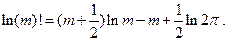
Отсюда

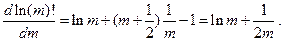
Учитывая соотношение (7.2), найдем

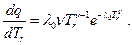
После подстановки полученных результатов в условие оптимальности будем иметь

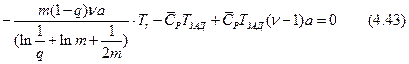
Из соотношения (4.42) получим

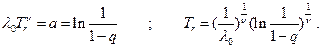
С учетом полученных соотношений уравнение (4.43) примет вид

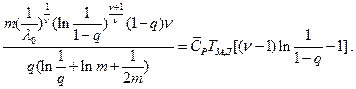
После преобразований окончательно получим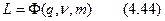

где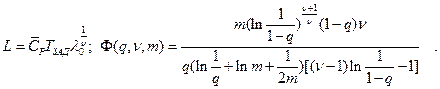

Анализ соотношения для 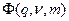показывает, что оптимальное решение существует для значений q , удовлетворяющих условию

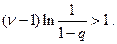
Решая неравенство , приходим к интервалу изменения допустимых

значений q 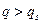где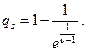

Характер зависимости 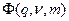по q для 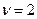и различных m представлен на рис.4.18

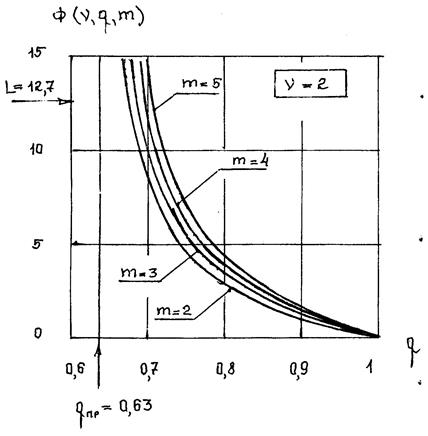
Рис.4.18. Зависимость параметра 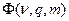от вероятности

отказа нерезервированной системы q для различных кратностей резерва m .

С помощью графика, для заданных значений параметров L и m можно определить оптимальные уровни вероятности отказа нерезервированной системы q . Заметим, что для каждого фиксированного значения L оценки оптимальной вероятности отказа q , в реальном диапазоне изменения кратности резерва m , меняются незначительно. Это позволяет на начальных этапах расчета, когда кратности резерва m неизвестны, в качестве оценки вероятности отказа задавать приближенные значения q , лежащие внутри интервала, соответствующего заданному L и прогнозируемому диапазону изменения m . Знание q позволяет найти оптимальную периодичность замен

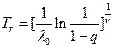и достигаемую при этом вероятность отказа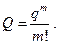

В частности, при исходных данных :

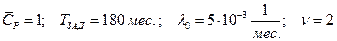
Найдем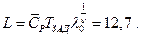

Для рассчитанного L и принятого m=4, по графику получим оптимальную вероятность отказа нерезервированной системы q = 0,7. При этом периодичность замен и вероятность отказа системы соответственно будут равны