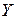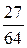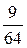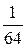Задача 1. Дана система линейных неоднородных алгебраических уравнений
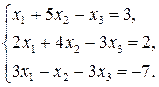
Зная, что система совместна, решим ее:
а) по формулам Крамера; б) с помощью обратной матрицы (матричным методом); в) методом Гаусса.
Решение. а) По формулам Крамера 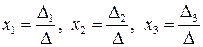 , где
, где
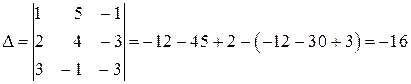 ;
;
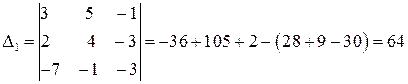 ;
;
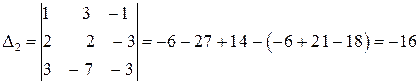 ;
;
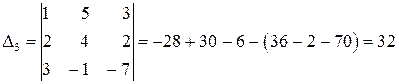 ,
,
находим: 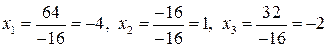 ;
;
б) Для нахождения решения системы с помощью обратной матрицы запишем систему уравнений в матричной форме 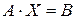 ,
,
где 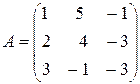 - основная матрица системы,
- основная матрица системы, 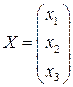 и
и 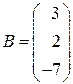 – матрицы-столбцы неизвестных и свободных членов.
– матрицы-столбцы неизвестных и свободных членов.
Решение системы в матричной форме имеет вид 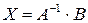 , где
, где 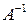 - обратная матрица для невырожденной матрицы
- обратная матрица для невырожденной матрицы 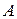 . Матрица
. Матрица 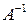 определяется формулой
определяется формулой
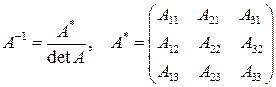 , где
, где 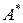 – присоединенная матрица, элементами которой являются алгебраические дополнения
– присоединенная матрица, элементами которой являются алгебраические дополнения 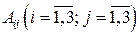 элементов
элементов 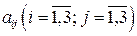 матрицы
матрицы 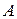 .
.
У нас 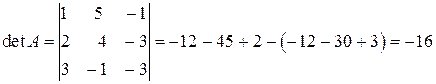 ,
,
т.е. матрица 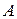 - невырожденная,
- невырожденная,
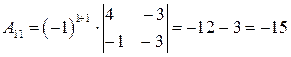 ,
, 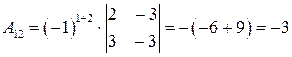 ,
,
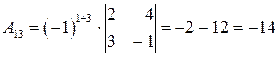 ,
, 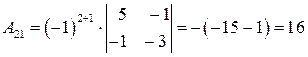 ,
,
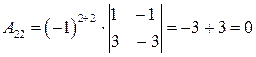 ,
, 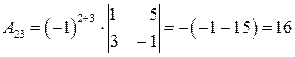 ,
,
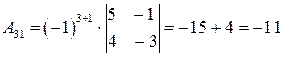 ,
, 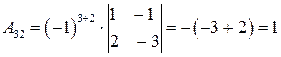 ,
,
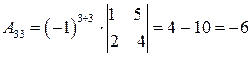 . Тогда
. Тогда 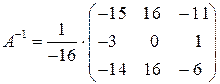 .
.
Решение системы:
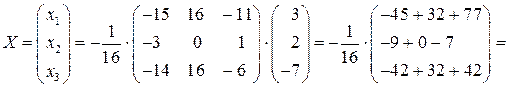
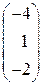 .
.
То есть, 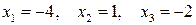 ;
;
в) Решим систему методом Гаусса. Для чего составим расширенную матрицу системы 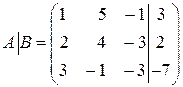 и проведем элементарные преобразования строк: первую строку умножим на 2 и вычтем из второй строки, затем первую строку умножим на 3 и вычтем из третьей строки. После чего разделим элементы третьей строки на (–16).
и проведем элементарные преобразования строк: первую строку умножим на 2 и вычтем из второй строки, затем первую строку умножим на 3 и вычтем из третьей строки. После чего разделим элементы третьей строки на (–16).
Имеем: 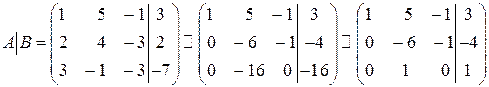 .
.
Полученной матрице, эквивалентной заданной матрице 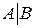 , соответствует система уравнений
, соответствует система уравнений
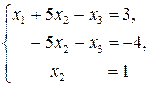 эквивалентная исходной.
эквивалентная исходной.
Из последнего уравнения следует, что 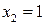 . Подставив значение
. Подставив значение 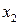 во второе уравнение системы, получим
во второе уравнение системы, получим 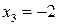 . Подставив значения
. Подставив значения 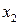 и
и 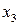 в первое уравнение системы, получим
в первое уравнение системы, получим 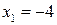 . Итак,
. Итак, 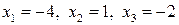 .
.
Проверкой легко убедиться в правильности найденного решения.
Задача 2. Даны вершины треугольника 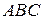 :
: 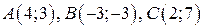 . Найти:
. Найти:
а) уравнение стороны 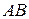 (записать общее и параметрические уравнения);
(записать общее и параметрические уравнения);
б) уравнение высоты 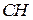 (записать его в отрезках);
(записать его в отрезках);
в) уравнение медианы 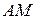 (записать его в каноническом виде);
(записать его в каноническом виде);
г) точку 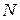 пересечения медианы
пересечения медианы 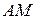 и высоты
и высоты 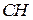 ;
;
д) уравнение прямой, проходящей через вершину 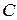 параллельно стороне
параллельно стороне 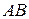 (записать его в нормальном виде);
(записать его в нормальном виде);
е) расстояние от точки 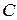 до прямой
до прямой 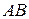 .
.
Решение.
а) Воспользовавшись уравнением прямой, проходящей через две точки, получим уравнение 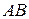 :
: 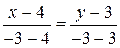 , откуда
, откуда 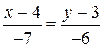 или
или 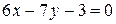 – общее уравнение прямой
– общее уравнение прямой 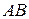 ;
;
и 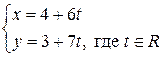 – параметрические уравнения прямой
– параметрические уравнения прямой 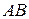 ;
;
б) Угловой коэффициент прямой 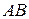
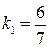 . С учетом перпендикулярности прямых
. С учетом перпендикулярности прямых 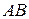 и
и 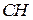 угловой коэффициент высоты
угловой коэффициент высоты 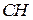
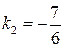
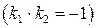 . По точке
. По точке 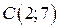 и угловому коэффициенту
и угловому коэффициенту 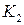 составляем уравнение высоты
составляем уравнение высоты 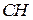 :
: 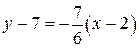 или
или 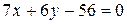 . А в отрезках
. А в отрезках 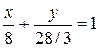 ;
;
в) Находим координаты 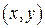 середины
середины 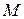 отрезка
отрезка 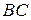 :
: 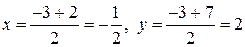 . Теперь по двум известным точкам
. Теперь по двум известным точкам 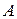 и
и 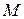 составляем уравнение медианы
составляем уравнение медианы 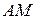 :
:
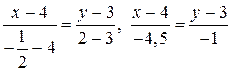 – каноническое уравнение прямой;
– каноническое уравнение прямой;
г) Уравнение медианы 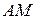
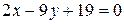 , а высота
, а высота 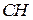
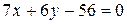 . Для нахождения координат точки
. Для нахождения координат точки 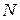 пересечения этих прямых составляет систему уравнений
пересечения этих прямых составляет систему уравнений 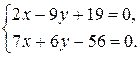 Решая ее, получаем
Решая ее, получаем 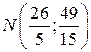 ;
;
д) Так как прямая, проходящая через точку 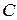 , параллельна стороне
, параллельна стороне 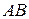 , то их угловые коэффициенты равны
, то их угловые коэффициенты равны 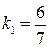 . Тогда по точке
. Тогда по точке 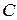 и угловому коэффициенту
и угловому коэффициенту 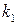 составляем уравнение прямой
составляем уравнение прямой 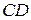 :
: 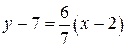 или
или 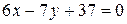 . Чтобы привести его к нормальному виду, введем нормирующий множитель
. Чтобы привести его к нормальному виду, введем нормирующий множитель 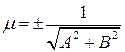 , где знак выбирается противоположным знаку
, где знак выбирается противоположным знаку 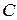 в общем уравнении прямой
в общем уравнении прямой 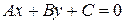 . У нас
. У нас 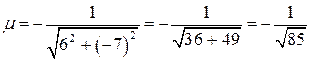 . Тогда нормальное уравнение нашей прямой имеет вид:
. Тогда нормальное уравнение нашей прямой имеет вид: 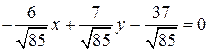 ;
;
е) Расстояние от точки 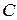 до прямой
до прямой 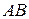 вычисляем по формуле:
вычисляем по формуле:
|
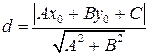 , где точка
, где точка 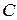 имеет координаты
имеет координаты 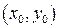 ,
, 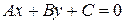 – уравнение заданной прямой. У нас
– уравнение заданной прямой. У нас 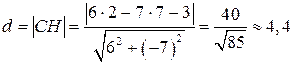 . Решение задачи проиллюстрировано на рисунке.
. Решение задачи проиллюстрировано на рисунке. 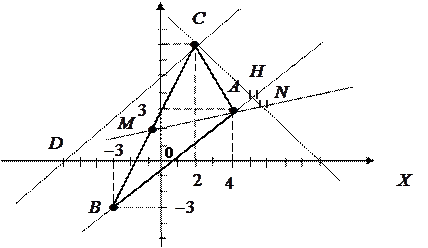
2. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
Задача 3. Найти указанные пределы:
а) 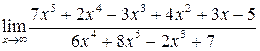 ; б)
; б) 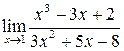 ;
;
в) 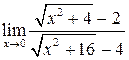 ; г)
; г) 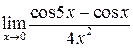 ; д)
; д) 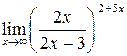 .
.
Решение.
а) 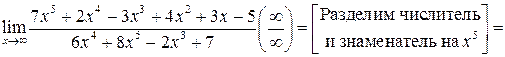
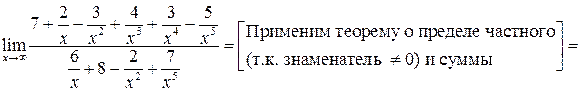
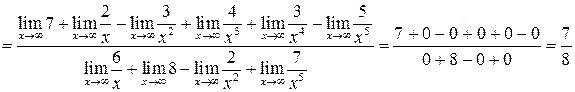 ;
;
б) 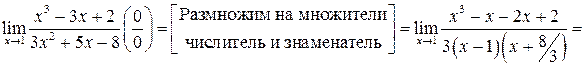
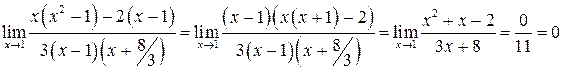 ;
;
в) 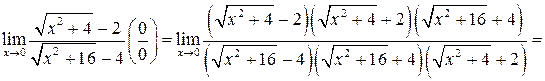
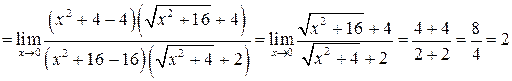 ;
;
г) 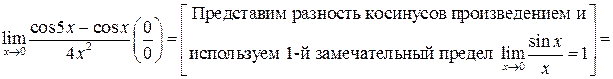
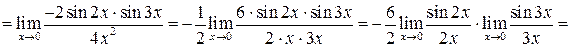
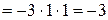 ;
;
д) Здесь используем 2-й замечательный предел 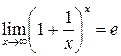 . Получим
. Получим
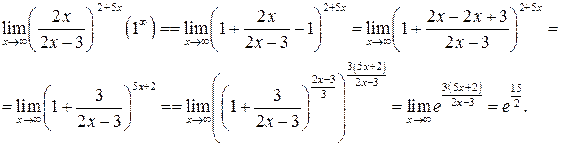
Задача 4. Продифференцировать функции: а) 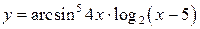 ;
;
б) 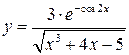 ; в)
; в) 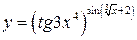 ; г)
; г) 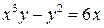 .
.
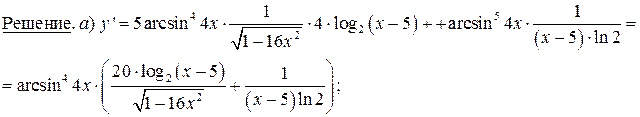
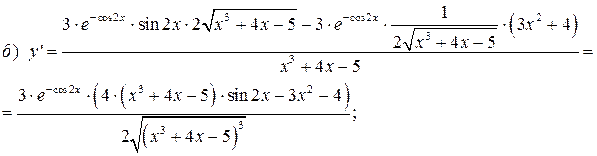
в) Прологарифмируем данную функцию:
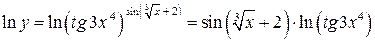 .
.
Тогда 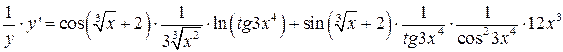 .
.
Выразим 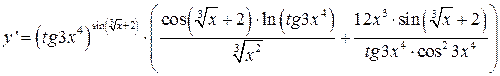 ;
;
г) Продифференцируем, имеем равенство:
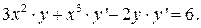 Выразим
Выразим 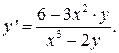
Задача 5. Найти наименьшее и наибольшее значение функции
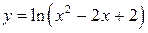 на отрезке
на отрезке 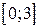 .
.
Решение. Функция 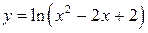 определена на этом отрезке. Найдем критические точки:
определена на этом отрезке. Найдем критические точки: 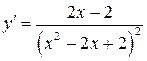 . Если
. Если 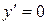 , то
, то 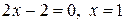 . Найденная точка принадлежит отрезку
. Найденная точка принадлежит отрезку 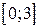 .
. 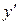 существует для всех
существует для всех 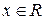 , т.к.
, т.к. 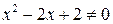 для всех
для всех 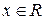 . Найдем значения функции при
. Найдем значения функции при 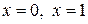 и
и 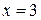 :
: 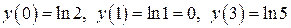 .
.
Следовательно, наименьшего значения данная функция достигает в точке 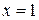 :
: 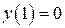 , а наибольшего – в точке
, а наибольшего – в точке 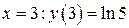 .
.
Задача 6. Исследовать функцию 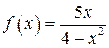 и построить её график.
и построить её график.
Решение. Общая схема построения графика функции:
1) находим область определения функции;
2) исследуем функцию на периодичность, четность или нечетность;
3) исследуем функцию на монотонность и экстремум;
4) находим промежутки выпуклости и точки перегиба;
5) отыскиваем асимптоты графика функции;
6) для уточнения хода графика функции находим точки пересечения его с осями координат;
7) строим график функции.
В нашем случае имеем:
1. Областью определения 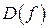 функции является множество
функции является множество
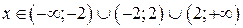 .
.
2. Функция нечетная, т.к. область ее определения симметрична относительно начала координат и выполнено условие 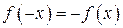 . Функция непериодическая.
. Функция непериодическая.
3. Находим 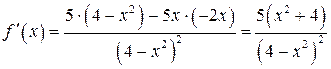 . Видим, что
. Видим, что
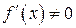 для всех
для всех 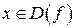 и
и 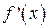 не существует, если
не существует, если 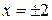 . Эти
. Эти
точки разбивают область определения функции на промежутки
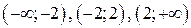 . Исследуем знак производной
. Исследуем знак производной 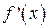 на этих
на этих
промежутках. Результаты заносим в таблицу
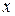 | 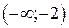 | 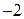 | 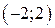 | 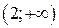 | |
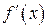 | + | 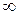 | + | 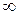 | + |
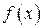 | возрастает | 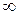 | возрастает | 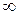 | возрастает |
Из таблицы видно, что функция всюду возрастает на 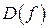 и точки локального минимума и максимума не имеет.
и точки локального минимума и максимума не имеет.
4. Находим 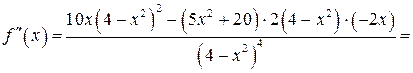
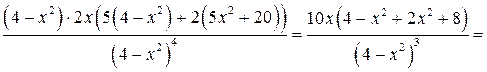
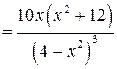 . Точками возможного перегиба являются точки
. Точками возможного перегиба являются точки
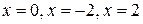 . Они разбивают область определения функции на
. Они разбивают область определения функции на
промежутки 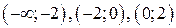 . Исследуем знак
. Исследуем знак 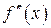 на этих
на этих
промежутках. Результаты исследования заносим в таблицу
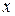 | 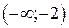 | 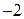 | 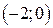 | 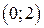 | 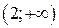 | ||
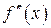 | + | 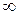 | – | + | 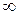 | – | |
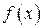 | выпукла вниз | 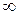 | выпукла вверх | перегиб | выпукла вниз | 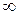 | выпукла вверх |
5. Вертикальными асимптотами являются 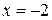 и
и 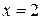 , причем
, причем
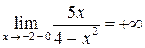 ,
, 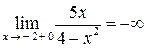 ,
, 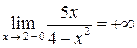 ,
, 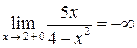 .
.
Ищем наклонную асимптоту 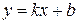 . Так как
. Так как 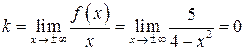 ,
,
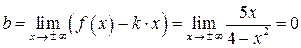 , то
, то 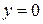 – горизонтальная асимптота.
– горизонтальная асимптота.
 6. Находим точки пересечения графика с осями координат. Это точка
6. Находим точки пересечения графика с осями координат. Это точка 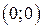 .
.
7. Строим график функции
Задача 7. Найти следующие интегралы.
а) 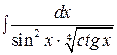 ; б)
; б) 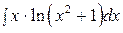 ; в)
; в) 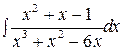 ;
;
г) 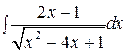 ; д)
; д) 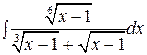 ; е)
; е) 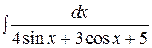 .
.
Результат интеграла а) проверить дифференцированием.
Решение . а) 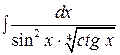 . Произведем замену переменной
. Произведем замену переменной 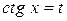 . Дифференцируем это равенство
. Дифференцируем это равенство 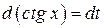 или
или 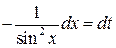 , тогда
, тогда 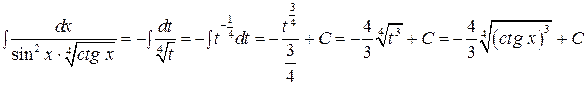
Проверка: 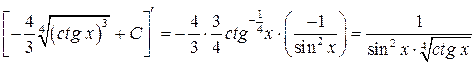 ;
;
б) 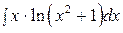 .
.
Воспользуемся формулой интегрирования по частям:
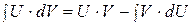 . Положим
. Положим 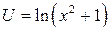 ,
, 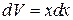 .
.
Тогда 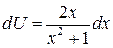 ,
, 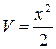 .
.
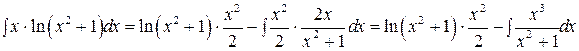 .
.
Отдельно вычислим 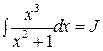 . Разделим
. Разделим 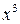 на
на 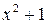 по правилу деления
по правилу деления 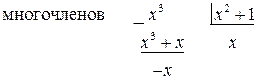 Тогда
Тогда 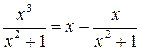 .
.
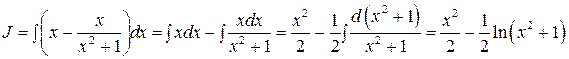 .
.
Исходный интеграл равен
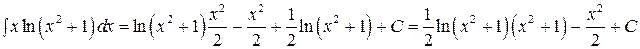 в)
в) 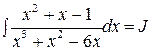 .
.
Разложим правильную рациональную дробь (степень числителя «2» меньше степени знаменателя «3») на сумму простейших дробей:
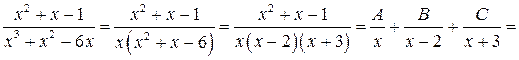
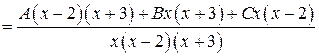
Приравниваем числители первой и последней дробей
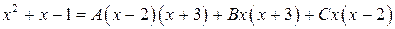
Сгруппируем члены с одинаковыми степенями:
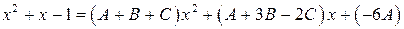 .
.
Сравнивая коэффициенты при одинаковых степенях 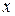 , получаем систему уравнений:
, получаем систему уравнений:
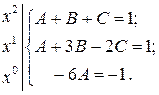
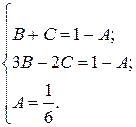
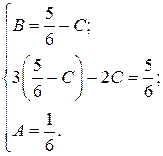
Þ 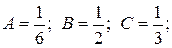 Þ
Þ
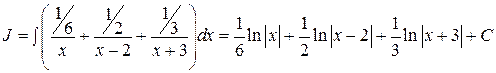 ;
;
г) 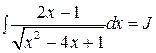 . Выделим полный квадрат в выражении, стоящем под корнем
. Выделим полный квадрат в выражении, стоящем под корнем 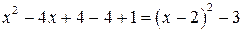 и сделаем замену переменной
и сделаем замену переменной
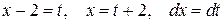 .
.
Тогда
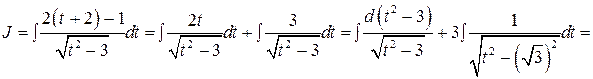
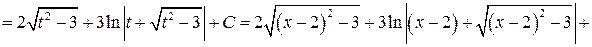
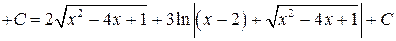 ;
;
д) 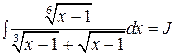 .
.
Под интегралом стоит иррациональная функция. Приведем ее к рациональной с помощью подстановки 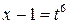 , где
, где 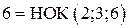 - наименьшее общее кратное показателей корней. Тогда
- наименьшее общее кратное показателей корней. Тогда 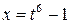 ,
, 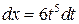 .
.
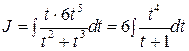 . Разделим “уголком” числитель
. Разделим “уголком” числитель 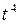 на знаменатель
на знаменатель 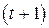 . Получим
. Получим 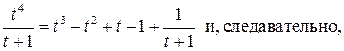
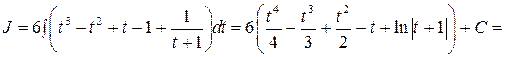
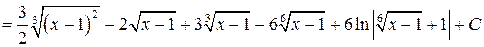 .
.
е) 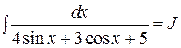 .
.
Интегралы вида 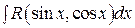 , где
, где 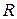 – рациональная функция, приводятся к интегралам от рациональной функции нового аргумента с помощью универсальной тригонометрической подстановки
– рациональная функция, приводятся к интегралам от рациональной функции нового аргумента с помощью универсальной тригонометрической подстановки 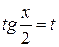 . В результате имеем
. В результате имеем 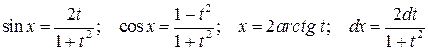 .
.
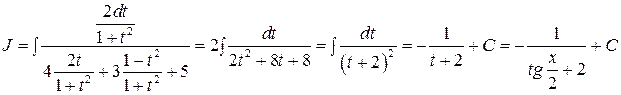 .
.
Задача 8. Найти площадь фигуры, ограниченной графиками функции 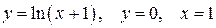 . Сделать схематический чертеж.
. Сделать схематический чертеж.
Решение. Площадь фигуры, ограниченной графиком функции 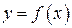 ,
,
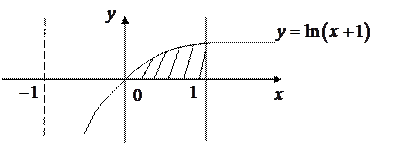 прямыми
прямыми 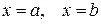 и осью
и осью 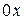 , вычисляется по формуле
, вычисляется по формуле 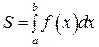 .
.
Построим фигуру.
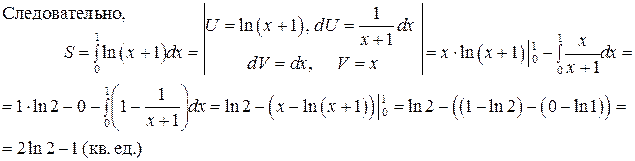
3. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Задача 9. Проверить, удовлетворяет ли уравнению 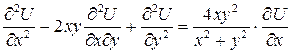 функция
функция 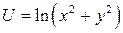 .
.
Решение. Находим частные производные первого и второго порядка:
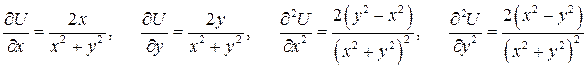 ,
,
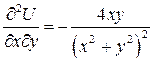 . Подставляем полученные значения производных в левую часть исходного уравнения:
. Подставляем полученные значения производных в левую часть исходного уравнения: 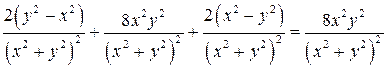 .
.
В правой части имеем: 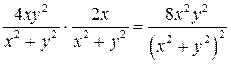 .
.
Сравнивая полученные результаты, видно, что данная функция удовлетворяет исходному уравнению.
Задача 10. Исследовать на экстремум функцию 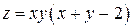
Решение. Находим первые частные производные данной функции:
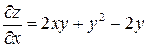 ,
, 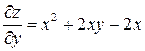 .
.
Приравнивая их к нулю, получаем систему уравнений:
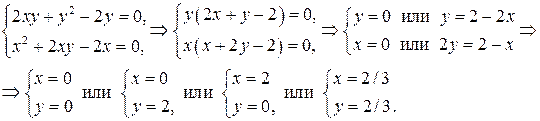
Получили стационарные точки данной функции: 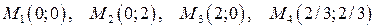 . Выясним, какие из этих точек являются точками экстремума. Для этого вначале найдем вторые частные производные данной функции:
. Выясним, какие из этих точек являются точками экстремума. Для этого вначале найдем вторые частные производные данной функции:
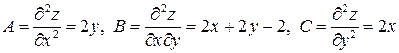 .
.
Составим определитель 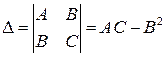 .
.
Подставляя в 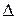 координаты стационарных точек и используя достаточные условия экстремума, имеем: для точки
координаты стационарных точек и используя достаточные условия экстремума, имеем: для точки 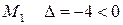 , т.е. экстремума нет, для точки
, т.е. экстремума нет, для точки 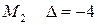 , т.е. экстремума нет, для точки
, т.е. экстремума нет, для точки 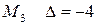 , т.е. экстремума нет, для точки
, т.е. экстремума нет, для точки 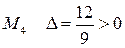 и
и 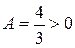 , т.е. имеем точку локального минимума функции, в которой
, т.е. имеем точку локального минимума функции, в которой 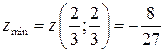 .
.
4. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Задача 11. Найти общее решение (общий интеграл) дифференциального уравнения (особые решения не рассматривать) 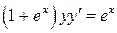 .
.
Решение. Заменим 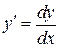 .
. 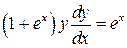 . Это уравнение с разделяющимися переменными. Нужно умножить или разделить обе части уравнения на такое выражение, чтобы в одну часть уравнения входило только
. Это уравнение с разделяющимися переменными. Нужно умножить или разделить обе части уравнения на такое выражение, чтобы в одну часть уравнения входило только 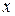 , а в другую – только
, а в другую – только  , и затем проинтегрировать обе части. Умножим последнее уравнение на
, и затем проинтегрировать обе части. Умножим последнее уравнение на 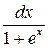 .
. 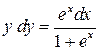 . Интегрируем
. Интегрируем 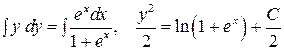 .
.
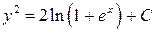 – общий интеграл.
– общий интеграл.
Задача 12. Найти частное решение (частный интеграл) дифференциального уравнения, удовлетворяющее начальному условию
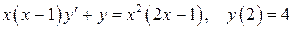 .
.
Решение. Разделим обе части уравнения на 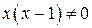 .
.
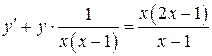 (*). Это линейное дифференциальное уравнение первого порядка. Решение ищем в виде
(*). Это линейное дифференциальное уравнение первого порядка. Решение ищем в виде 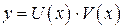 , тогда
, тогда 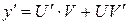 . Подставляем
. Подставляем  и
и 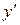 в уравнение (*)
в уравнение (*)
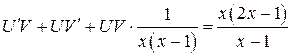 ,
, 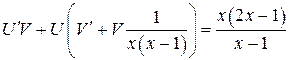 (**)
(**)
Функцию 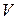 находим из условия
находим из условия 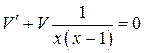
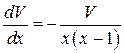 – это уравнение с разделяющимися переменными.
– это уравнение с разделяющимися переменными.
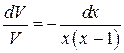 . Интегрируем
. Интегрируем 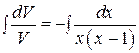 ,
,
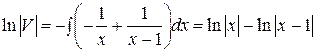 ,
, 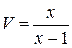 . В качестве функции
. В качестве функции 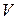 взяли одно частное решение
взяли одно частное решение 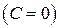 . Подставляем
. Подставляем 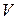 в уравнение (**), получаем
в уравнение (**), получаем
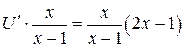 ,
, 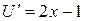 , тогда
, тогда 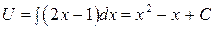 .
.
Следовательно, общее решение исходного уравнения
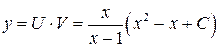 . Используя начальное условие
. Используя начальное условие 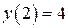 ,
,
найдем 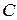 :
: 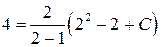 , откуда
, откуда 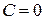 .
.
Частное решение исходного уравнения будет 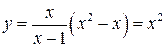 .
.
Задача 13. Найти общее решение дифференциального уравнения, допускающего понижение порядка 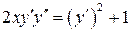 .
.
Решение. Уравнение не содержит искомой функции. Введем новую функцию 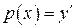 , тогда
, тогда 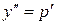 . Исходное уравнение примет вид:
. Исходное уравнение примет вид: 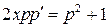 .
.
Это уравнение с разделяющимися переменными 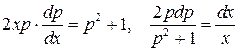 .
.
Интегрируем 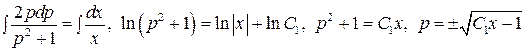 .
.
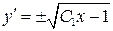 .
. 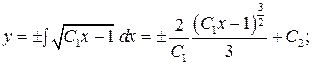
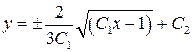 – общее решение.
– общее решение.
5. РЯДЫ
Задача 14. Исследовать на сходимость заданный числовой ряд с положительными членами, используя достаточные признаки сходимости.
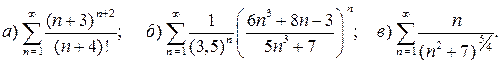
Решение. а) Используем признак Даламбера:
если члены ряда 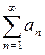 положительны и
положительны и 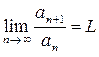 , то
, то
при L < 1 ряд сходится, при L > 1 ряд расходится,
при L = 1 ряд нужно исследовать другими методами.
Записываем общий член ряда 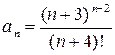 . Член
. Член 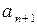 получается из
получается из 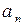 заменой номера n на номер n + 1:
заменой номера n на номер n + 1: 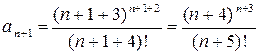 .
.
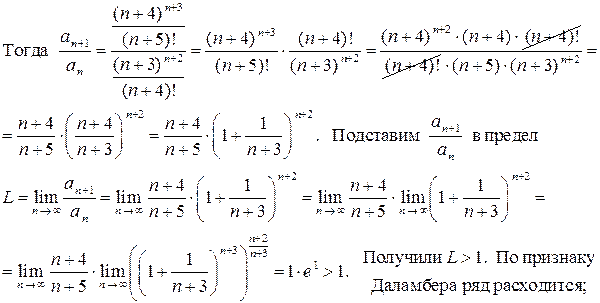
б) Используем радикальный признак Коши :
если члены ряда 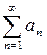 положительны и
положительны и 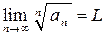 , то
, то
при L < 1 ряд сходится, при L > 1 ряд расходится,
при L = 1 ряд нужно исследовать другими методами.
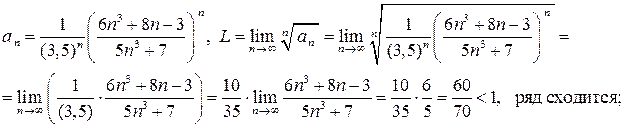
в) Используем интегральный признак Коши. Пусть члены ряда 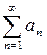 убывают, функция f (x) непрерывна на [a;+¥) и
убывают, функция f (x) непрерывна на [a;+¥) и 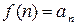 . Тогда
. Тогда
если несобственный интеграл 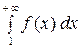 сходится, то ряд
сходится, то ряд 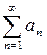 сходится,
сходится,
если несобственный интеграл 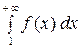 расходится, то ряд
расходится, то ряд 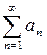 расходится.
расходится.
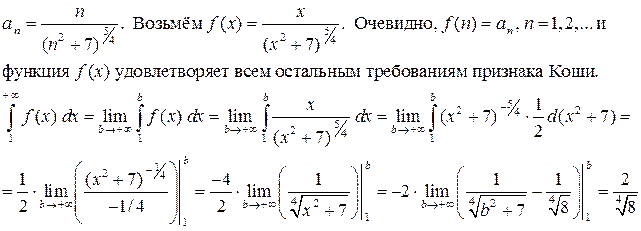
Несобственный интеграл сходится (имеет конечное значение), следовательно, ряд сходится.
Задача 15. Найти область сходимости функционального ряда 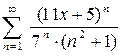 .
.
Решение. 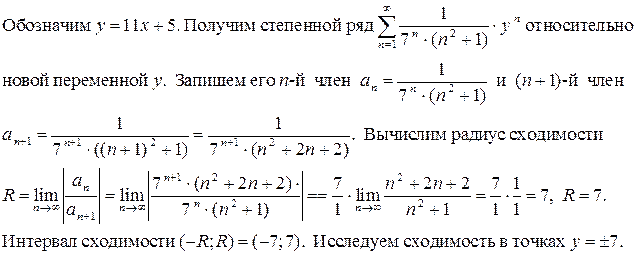
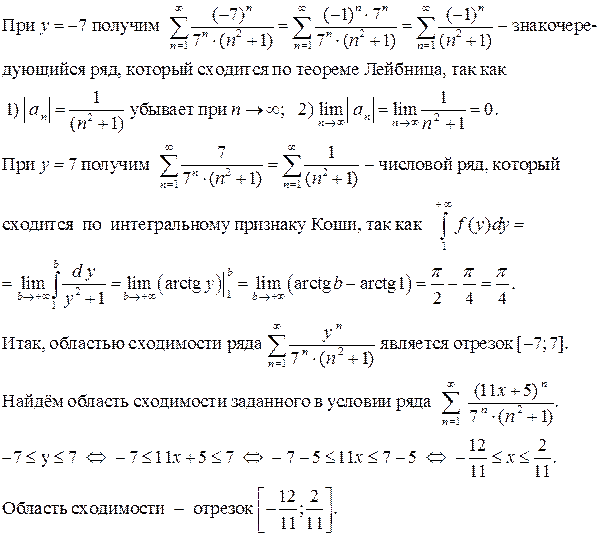
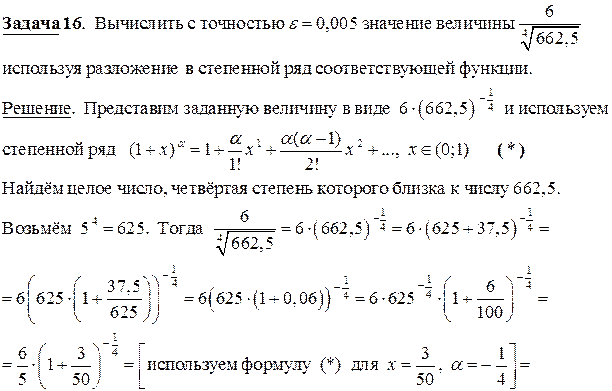
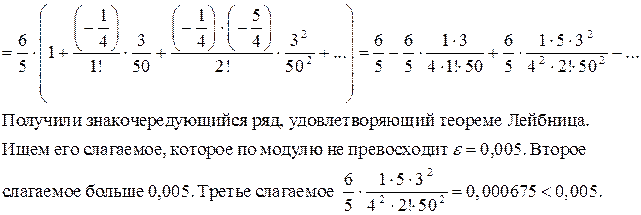
По следствию из теоремы Лейбница, остаток ряда, начинающийся с третьего слагаемого, не превосходит числа e = 0,005 и, следовательно, сумма первых двух слагаемых 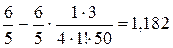 отличается от суммы ряда не более чем на 0,005. Таким образом,
отличается от суммы ряда не более чем на 0,005. Таким образом, 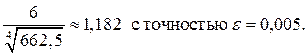
6. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Задача 17. Имеется 6 одинаковых шаров, занумерованных числами 1, 2, 3, 4, 5, 6. Наудачу раскладываем эти шары в 3 коробки по 2 шара. Найти вероятность того, что в каждой коробке окажется один нечётный шар и один чётный.
Решение. Опыт состоит в том, что 6 шаров наудачу раскладываем по 2 шара в 3 коробки. Все исходы опыта равновозможны и их число n конечно. Следовательно, можем применить классическую формулу вероятности 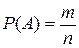 , где А – событие, состоящее в том, что в каждой коробке окажется один нечётный шар и один чётный, а m – число всех исходов, благоприятствующих событию А.
, где А – событие, состоящее в том, что в каждой коробке окажется один нечётный шар и один чётный, а m – число всех исходов, благоприятствующих событию А.
Найдём n – число всех исходов опыта. Выбрать 2 шара из 6-ти в I-ю коробку можно 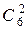 способами. Из оставшихся 4 шаров выбрать 2 шара во II-ю коробку можно
способами. Из оставшихся 4 шаров выбрать 2 шара во II-ю коробку можно 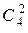 способами. Оставшиеся после этого 2 шара попадут в III-ю коробку (
способами. Оставшиеся после этого 2 шара попадут в III-ю коробку ( 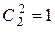 ). Число всех исходов опыта равно
). Число всех исходов опыта равно 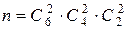 . По формуле
. По формуле 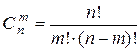 вычислим
вычислим 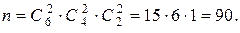
Найдём m – число исходов, благоприятствующих событию А. Выбрать нечётный шар в I-ю коробку можно 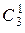 способами, чётный –
способами, чётный – 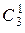 способами. Следовательно, число всех благоприятствующих пар шаров для I-й коробки равно
способами. Следовательно, число всех благоприятствующих пар шаров для I-й коробки равно 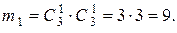 Обозначим сказанное схематично:
Обозначим сказанное схематично:
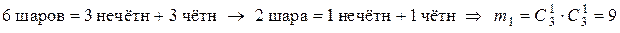 .
.
Аналогично найдём число благоприятствующих пар шаров для II-й коробки из оставшихся 4 шаров:
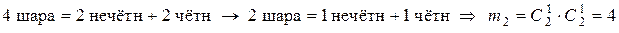 .
.
Для III-й коробки
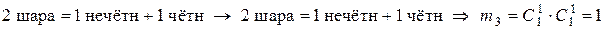 .
.
Тогда 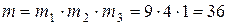 ,
, 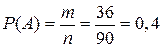 .
.
Искомая вероятность равна 0,4.
Задача 18. Три студента сдают экзамен. Для них приготовлены три билета: №1, №2, №3. Первый студент наудачу возьмёт любой билет, второй выберет наудачу один из двух оставшихся, третий заберёт оставшийся. Для каждого из студентов найти вероятность извлечь билет №1.
Решение. Пусть А1, А2, А3 – события, состоящие в том, что соответственно 1-й, 2-й и 3-й студент извлечёт билет №1. Требуется найти 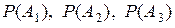 .
.
Очевидно, что 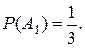 Найдём
Найдём 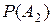 . Первый студент взял один билет. Второму осталось два билета. Обозначим гипотезы:
. Первый студент взял один билет. Второму осталось два билета. Обозначим гипотезы:
Н1 – билет №1 уже извлечён; Н2 – билет №1 ещё не извлечён.
Н1, Н2 – полная группа событий ( сумма этих событий – достоверное событие и они не могут произойти одновременно). Следовательно, по формуле полной вероятности 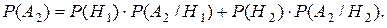
Очевидно, что 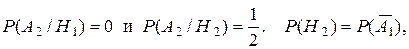 так как гипотеза Н2 означает что 1-й студент не взял билет №1. Итак,
так как гипотеза Н2 означает что 1-й студент не взял билет №1. Итак, 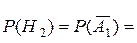
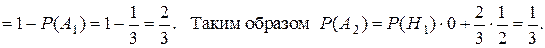
Найдём Р(А3). 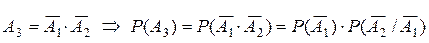 .
.
Уже вычислено 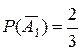 . Условная вероятность
. Условная вероятность 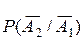 – это вероятность того, что 2-й студент не взял билет №1 при условии, что 1-й студент не взял билет №1, то есть вероятность не взять билет №1 из двух билетов, среди которых есть этот №1. Получаем
– это вероятность того, что 2-й студент не взял билет №1 при условии, что 1-й студент не взял билет №1, то есть вероятность не взять билет №1 из двух билетов, среди которых есть этот №1. Получаем 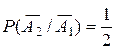 . В результате
. В результате 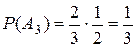 .
.
Все искомые вероятности найдены: 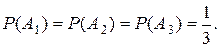
Задача 19. MN – средняя линия треугольника АВС, MN P АВ. На треугольник АВС наудачу поставлены три точки. Случайная величина Х равна числу точек, попавших на треугольник MBN. Построить ряд распределения этой случайной величины.
Решение. Случайная величина Х может принимать значения х1 = 0, х2 = 1,
х3 = 2, х4 = 3. Найдем вероятность появления каждого из этих значений.
 Так как MN – средняя линия D АВС, то
Так как MN – средняя линия D АВС, то 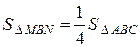 .
.
Вероятность того, что точка, наудачу поставленная на
D АВС, попадёт на D MВN равна 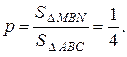
Это испытание (наудачу ставим точку на D АВС) повторяем 3 раза. Вероятность того, что в n = 3 испытаниях событие (попадание точки на D MВN ) произойдёт ровно k раз вычислим по формуле Бернулли:
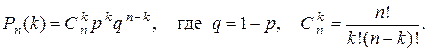
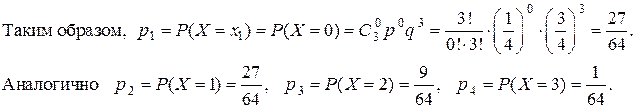
|
Построим искомый ряд распределения .
Задача 20. Задан ряд распределения дискретной случайной величины Х. Найти неизвестный параметр С, математическое ожидание M(X), дисперсию D(X), среднее квадратическое отклонение 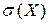 и вероятность P(a < X < b).
и вероятность P(a < X < b).
|
|
Решение. Сумма вероятностей всех возможных значений Х равна единице. Следовательно, 0,4 + С + 0,35 + 0,1 = 1, С = 0,15.
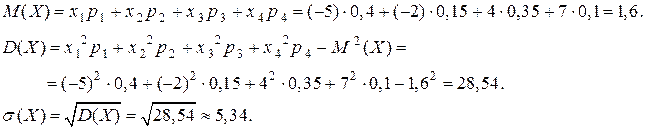
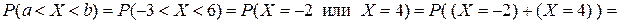
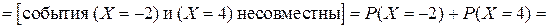
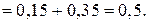 Таким образом найдены
Таким образом найдены
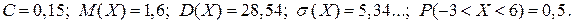
Задача 21. Задана плотность распределения непрерывной случайной величины Х. Найти неизвестный параметр С, математическое ожидание M(X), дисперсию D(X), среднее квадратическое отклонение 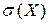 и вероятность P(a < X < b).
и вероятность P(a < X < b). 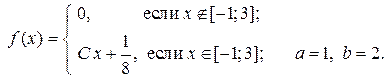
Решение. Плотность распределения непрерывной случайной величины удовлетворяет условию 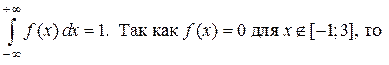
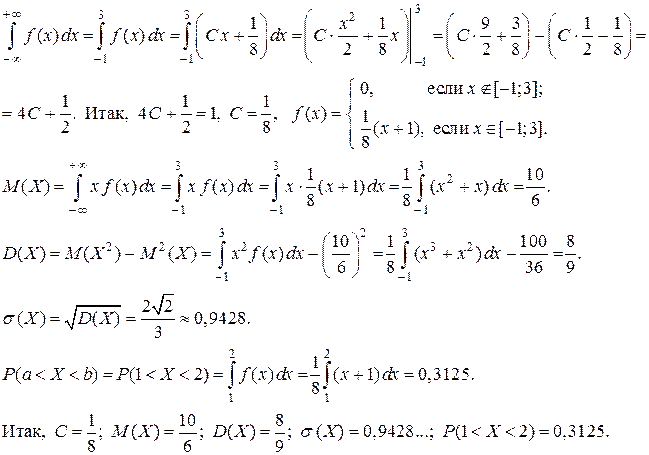
СОДЕРЖАНИЕ
Введение 3
Общие рекомендации студентам по работе над контрольной работой 3
Вопросы к экзамену по курсу “Высшая математика” 4
Литература 9
Задания для контрольных работ 9
Методические указания к решению типовых задач 23
Тема 1. Линейная алгебра и аналитическая геометрия 23
Тема 2. Дифференциальное и интегральное исчисления 27
Тема 3. Функции нескольких переменных 34
Тема 4. Дифференциальные уравнения 35
Тема 5. Ряды 37
Тема 6. Теория вероятностей 40