Теория вероятностей и математическая статистика»
| Вариант 1 | Вариант 2 |
Задание 1. Непрерывная случайная величина 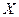 задана своей функцией распределения задана своей функцией распределения 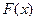 . Найти плотность распределения вероятностей . Найти плотность распределения вероятностей 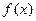 и определить вероятность того, что данная величина примет значение из указанного интервала. и определить вероятность того, что данная величина примет значение из указанного интервала. | |
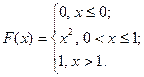 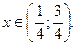 | 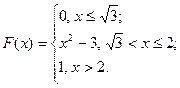 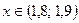 |
Задание 2. Непрерывная случайная величина 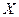 задана своей плотностью распределения задана своей плотностью распределения 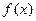 . Найти функцию распределения вероятностей . Найти функцию распределения вероятностей 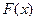 , построить графики обеих функций. , построить графики обеих функций. | |
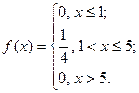 | 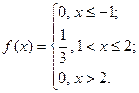 |
Задание 3. Непрерывная случайная величина 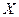 задана своей плотностью распределения задана своей плотностью распределения 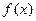 . Найти моду, математическое ожидание и медиану этой случайной величины. (Указание: построить график . Найти моду, математическое ожидание и медиану этой случайной величины. (Указание: построить график 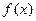 ) ) | |
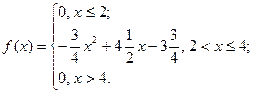 | 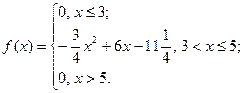 |
Задание 4. Непрерывная случайная величина задана плотностью распределения вероятностей 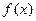 . Найти её математическое ожидание, дисперсию и среднее квадратическое отклонение. . Найти её математическое ожидание, дисперсию и среднее квадратическое отклонение. | |
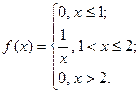 | 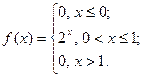 |
Задание 5. Система двух непрерывных случайных величин 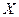 и и 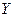 задана функцией распределения задана функцией распределения 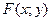 . Найти плотность распределения. . Найти плотность распределения. | |
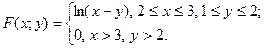 | 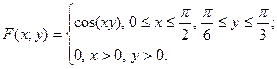 |
Задание 6. Система двух непрерывных случайных величин 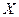 и и 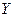 задана функцией распределения задана функцией распределения 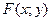 . Найти вероятность попадания точки . Найти вероятность попадания точки 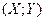 в указанный прямоугольник. в указанный прямоугольник. | |
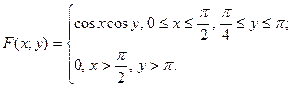 | 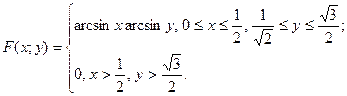 |
9. Аудиторная контрольная работа по теме «Теория вероятностей и математическая статистика:
Вариант № 1.
1. В ящике 10 шаров: 4 красных и 6 белых. Из ящика вынимают сразу 6 шаров. Найти вероятность того, что среди них 4 красных шара и 2 белых.
2. В партии из 12 изделий 7 стандартных. Найти вероятность того, что среди 3 наугад взятых изделий нет ни одного стандартного.
3. Прибор содержит 3 независимо работающих устройства, поломка каждого из которых приводит к выходу из строя всего прибора. Вероятности выхода из строя каждого из этих устройств соответственно равны: 0,2, 0,1 и 0,35. Найти вероятность выхода из строя прибора.
4. Вероятность поражения цели одним из двух орудий равна 0,8, а другим – 0,7. Какова вероятность того, что при залпе цель будет поражена хотя бы из одного орудия?
Вариант № 2.
1. В ящике 10 шаров: 7 красных и 3 белых. Из ящика вынимают сразу 5 шаров. Найти вероятность того, что среди них 3 красных шара и 2 белых.
2. В партии из 12 изделий 8 стандартных. Найти вероятность того, что среди 2 наугад взятых изделий нет ни одного стандартного.
3. Прибор содержит 3 независимо работающих устройства. Поломка каждого устройства приводит к выходу из строя всего прибора. Вероятности выхода из строя каждого из этих устройств соответственно равны: 0,2, 0,3 и 0,35. Найти вероятность безаварийной работы прибора.
4. Вероятность поражения цели одним из двух орудий равна 0,8, а другим – 0,7. Какова вероятность того, что при залпе цель не будет поражена ни одним из орудий?
Вариант № 3.
1. В ящике 12 шаров: 6 красных и 6 белых. Из ящика вынимают сразу 6 шаров. Найти вероятность того, что среди них 4 красных шара и 2 белых.
2. В партии из 10 изделий 7 стандартных. Найти вероятность того, что среди 2 наугад взятых изделий есть хотя бы одно нестандартное.
3. Прибор содержит 3 независимо работающих устройства. Поломка каждого устройства приводит к выходу из строя всего прибора. Вероятности безаварийной работы в данный момент каждого из этих устройств соответственно равны: 0,8, 0,9 и 0,95. Найти вероятность выхода из строя прибора.
4. Вероятность поражения цели одним из двух орудий равна 0,8, а другим – 0,7. Какова вероятность того, что при залпе цель будет поражена обоими орудиями?
Вариант № 4.
1. В ящике 12 шаров: 8 красных и 4 белых. Из ящика вынимают сразу 5 шаров. Найти вероятность того, что среди них 2 красных шара и 3 белых.
2. В партии из 10 изделий 8 стандартных. Найти вероятность того, что среди 3 наугад взятых есть хотя бы одно нестандартное.
3. Прибор содержит 3 независимо работающих устройства. Поломка каждого устройства приводит к выходу из строя всего прибора. Вероятности выхода из строя каждого из этих устройств соответственно равны: 0,1 , 0,15 и 0,05. Найти вероятность выхода из строя прибора.
4. Вероятность поражения цели одним из двух орудий равна 0,8, а другим – 0,9. Какова вероятность того, что при залпе цель будет поражена только из одного орудия?
Вариант № 5.
1. В ящике 10 шаров: 6 красных и 4 белых. Из ящика вынимают сразу 4 шара. Найти вероятность того, что среди них 3 красных шара и 1 белый.
2. В партии из 10 изделий 8 стандартных. Найти вероятность того, что среди 2 наугад взятых изделий нет ни одного нестандартного.
3. Прибор содержит 3 независимо работающих устройства. Поломка каждого устройства приводит к выходу из строя всего прибора. Вероятности выхода из строя каждого из этих устройств соответственно равны: 0,05, 0,15 и 0,2. Найти вероятность выхода из строя прибора.
4. Вероятность поражения цели одним из двух орудий равна 0,8, а другим – 0,9. Какова вероятность того, что при залпе цель будет поражена хотя бы из одного орудия?
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторной работе №5 по математике
АППРОКСИМАЦИЯ ЭМПИРИЧЕСКИХ ДАННЫХ.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ.
ЦЕЛЬ РАБОТЫ: С помощью программных пакетов Excel, Mathcad по заданным парам значений переменных получить наилучшие параметры эмпирической формулы методом наименьших квадратов.
