В уравнение вращательного движения цилиндра относительно точки О

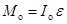(64)

входит момент силы тяжести

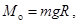
а плечо силы натяжения ленты равно нулю. Моменты инерции цилиндра отно­сительно оси, проходящей через точку О, по теореме Штейнера (59)

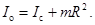
Ускорение разматывания 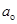по своему смыслу равно тангенциальному ускоре­нию поверхности цилиндра, которое в свою очередь равно 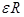(19),

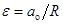
Подставляя полученные выражения для 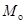, 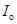и 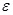в уравнение (64) получаем

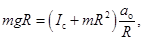
то есть

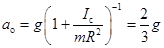
и

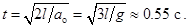
Обратите внимание на то, что в этом способе движение цилиндра описы­вается только уравнением вращательного движения относительно точки О (64); уравнение поступательного движения (62) не используется. Поверхность ци­линдра покоится относительно ленты, которая на него намотана. В частности, в точке О линия касания цилиндра покоится относительно ленты, цилиндр со­вершает только вращательное движение вокруг этой линии, называемой мгно­венной осью вращения, а сама эта линия опускается вниз с ускорением .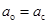

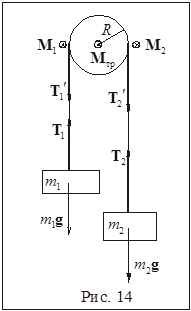
8. Через блок переброшена легкая нерастяжимая нить, к концам которой прикреплены грузы массам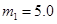и кг и 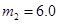кг. Масса блока 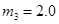кг, радиус блока 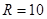см, момент сил трения в блоке 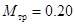Н. Определить ускорение системы и натяжение нити.

Решение:

Система состоит из трех тел (см. рис. 14), два из которых (грузы) совер­шают поступательное движение, а блок – вращательное:

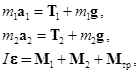
где 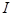– момент инерции блока, 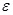– его угловое ускорение, 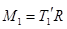и 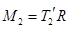– моменты сил натяжения нити. Считая блок однородным цилин­дром, положим (57)

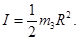
Легкость нити даёт основание считать её натяжение одинаковым по одну сто­рону блока:

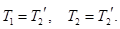
Однако 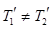вследствие массивности блока и наличия момента сил трения. Нерастяжимость нити означает равенство по величине ускорений грузов:

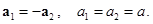
Угловое ускорение блока 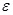связано с тангенциальным ускорением поверхности блока 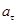соотношением (19) 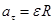. Тангенциальное ускорение блока 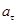равно по величине ускорению грузов, 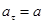. Поэтому

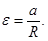
Моменты сил 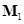и 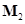направлены вдоль оси вращения в противоположные стороны. Так как 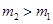, момент сил трения 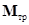направлен против 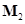. Проек­тируя уравнение вращательного движения блока на ось его вращения, получаем

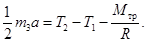
Проектируем уравнения поступательного движения грузов на вертикальную ось:

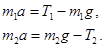
Решая полученную систему трёх уравнений, находим результат:

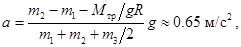
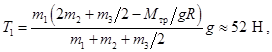
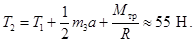
Сравните это решение с решением задачи 3.

9. Кинетическая энергия вращающегося маховика равна 1кДж. Под дей­ствием постоянного тормозящего момента сил маховик начал замедлять свое вращение и, сделав 80 оборотов, остановился. Определить момент сил тормо­жения.

Решение:

Обладая известной из условия задачи кинетической энергией вращения 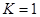кДж, маховик имел угловую скорость 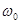, определяемую соотношением (60):

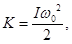
где 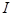– момент инерции маховика. Согласно уравнению вращательного движе­ния (50)

,

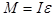постоянный по условию тормозящий момент сил 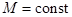приводит к замедле­нию вращения с постоянным угловым ускорением 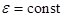. В этом случае формула (21) уменьшения угловой скорости

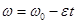
до остановки 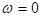дает время движения, 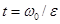, которое подставим в зависи­мость угла поворота от времени (22),

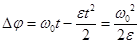
(сравните это с (22)). Подставляя сюда найденное выше 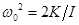, получаем

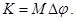
Отметим, что использование соотношения (61) с учетом того, что кинетическая энергия была полностью затрачена на работу сил торможения ( 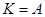), позво­ляет сразу написать полученный результат.

Наконец, угол поворота 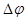связан с числом сделанных оборотов из­вест­ным соотношением (23) 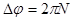, поэтому

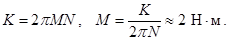
10. Однородный тонкий стержень массой 150г может вращаться вокруг вертикальной оси, проходящей через его середину. Летящий горизонтально со скоростью 10м/с, перпендикулярной стержню, пластилиновый шарик попадает в конец стержня и прилипает к нему. Найти скорость прилипшего шарика.

Решение:

Вертикальная проекция вектора суммарного момента внешних сил (ре­акции опоры и тяжести), действующих на систему тел «шарик-стержень», равна нулю, поэтому (см. (48`)) вертикальная проекция вектора момента импульса системы сохраняется. Сам вектор момента импульса определим относительно точки, совпадающей с центром стержня, чтобы (для упрощения описания) этот вектор тоже был направлен вертикально. Момент импульса шарика до удара (см. (45))

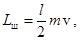
где 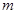– масса шарика, 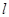– длина стержня, 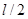– плечо импульса шарика, 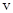– его скорость до удара. Стержень до удара покоился, поэтому его момент им­пульса был равен нулю, и момент импульса системы «шарик-стержень» до удара 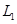равен :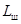

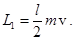
В результате удара стержень с прилипшим шариком будет вращаться. Момент импульса системы после удара (см. (49))

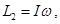
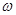– угловая скорость вращения стержня с шариком. Момент инерции системы 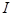складывается (см. (51)) из момента инерции стержня (56) и момента инерции шарика, который будем считать материальной точкой (52),

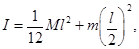
где 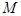– масса стержня. Сохранение момента импульса

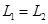
определяет угловую скорость вращения системы после удара

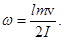
Линейная скорость прилипшего шарика 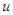связана с угловой скоростью 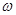соот­ношением (18)

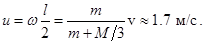
11. С наклонной плоскости скатывается два цилиндра 1) сплошной дере­вянный и 2) полый металлический. Внешние размеры и массы их одинаковы. Какой цилиндр скатывается быстрее?

Решение:

Согласно закону сохранения механической энергии потенциальная энер­гия цилиндра переходит в кинетическую, которая равна сумме энергий посту­пательного и вращательного движений (60):

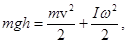
где 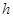– высота наклонной плоскости, 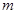– масса цилиндра, 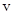– скорость его оси, 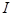– момент инерции цилиндра. Скорость 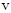оси цилиндра равна по величине скорости движения поверхности цилиндра относительно его оси, которая, в свою очередь, равна 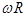(18),

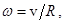
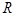– радиус цилиндра. Подставляя это в закон сохранения энергии, получаем

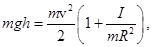
то есть,

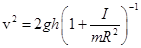
Два цилиндра в условии задачи имеют разные моменты инерции: сплошного цилиндра (57)

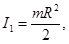
полого цилиндра, трубы (55)

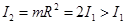
(массы и радиусы у них одинаковы по условию задачи). Поэтому скорость сплошного деревянного цилиндра больше скорости полого металлического,

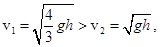
а так как они проходят одинаковые пути, время скатывания меньше,

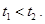
Деревянный цилиндр скатывается быстрее.