Производные основных элементарных функций 1 страница

1.	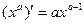1.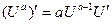
2.	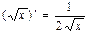2.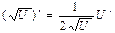
3.	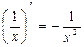3.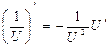
4.	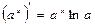4.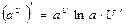
5.	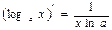5.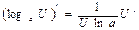
6.	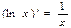6.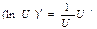
7.	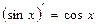7.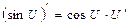
8.	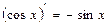8.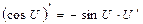
9.	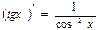9.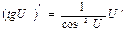
10.	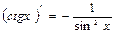10.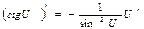
11.	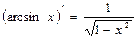11.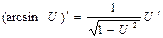
12.	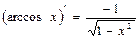12.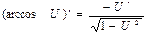
13.	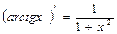13.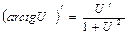
14.	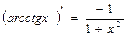14.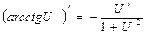

Задачи 11-20

Найти производные заданных функций:

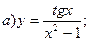
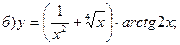
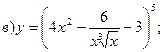
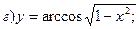
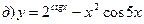
При вычислении производных нужно пользоваться приведенной выше таблицей производных.

Решение.

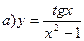
Воспользуемся формулами:

,

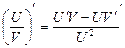где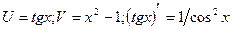

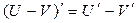
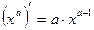
Тогда

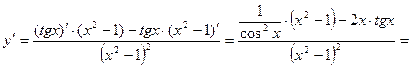
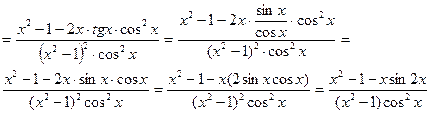
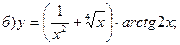
Воспользуемся формулами:

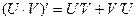
где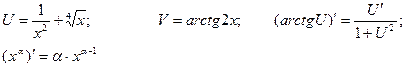

Тогда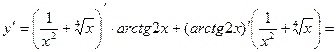

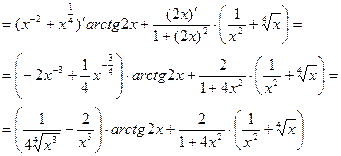
в)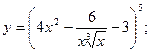

Данную функцию можно записать в виде степенной функции:

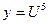, где

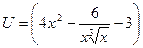
И, следовательно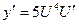

Заметим, что

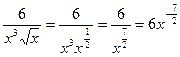
Значит,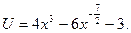

Тогда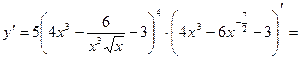

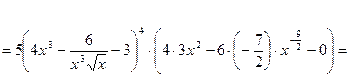
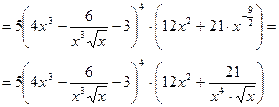
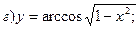
Данную функцию можно записать как: 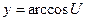, где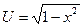

Тогда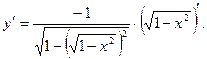

Для отыскания последней производной применим формулу:

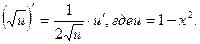
Значит,

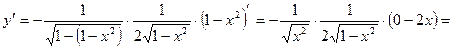
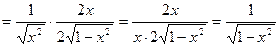
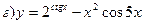
Воспользуемся формулами:

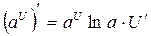
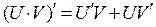
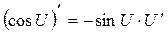
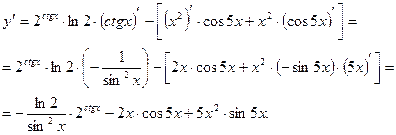
Задачи 21 -30

Исследовать средствами дифференциального исчисления функцию 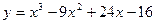и построить ее график.

Решение. Исследование будем проводить по следующей схеме:

1. Область определения функции.

В нашем примере это множество всех действительных чисел, то есть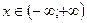

2. Четность и нечетность функции:

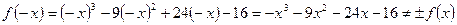Видим, что 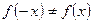и 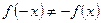, значит, функция

свойствами четности или нечетности не обладает.

Делаем вывод, что график функции не будет симметричен ни относительно оси , ни относи­тельно начала координат.

3.Периодичность функции.

Данная функция не является периодической, как многочлен.

4.Непрерывность функции.

На всей области определения данная функция является непре­рывной как многочлен.

5.Поведение функции на концах области определения.

Концами области определения являются «-∞» и « 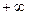», так как .

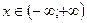Найдем пределы функции при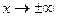

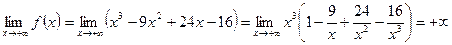
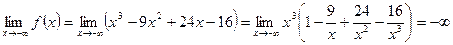
Таким образом, знак бесконечности определяется знаком старшего члена 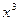. Это означает, что слева график функции уходит неограни­ченно вниз, а справа - неограниченно вверх

6. Интервалы монотонности и точки экстремумов.

Найдем точки «подозрительные» на экстремум. Согласно необхо­димого условия экстремума: в точках

экстремума производная равна нулю или не существует.

Находим производную: 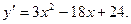. Она существует при лю­бых х. Решим уравнение :

; ;

; .

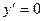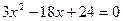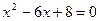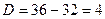
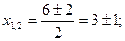
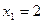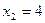Тогда можно записать: .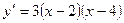

Точки х=2 и х=4 являются критическими. Они делят область оп­ределения на интервалы монотонности функции (интервалы возрас­тания и убывания). Изобразим их на числовой оси (рис.6).

Это интер­валы (-∞; 2);(2;4);(4;+∞).

	+	-	+

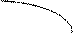Рис.6

Поведение функции на каждом интервале определяется знаком производной 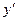: если 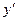<0, то функция убывает, если 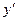>0, то функ­ция 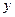возрастает.

Для определения знака производной на каждом интервале доста­точно взять любое значение х из этого интервала и подставить в про­изводную 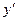= 3(х-2)(х-4).

а) На интервале (-∞; 2), возьмем любое х , например х=0, и под­ставим в производную 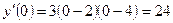.Получили 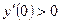, следовательно функция возрастает на интервале (-∞; 2).

б) На интервале (2;4) возьмем х=3, подставим в выражение для , получим 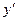(3)=3(3-2)(3-4)<0, следовательно, на интервале(2;4) функ­ция убывает.

в) На интервале (4;+∞) возьмем х=5,видим, что 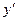(5)= 3(5-2)(5-4)>0, следовательно, на интервале (4;+∞) функция возрастает.

Знаки производной 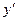проставлены на рис. 6 около каждого ин­тервала.

Замечаем, что при переходе через точку х=2 производная меняет знак, с (+) на (-) . Это означает, что в точке х=2 функция имеет мак­симум (на основании достаточного условия существования экстрему­ма). Найдем значение у при х=2:

.

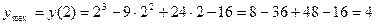Значит, точка максимума (2; 4).

При переходе через точку х=4 производная меняет знак с (-) на (+). Это означает, что при х=4 функция имеет минимум:

.

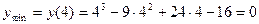Точка минимума (4;0).

7. Интервалы выпуклости, вогнутости и точки перегиба. Это исследование проводится с помощью второй производной

Найдем точки, подозрительные на перегиб, используя необходи­мое условие перегиба: в точках перегиба вторая производная либо равна нулю, либо не существует.

Так как 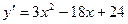, то 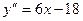существует при любых х. Приравняем вторую производную к нулю и найдем корни уравнения

6х -18=0. Отсюда х=3 - точка, подозрительная на перегиб.

Точка х=3 делит область определения (-∞; +∞) на интервалы: (-∞;3) и (3;+∞) (рис.7).

	-	+
		x

Рис. 7

Определим знаки второй производной на этих интервалах.

Если на интервале 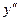>0, то график вогнутый, если 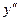<0, то гра­фик выпуклый (на основании достаточного условия выпуклости и вогнутости).

а) На интервале (-∞;3) возьмем, например, х=1, подставим во вторую производную у"=6(х-3) , получим 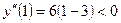, значит, при 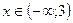график функции выпуклый.

б) На интервале (3;+∞) берем, например, х=5, подставим в 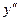,получим 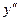(5) = 6(5-3)>0, значит, при х€(3;+∞) график функции вогнутый.

Знаки 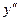проставлены на рис. 7 около каждого интервала.

Так как при переходе через точку х=3 вторая производная у" ме­няет знак, то график меняет выпуклость на вогнутость, то есть при х=3 график функции имеет перегиб.

.

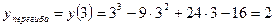Точка перегиба (3;2).

8.Точки пересечения графика с осями координат. С осью Оу: полагаем х=0 и, подставляя это значение в данную функцию у, находим у =-16; получим точку (0;-16). С осью Ох: полагаем у=0, находим х из уравнения

х³-9х²+24х-16=0 . (*)

Кубическое уравнение имеет хотя бы один действительный ко­рень, попробуем найти его подбором.

Корни уравнения являются делителями свободного члена 16. Следовательно, попробуем подставлять в уравнение (*) числа ±1; ±2; ±4; ±8; ±16.

При х=1: получаем 1-9+24-16=0, следовательно, х₁=1 является корнем уравнения (*). Тогда многочлен х³-9х²+24х-16 делится на (х-1) без остатка.

После деления в частном получится многочлен второй степени:

_ х³-9х²+24х-16 | х-1 .

х³-х² |х²-8х+16

_-8х²+24х-16

-8х²+8х

_16х-16

16х-16

Каждое слагаемое частного получается делением старшего члена делимого на старший член делителя:х³:х = х² (х² записываем в частное); умножаем (х-1) на х² и вычитаем из делимого. С остатком поступаем аналогично: -8х²:х = -8х (записываем в частное), умножаем (х-1) на (-8х) и вычитаем из остатка и т.д.

Итак, х³-9х²+24х-16 = (х-1)(х²-8х+16). Для отыскания остальных корней х₂ и х₃ решим уравнение х²-8х+16 =0, откуда получим .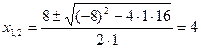

Окончательно: х³-9х²+24х-16 = (х-1)(х-4)².

Уравнение (*) принимает вид: (х-1)(х-4)(х-4)=0, откуда х,=1; х₂=4; х₃=4.

Таким образом, график функции пересекает ось ОХ в точках (1;0) и (4;0).

9. Дополнительные точки. Для более точного построения графика можно найти несколько дополнительных точек. Например, найдем у при х=5:

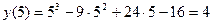. Получим точку К(5;4).

Выпишем результаты исследования функции у = х³-9х²+24х-16.

1. Область определения (-∞; +∞).

2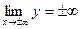

3. Функция возрастает при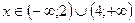

Функция убывает при .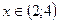

4.Точка max А (2;4), точка min В (4;0).

5. При 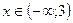- график выпуклый,

при 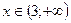- график вогнутый.

6.Точка перегиба С(3;2)

7.Точки пересечения с осями координат:(1;0), (4;0),(0;-16).

8.Дополнительная точка К (5;4).

Строим график функции (рис.8). Прежде всего построим все ха­рактерные точки, точки пересечения с осями, точки экстремумов, точку перегиба и дополнительные точки.

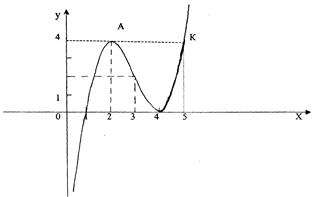
Рис.8

В силу непрерывности функции соединим все построенные точки плавной кривой, продолжив график влево и вправо согласно поведе­нию функции на концах области определения.

Задачи 31-40

Вычислить приближенное значение 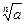, заменяя приращение функции 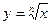дифференциалом, если n = 6,

а =60.

Решение: Нужно вычислить приближенно .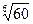

Приращение функции в точке : .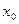

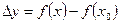Дифференциал функции в точке : .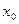

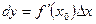При малых 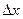: 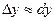или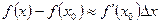

Отсюда получаем общую формулу для приближенных вычисле­ний: 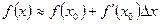, где .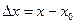

В нашей задач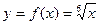е , где .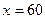

Найдем производную функции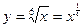

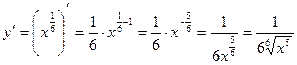
Приближенное равенство для функции 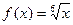будет иметь вид:

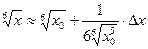
Здесь 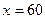, в качестве 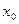выберем число 64, оно ближайшее 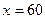, из которого точно извлекается корень шестой степени: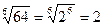

Следовательно, 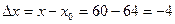. Подстав­ляя в последнюю приближенную формулу 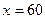, , 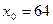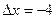най­дем нужный результат:

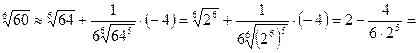
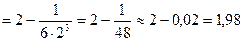
Ответ: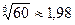

Задачи 61-70 относятся к теме "Функции нескольких переменных". Для решения этих задач необходимо познакомиться со следующими вопросами названной темы:

1. Определение функции двух переменных, область определения функции, геометрическое изображение функции двух переменных.

2. Определение частных производных первого порядка для функции двух переменных, их вычисление.

3. Полный дифференциал функции двух переменных.

4. Производные высших порядков для функции двух переменных.

5. Определение локальных экстремумов для функции двух переменных.

6. Необходимое и достаточное условия экстремума для функции двух переменных.

7. Правило исследования на экстремум для функции двух переменных.

Задачи 41-50

Найти полный дифференциал функции двух переменных

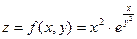
Решение.Полный дифференциал функции двух переменных на­ходим по формуле: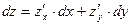

где 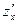; 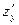--частные производные данной функции z.

Частные производные находим по обычным формулам дифферен­цирования для функции одной переменной, причем 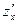находим, счи­тая «у» постоянной величиной; аналогично при отыскании 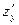счита­ем «х» постоянным:

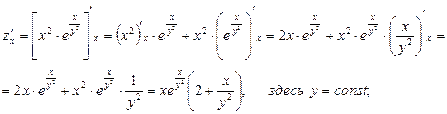
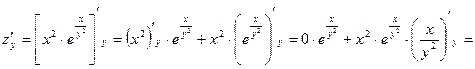
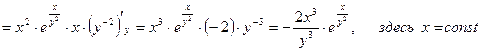
Отсюда полный дифференциал функции:

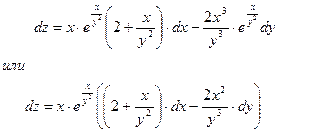
Задачи 51-60 и 61-70 относятся к теме «Интегральное исчисле­ние». Ознакомьтесь с основными вопросами этой темы:

1. Понятие первообразной и неопределенного интеграла.

2. Основные свойства неопределенного интеграла.

3. Таблица интегралов.

4. Основные методы интегрирования: непосредственное интегри­рование, интегрирование подстановкой, интегрирование по частям.

5. Интегрирование некоторых рациональных дробей.

6. Понятие определенного интеграла и его основные свойства.

7. Формула Ньютона-Лейбница для вычисления определенного интеграла.

8. Замена переменной и интегрирование по частям в определен­ном интеграле.

9. Применение определенного интеграла к вычислению площадей плоских фигур.

Интегрирование есть операция, обратная дифференцированию. ∫f(x)dx = F(x)+C, где F(х)-первообразная для подынтегральной функции f(x), то есть 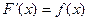, а С - произвольная постоянная. При интегрировании часто используют свойства неопределенного инте­грала:

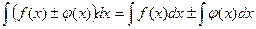
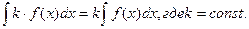
Идея интегрирования заключается в том, чтобы свести данный интеграл к одному из табличных интегралов. Поэтому, приступая к решению задач, ознакомьтесь с таблицей интегралов.

1.	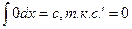1.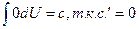
2.	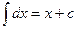2.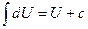
3.	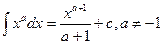3.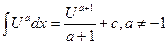
4.	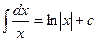4.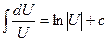
5.	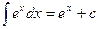5.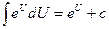
6.	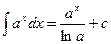6.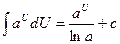
7.	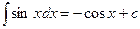7.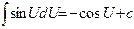
8.	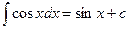8.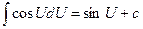
9.	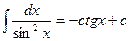9.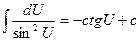
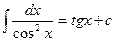10.	10.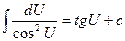
11.	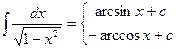11.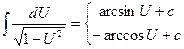
12.	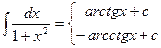12.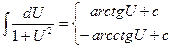
13.	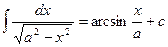13.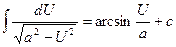
14.	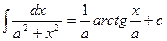14.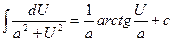
15.	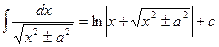15.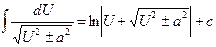
16.	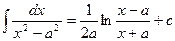16.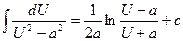