Математическое ожидание

Основная характеристика случайной величины – математическое ожидание, которое иногда называют средним значением. Среднее значение случайной величины есть некоторое число, являющееся как бы ее представителем, и заменяющее ее при грубо ориентировочных расчетах.

Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений.

· для дискретных случайных величин

М[X]= 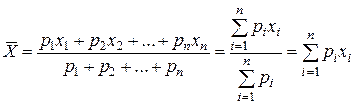; (I.4)

· для непрерывных случайных величин:

M[X]= 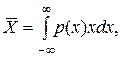(I.4)

где ;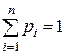

n – число интервалов наблюдения;

p(x) – плотность распределения случайной величины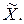

Математическое ожидание случайной величины тесным образом связано со средним арифметическим: при большом числе опытов среднее арифметическое наблюдаемых значений случайной величины приближается (сходится по вероятности) к ее математическому ожиданию. Тогда оценить величину математического ожидания случайной величины по выборке из N испытаний можно по формуле

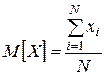, (I.5)

где N – число наблюдений случайной величины.

Математическое ожидание характеризует центр распределения.