Формулы показателей анализа ряда динамики
| Показатели | Способ расчета | |
| базисный | цепной  | |
| Абсолютный прирост | 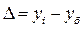 | 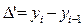 |
| Темп роста | 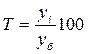 | 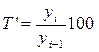 |
| Темп прироста | 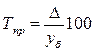 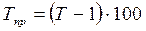 или или 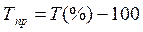 | 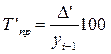 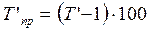 или или 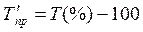 |
| Абсолютное содержание 1% прироста | 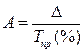 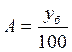 | 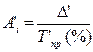 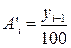 |
Условные обозначения: уi - уровень текущего периода; уi-1- уровень периода, предшествующего текущему; уб - базисный уровень (первый в ряду динамики).
В оценке динамики явлений большое значение имеют расчеты средних аналитических показателей, которые являются обобщающей характеристикой уровней, их абсолютной скорости и интенсивности изменения.
Методы расчета среднего уровня ряда динамики зависят от его вида и способов получения статистических данных.
В интервальном ряду динамики с равностоящими во времени уровнями расчет среднего уровня ( 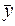 ) производится по формуле средней арифметической простой:
) производится по формуле средней арифметической простой:
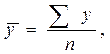
где n – количество хронологических дат.
Если интервальный ряд динамики имеет не равноотстоящие уровни, то средний уровень вычисляется по формуле:
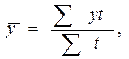
где t – количество периодов времени, в течение которых уровень не изменяется.
В моментных рядах динамики существует следующие варианты расчета среднего уровня:
1) дан ряд с равными интервалами времени между датами:
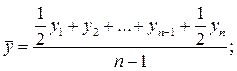
2) дан ряд с разными интервалами времени между датами и неизвестным характером изменений уровней между датами:
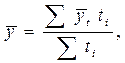
где 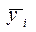 - средний уровень явления между двумя соседними датами.
- средний уровень явления между двумя соседними датами.
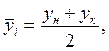
где 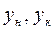 - начальный и конечный уровни на і-м интервале;
- начальный и конечный уровни на і-м интервале; 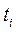 - длительность интервала времени между двумя соседними датами.
- длительность интервала времени между двумя соседними датами.
3) дан ряд с неравными интервалами времени между датами, но с исчер-пывающими данными об изменении явления между теми же датами:
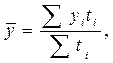
где yi – размер явления, который оставался неизменным в течение ti интервала времени.
Средний абсолютный прирост определяется по формуле:
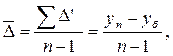
где 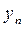 - конечный уровень ряда.
- конечный уровень ряда.
Средний темп роста рассчитывается по средней геометрической:
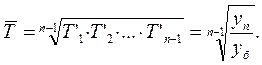
Средний темп прироста вычисляется так:
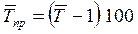 или
или 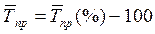
Среднее абсолютное содержание 1% прироста рассчитывается по формуле:
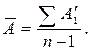
Одной из причин неверного отражения динамики явления слу-жит несопоставимость уровней ряда. Устранение несопоставимости уровней динамических рядов достигается использованием специальных приемов.
Смыкание рядов динамики применяется в случае несопоставимости уровней по территории, по кругу охватываемых объектов, по методике расчета показателей и др. Смыкание осуществляется двумя методами.
1. Использование коэффициентов пересчета. За год, когда возникла несопоставимость уровней, рассчитывается коэффициент, показывающий во сколько раз один уровень больше или меньше другого. Умножая на полученный коэффициент уровни ряда до изменения, приводят их к виду, сопоставимому с последующими уровнями.
2. Замена абсолютных уровней относительными, выраженными в базисных темпах роста. При этом уровень ряда за год, общий для сравниваемых рядов, принимается за 100%. Остальные уровни пересчитываются по отношению к этой базе сравнения, и получается новый ряд динамики, состоящий из относительных показателей.
При изучении рядов динамики возникает необходимость получения сравнительных характеристик направления и интенсивности роста одновременно развивающихся во времени явлений. Это достигается путем приведения рядов динамики к общему основанию. В этом случае данные о величине изучаемого показателя за год, принятый за базисный, принимают в каждом ряду за 100%, а уровни остальных лет относят к нему, получая базисные темпы роста.
Для оценки роста показателей сравниваемых параллельных рядов динамики за один и тот же период времени рассчитывают коэффициент опережения.
Его исчисляют как отношение базисных темпов роста (или средних годовых темпов роста) за одинаковые отрезки времени по двум динамическим рядам: 
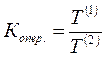 или
или 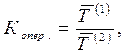
где 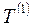 ,
, 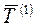 - соответственно базисные и средние годовые темпы роста одного ряда динамики;
- соответственно базисные и средние годовые темпы роста одного ряда динамики; 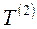 ,
, 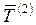 - соответственно базисные и средние годовые темпы роста второго ряда динамики.
- соответственно базисные и средние годовые темпы роста второго ряда динамики.
При этом в качестве первого ряда динамики берется тот ряд, темпы роста для которого выше.
Для характеристики скорости изменения уровней одного и того же ряда динамики за отдельные периоды времени определяют коэффициент ускорения (замедления).По аналогии с коэффициентом опережения он рассчитывается на основании базисных или средних годовых темпов роста:
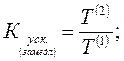
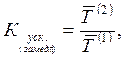
где 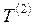 ,
, 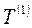 - базисные темпы роста уровней ряда динамики соответственно за второй и первый периоды одного и того же ряда динамики;
- базисные темпы роста уровней ряда динамики соответственно за второй и первый периоды одного и того же ряда динамики; 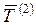 ,
, 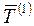 - средние годовые темпы роста соответственно за второй и первый периоды одного и того же ряда динамики
- средние годовые темпы роста соответственно за второй и первый периоды одного и того же ряда динамики
Тесты
