Влияние параметров системы на ее устойчивость. Исследование САР построением областей устойчивости (D-разбиения)

Пусть имеется характеристическое уравнение замкнутой системы

; .

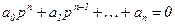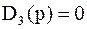Для определения того, в каком диапазоне могут меняться параметры a₁…a_n при устойчивой работе системы, был разработан и усовершенствован (1940 г. А.А. Соколов, 1948 г. Ю. И. Неймарк) метод выделения областей устойчивости.

Пусть имеется 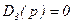– годограф Михайлова на границе устойчивости. Если система находится на границе устойчивости, то годограф Михайлова D(jv) проходит через начало координат, что может быть отображено уравнением:

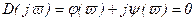, (6.45)

Выделим в уравнении (6.45) нужные параметры и начертим границу при v=0¸¥. Эта граница называется D-разбиением и представляет собой отображение границы устойчивости в плоскости корней в плоскости параметров системы.

Рисунок 6.26 D-разбиение

Чтобы система была устойчива, необходимо, чтобы все корни характеристического уравнения замкнутой системы были «левыми».

Коэффициенты характеристического уравнения зависят от постоянных времени

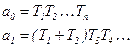
и т.д.

Для выяснения характера влияния параметров на устойчивость переносят границу устойчивости из плоскости корней в плоскость параметров. Это делают из условия D_з(jv)=0. В этом уравнении выделяют параметры и строят в плоскости параметров границу устойчивости (кривую D-разбиения).

Граница устойчивости выделяется штриховкой по правилу Неймарка. При движении по мнимой оси от w=-¥ до w=+¥ штрихуется левая сторона, оставляя область корней с отрицательной вещественной частью слева.

Имеем: 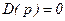- характеристическое уравнение замкнутой системы. Необходимо найти уравнение границы устойчивости, т.е. 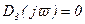при -¥<v<¥. Зададим, какие параметры будем исследовать, например A и B. Выделяем из уравнения D_з(jv) A и B и записываем

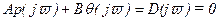и .

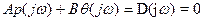D-разбиение для одного комплексного параметра.

1)Записываем 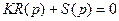, т.е. из полинома D(p) выносят параметр K, а S(p) – полином, не содержащий параметр K.

2)Далее 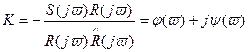- разделяем на вещественную и мнимую части.

3)Строим зависимость K(v), задаваясь различными значениями v. Получим границу областей устойчивости.

4) Выделяем области устойчивости штриховкой по Неймарку, для этого:

а) отмечаем направление движения v от -¥ к +¥;

б) заштриховываем левую часть кривой по отношению к движению.

Вся плоскость разбивается на три зоны (I, II и III) (рисунок 6.27). Часть плоскости, в сторону которой направлены штрихи (I зона) отображает левую полуплоскость корней и поэтому имеет наибольшее количество левых корней и является областью наибольшей устойчивости.

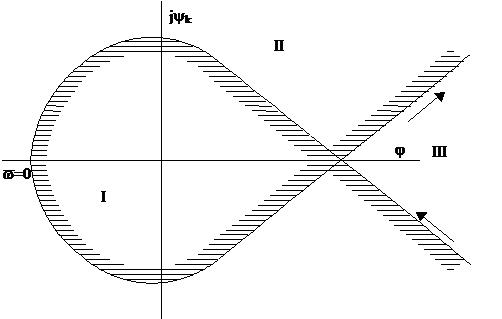
Рисунок 6.27 Граница областей устойчивости.

Переходя из I во II область, т.е. переходя кривую D-разбиения из заштрихованной части в не заштрихованную, теряется один отрицательный и приобретается один положительный корень (корень переходит в правую полуплоскость).

Запас устойчивости уменьшается в III области, где теряется два отрицательных корня.

Итак, область I (рисунок 6.27) имеет наибольший запас устойчивости. Проверяем устойчивость в точке 0. Так как параметр K - вещественный, то находим те значения K, которые находятся в I области на вещественной оси. При этих значениях САР будет обладать наибольшим запасом устойчивости.

Пример. Характеристическое уравнение замкнутой системы:

,

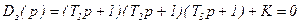T₁=0,5 с, T₂=0,1 с, T₃=1 с.

Найдем значение K, соответствующее наибольшей устойчивости.

1) ;

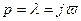2) ,

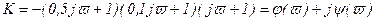где ;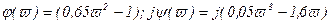

3)строим D-разбиение.

Таблица 6.2

v	0	1	2	3	5
φ(v)	-1	-0,35	1,6	4,85	15,85
ψ(v)	0	-1,55	2,8	-3,45	-1,75

4)так как параметр k-вещественный, то вещественные значения k=j(v) и лежащие на отрезке AB, т.е. от –1 до 19.8 соответствуют устойчивой работе САР.

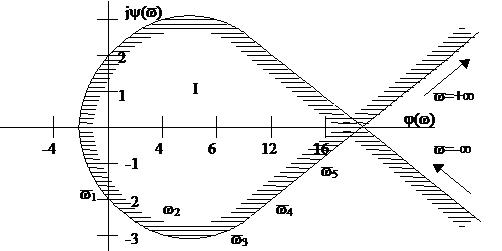
Рисунок 6.28 К примеру определения наибольшей устойчивости замкнутой системы

Часто бывает, что областей с различными областями устойчивости меньше степени характеристического уравнения, а значит и числа корней характеристического уравнения. В таком случае область наибольшей устойчивости дают только запас устойчивости, но не отвечает на вопрос, устойчива ли система, при этом необходимо после выбора параметров исследовать устойчивость другими методами.

Чаще всего это делают при значении параметра равном нулю, т.е. в начале координат кривой D-разбиения.

В нашем характеристическом уравнении положим k=0.

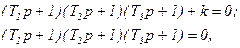
и найдем корни, приравнивающие к нулю все сомножители

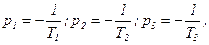т.е. I-я область соответствует устойчивой работе САУ при изменении k от –1 до 19,8, т.е. от 0 до 19,8.

Для определения абсолютного числа отрицательных корней для какого-нибудь частного значения исследуемого параметра надо решить характеристическое уравнение и найти число интересующих нас корней. Обычно величина параметра берется равной нулю (начало координат плоскости параметра). При этом характеристическое уравнение упрощается. В дальнейшем мы определяем число корней во всех зонах с помощью штриховки на кривой D-разбиения.

Выбираем область наибольшей устойчивости и сравниваем количество отрицательных корней с показателем степени n характеристического уравнения. Если количество отрицательных корней равно n, то система устойчива.