Устойчивость системы автоматического управления, математическое определение устойчивости

Система находится в состоянии равновесия, если при отсутствии воздействия на систему возмущающих факторов ошибка регулирования (разность между заданным и фактическим состоянием системы) стремится к нулю. Под устойчивостью понимается способность динамической системы возвращаться в равновесное состояние после окончания действия возмущения, нарушившего это равновесие. Неустойчивая система после воздействия возмущения удаляется от равновесного состояния или начинает совершать вокруг него колебания с нарастающей амплитудой.

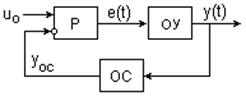
Возникновение неустойчивых (расходящихся) колебаний в системе можно проследить на примере следящей системы с обратной связью. Допустим, что в установившемся состоянии равновесия при опорном сигнале u_o на регуляторе Р выходное состояние объекта управления ОУ равно y_уст. Это состояние поддерживается сигналом рассогласования е_уст, который формируется в регуляторе Р по разности опорного сигнала и сигнала обратной связи у_ос-уст, т.е. е_уст = u_o-у_ос-уст. В первый момент включения системы в силу инерционности обратной связи у_ос = 0, а, следовательно, e(t) >> е_уст, что вызывает нарастание выходной величины y(t), которая будет стремиться к y(t) >> у_уст по крайней мере, до тех пор, пока сигнал обратной связи не начнет уменьшать значение e(t). Однако значительно возросшая величина y(t) через ОС передается на вход регулятора системы и может настолько существенно уменьшить значение e(t), что это может привести к последующему снижению величины выходного сигнала до значений y(t) << у_уст, т.е. к возникновению колебательного процесса относительно равновесного состояния. При неблагоприятном соотношении параметров системы колебательный процесс может быть незатухающим и даже расходящимся. Пример такого процесса в концертной акустике хорошо известен – свист из динамиков, если коэффициент обратной связи от динамиков на микрофоны на определенных частотах становится положительным.

Устойчивость линейной системы определяется не характером возмущения, а структурой самой системы. Говорят, что система устойчива "в малом", если определен факт наличия устойчивости, но не определены ее границы. Система устойчива "в большом", когда определены границы устойчивости и то, что реальные отклонения не выходят за эти границы. Соответственно, и задача исследования систем на устойчивость может быть поставлена двояко:

1) устойчива ли система при заданном значении ее параметров;

2) в каких диапазонах можно изменять параметры системы, не нарушая ее устойчивости.

Вторая задача исследования имеет место при наладке и эксплуатации систем автоматического управления.

В соответствии с классическим методом решение дифференциального уравнения для системы ищется в виде:

y(t) = у_св(t) + у_вын(t).

Здесь у_св(t) – свободная составляющая, общее решение однородного дифференциального уравнения с нулевой правой частью:

a₀y⁽ⁿ⁾ + a₁y^(n-1) + ... + a_n-1y’ + a_ny = 0,

т.е. когда все внешние воздействия сняты, и состояние системы определяются лишь собственной структурой.

Функция у_вын(t) представляет собой частное решение неоднородного дифференциального уравнения, под которым понимается уравнение с ненулевой правой частью. Физически это означает, что к системе приложено внешнее воздействие u(t). Поэтому вторая составляющая общего решения называется вынужденной. Она определяет вынужденный установившийся режим работы системы при наличии на входе определенного воздействия u(t) или f(t) после окончания переходного процесса.

Применительно к сигналам в САУ частное решение для вынужденной составляющей обычно имеет простой вид, не влияющий на устойчивость. Вопрос устойчивости сводится к выяснению устойчивости свободного движения системы и требует анализа характера решения уравнения свободного движения, составленного относительно отклонения выходной величины y(t)от установившегося состояния.

Как известно, передаточная функция любой линейной динамической системы может быть приведена к виду:

W(p) = K(p)/H(p) =

= [b₀p^m+b₁p^m-1+…+b_m-1p+b_m] / [a₀pⁿ+a₁p^n-1+…+ a_n-1p+a_n],

где a и b - постоянные коэффициенты, которые представляют собой вещественные числа и выражаются через конкретные физические параметры элементов системы. Полином К(р) может не содержать членов с оператором р и представлять собой произведение коэффициентов передачи звеньев, образующих систему.

Важнейшим свойством выражения является условие n≥m, т. е. порядок полинома Н(р) знаменателя передаточной функции не ниже порядка полинома К(р) ее числителя. Это условие вытекает из физических свойств звеньев реальных динамических систем.

Из выражения передаточной функции системы можно получить дифференциальное уравнение системы в целом, как в разомкнутом, так и в замкнутом состоянии.