Измерение индуктивности проволочной катушки

Рассмотрим индуктивность, к которой приложено переменное напряжение .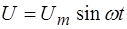

Ток I и напряжение U на индуктивности связаны соотношением:

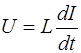. (8)

Если мы заменим в схеме на рис. 2 С₀ на L₀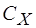, а на 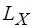, то, используя соотношение (8) и рассуждения, аналогичные тем, которые мы провели выше, получим

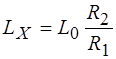. (9)

Таким образом, мостовая схема, к которой приложено переменное напряжение, может быть использована для определения электрической ёмкости и индуктивности.

Обсудим особенности измерения индуктивности мостовым методом и вопрос о точности таких измерений.

Катушка индуктивности представляет собой в простейшем случае тонкую медную проволоку, плотно намотанную в один слой на цилиндрический каркас из непроводящего материала.

При подаче на индуктивность L переменного синусоидального напряжения U сдвиг фазы между напряжением и током составляет 90° (рис. 3). Амплитуда напряжения на индуктивности и тока через нее связаны между собой соотношением

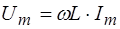. (10)

Коэффициент, связывающий между собой ток и напряжение в (10), определяет эффективное сопротивление индуктивности в цепи переменного тока

_.

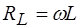Очевидно, что это сопротивление растет с повышением частоты w.

Реальная проволочная катушка индуктивности обладает некоторым активным сопротивлением. Поэтому эквивалентная схема катушки индуктивности представляет собой последовательно включенные индуктивность L и активное сопротивление R (рис. 3а).

Рис. 3

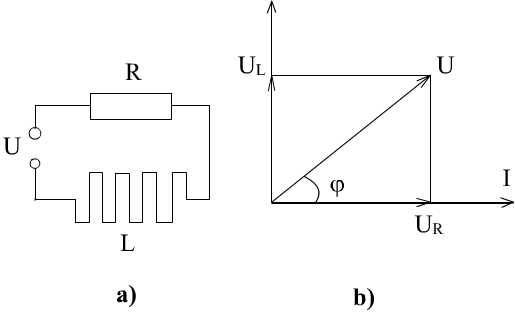Напряжение на индуктивности опережает по фазе на 90° напряжение на сопротивлении, что отражено на векторной диаграмме напряжений (рис. 3b). Результирующее напряжение 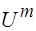определяется как результат векторного сложения 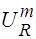и .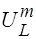

Амплитуды напряжения 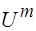и тока 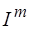, сдвиг фазы j связаны между собой соотношениями

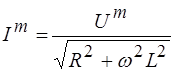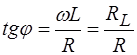, . (11)

При получении соотношения (9) для 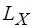мы пренебрегли влиянием сопротивления R. Выясним условия, при которых влияние R мало, и оценим точность определения 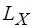с помощью формулы (9) при этих условиях. Воспользуемся соотношением (11), представив его в следующем виде:

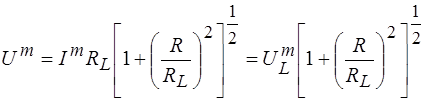. (12)

Для того чтобы влияние R на результаты измерения было мало, должно быть выполнено соотношение

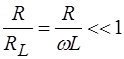. (13)

Рассмотрим катушку индуктивности из медной проволоки (рис. 3). Длина катушки 1, диаметр катушки D. Обозначим диаметр проволоки через d, массу проволоки m, длину проволоки A, ее сопротивление R. Можно показать, что индуктивность такой катушки при условии l>>D определяется следующим выражением

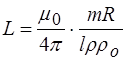, (14)

где 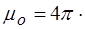10^-7 Гн/м – магнитная постоянная;

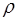=1,6×10^-8 Ом×м – удельное сопротивление меди;

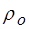=8,9 г/см³ – удельный вес меди.

Из формулы (14) видно, что отношение 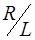пропорционально отношению 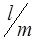. Таким образом, для катушек индуктивности, изготовленных из проволоки одинакового диаметра, отношение 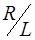будет оставаться постоянным, т.к. масса проволоки пропорциональна длине l катушки.

Возьмем катушку из медной проволоки с конкретными параметрами:

m=50 г, l=6 см, D=2 см, d=0,3 мм.

Тогда число витков 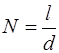=200.

Длина проволоки 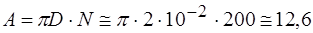м.

Сопротивление 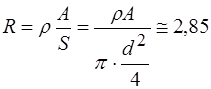Ом.

Индуктивность 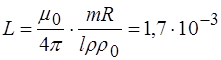Гн.

Индуктивное сопротивление 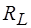при частоте

f=100 Гц 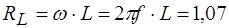Ом,

f=10 кГц 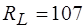Ом.

Таким образом, при частоте f=10 кГц соотношение (13) выполняется, а именно,

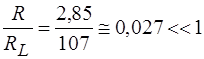. (15)

Отметим, что при изменении диаметра проволоки d отношение 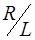, полученное из формулы (14), будет меняться, но по порядку величины будет оставаться тем же для реально используемых катушек индуктивности. Поэтому соотношение (15) является справедливым для реальных катушек.

В мостовой схеме (рис. 2) сравниваются напряжения на индуктивностях L₀ и L_X. При условии (15) R<<R_L, а при частоте f=10 кГц расчет результирующего напряжения по формуле (12) дает значение

,

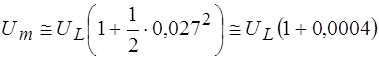т.е. отличие 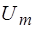от 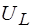составляет ~0,04%.

Следовательно, погрешность измерения L_X, вносимая активным сопротивлением катушки, при частоте f=10 кГц, составляет ~0,04%. На самом деле реальная погрешность будет еще меньше, поскольку образцовая катушка также обладает некоторым активным сопротивлением (см. (9)).

В заключение приведем некоторые рекомендации для практической оценки погрешности измерений индуктивности.

1. При использовании моста переменного тока увеличение частоты задающего генератора уменьшает погрешность измерения индуктивности.

2. Если образцовая и измеряемая катушки имеют одинаковую форму (сравнимые отношения 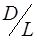) и намотаны одинаковым проводом, то погрешность определения L_X за cчет активного сопротивления провода будет существенно меньше полученной из формулы (12).

3. Если образцовая и измеряемые катушки имеют разную форму, намотаны проводом разного сечения, сделаны из разного материала, то в этом случае ни при каком положении подвижного контакта 3 реохорда (рис. 2) не удастся добиться нулевого показания милливольтметра. Это связано с разностью фаз напряжений в точках 3 и С. Отношение минимального напряжения милливольтметра к напряжению на индуктивности L₀ (или L_X) может служить мерой погрешности измерения L_X.