Погрешность результата измерения
Архангельский государственный технический университет
Аналитические методы определения
Погрешности измерения
Методические указания к выполнению практических работ
Архангельск 2008
Рассмотрены и рекомендованы к изданию методической комиссией химико-технологического факультета Архангельского государственного технического университета
Составитель
Т.М. Владимирова, доц., канд. техн. наук
Рецензент
УДК
Владимирова, Т.М. Аналитические методы определения погрешности результата измерения: методические указания к выполнению практических работ / Т.М. Владимирова. – Архангельск: Изд-во Арханг. гос. техн. ун-та, 2008. – с.
Подготовлены кафедрой стандартизации, метрологии и сертификации.
В методических указаниях приведены порядок и методика аналитического определения характеристик погрешности результатов измерений в различных режимах измерения, а также формирования алгоритмов обработки многократных измерений, изложены основные теоретические положения изучаемых разделов.
Настоящие методические указания предназначены для студентов специальности 200501.65 – «Метрология и метрологическое обеспечение», изучающих дисциплину «Общая теория измерений», а также «Метрология, стандартизация и сертификация».
Ил. . Табл. . Библиогр. назв.
Ó Архангельский государственный
технический университет, 2008
Ó Т.М. Владимирова, 2008
ВВЕДЕНИЕ
Измерение вероятностных характеристик случайных процессов начинается с разработки методов и средств измерения характеристик измерительных сигналов.
Область распространения статистических методов исследования и обработки сигналов-носителей информации безгранична. Связь, навигация, управление процессами, движением и т.п., диагностика, как техническая, так и медицинская, исследования среды и многие другие области немыслимы без знания и использования свойств сигналов, описываемых их вероятностными характеристиками.
Потребность в изучении свойств случайных процессов привела к развитию соответствующих методов и средств измерений, появилась потребность в обеспечении необходимого метрологического уровня измерений вероятностных характеристик. Потребность в формировании основ теории измерения обусловлена широким использованием измерительных методов и средств в практических исследованиях свойств случайных процессов и большим количеством разработанных алгоритмов, устройств и методов описания и изучения их возможностей.
Средства измерений с развитием вычислительной техники превращаются в измерительно-вычислительные системы или комплексы, характеризующиеся общим нормированием метрологических характеристик.
Опираясь на то, что измерение – это экспериментальное определение числовых характеристик физических величин или объектов, можно сформулировать две проблемы, без решения которых нельзя развивать теорию и практику измерений. При этом теория измерений опирается на теорию вероятностей, теорию случайных функций и математическую статистику.
Первая проблема сводится к выбору такого пути развития теории измерений, который учитывал бы положения теории классической метрологии, а вторая – необходимостью установления связи между определением вероятностных характеристик с результатами измерений. Результатом совместного решения этих проблем стал вывод о том, что особенностью измерений вероятностных характеристик является введение дополнительных ограничений по достижимой точности, обусловленные конечностью объема выборочных данных о результате измерения. В результате, формирование алгоритмов для определения методических погрешностей проводится на основе принятых в классической метрологии методов.
Настоящие методические указания предназначены для студентов специальности 200501.65 – «Метрология и метрологическое обеспечение», выполняющих практические работы по дисциплине «Общая теория измерений».
Целью практических работ является развитие и закрепление навыков аналитического определения характеристик погрешности результатов измерений в различных режимах измерения, а также формирования алгоритмов обработки многократных измерений.
Погрешность результата измерения
Вся количественная информация о неизвестном истинном значении измеряемой физической величины заключается в результате измерения. В процессе измерения можно получить результаты измерений, как хорошего качества, так и плохого, в зависимости от множества факторов. Это и условия измерений, и качество измерительной техники, и тип алгоритма обработки результатов измерений, и много других причин.
Так как результат измерений это случайная величина, то характеристиками качества измерения являются вероятностные характеристики этой случайной величины: плотность распределения (полная характеристика) или числовые и функциональные характеристики (математическое ожидание, дисперсия, ковариационная функция). Сами по себе характеристики случайного результата измерения без сопоставления с истинным значением измеряемой физической величиной не дают полной картины о качестве результата измерения. С практической точки зрения показатели качества нужно выбирать таким образом, чтобы они характеризовали меру отличия результата измерений от истинного значения измеряемой физической величины. Поэтому такой интегральной характеристикой качества результата измерения стала погрешность – «погрешность результата измерения» или более коротко «погрешность измерения».
Погрешность измерения – это алгебраическая разность между результатом измерения и истинным значением измеряемой физической величины. Обозначим погрешность Е(t). Ее выражение по определению (для детерминированной физической величины) имеет следующий вид
E(t) = Y(t) – x(t),
где Y(t) = 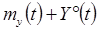 – результат измерения как случайная функция;
– результат измерения как случайная функция;
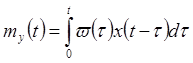 – математическое ожидание результата измерения;
– математическое ожидание результата измерения;
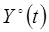 – центрированная случайная составляющая результата измерения как случайная функция, обусловленная наличием в процессе измерения случайных возмущающих факторов.
– центрированная случайная составляющая результата измерения как случайная функция, обусловленная наличием в процессе измерения случайных возмущающих факторов.
В основу расчета характеристик погрешности результата измерения положена структурная схема формирования погрешности, приведенная на рис. 1.1.
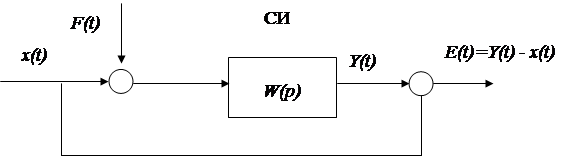 |
Рис. 1.1 Структурная схема формирования погрешности:
x(t) – детерминированная измеряемая величина как функция времени; F(t) = mf(t)+F(t) – аддитивное случайное возмущение, накладывающееся на измеряемую величину; mf(t) – математическое ожидание случайной функции F(t); F(t) = F(t) – mf(t) – центрированная стационарная случайная функция со спектральной плотностью Sf(w); W(p) = k×Wo(p) –
передаточная функция СИ; k = 1/q = 1+Dk – коэффициент чувствительности СИ; Dk = – Dq – отклонение коэффициента чувствительности от идеального значения, равного единице; q – размер единицы величины, воспроизводимой СИ; Dq = q – 1 – погрешность единицы величины, воспроизводимой СИ; Wo(p) – нормированная передаточная функция СИ 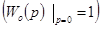 .
.
Измеряемая физическая величина представляется следующей математической моделью
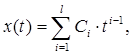
где Сi, 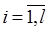 - постоянные коэффициенты.
- постоянные коэффициенты.
Математическое ожидание аддитивного возмущения, действующего на измеряемую величину, представляется также аналогичной математической моделью
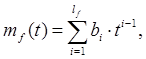
где bi, 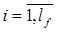 - постоянные коэффициенты.
- постоянные коэффициенты.
Спектральная плотность центрированной стационарной составляющей F(t) представляется следующими выражениями
1. 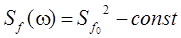
2. 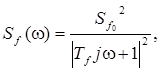
где Tf, Sfo – постоянные величины.
Характеристики среды оказывают двоякое влияние на результат измерения: во-первых, через искажение истинного значения измеряемой физической величины, а во-вторых, через измерение параметров, а следовательно и свойств средства измерения. Такой двоякий характер влияния среды на результат измерения послужил основанием для выделения двух основных составляющих погрешности.
2. Расчет характеристик погрешности результата измерения
Основными составляющими погрешности результата измерения, которые необходимо определить в работе являются: мультипликативная погрешность, аддитивная погрешность и суммарная погрешность. В области преобразования Лапласа выражения для этих составляющих и суммарной погрешности имеет следующий вид
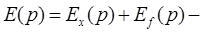 уравнение суммарной погрешности;
уравнение суммарной погрешности;
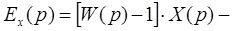 уравнение мультипликативной погрешности;
уравнение мультипликативной погрешности;
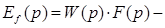 уравнение аддитивной погрешности.
уравнение аддитивной погрешности.
Используя обратное преобразование Лапласа, получим
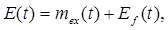 (2.1)
(2.1)
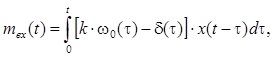 (2.2)
(2.2)
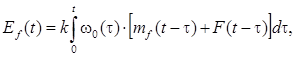 (2.3)
(2.3)
где w0(t) – нормированная весовая функция СИ,
d(t) – единичная d – функция.
Запишем выражение (2.1) в следующем виде
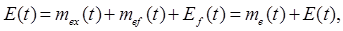 (2.4)
(2.4)
где 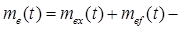 систематическая погрешность результата измерения,
систематическая погрешность результата измерения,
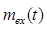 – мультипликативная составляющая погрешности,
– мультипликативная составляющая погрешности,
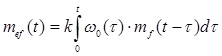 – аддитивная составляющая систематической погрешности (2.5),
– аддитивная составляющая систематической погрешности (2.5),
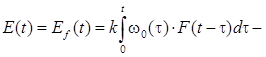 центрированная случайная погрешность результата измерения, обусловленная случайной составляющей аддитивного возмущения, накладывающегося на измеряемую величину Х(t) на входе СИ.
центрированная случайная погрешность результата измерения, обусловленная случайной составляющей аддитивного возмущения, накладывающегося на измеряемую величину Х(t) на входе СИ.
