Производные основных элементарных функций 2 страница

Примечание:Формулы интегрирования сохраняют свой вид при подстановке вместо независимой переменной любой дифференцируемой функции от нее, т.е. если

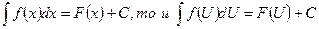
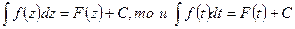
Tаким образом, применение основной таблицы сразу расширяется.

Например

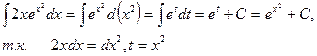
Задачи 51 – 60

Найти неопределенные интегралы. Результаты проверить диффе­ренцированием.

Интегралы б), в), г), д) в ваших контрольных работах берутся методом замены переменной (подстановкой).

При этом вводится новая переменная t = φ(x), которая является функцией от х. Если новая переменная введена удачно, то в результа­те замены получаем табличные интегралы.

Некоторые рекомендации по введению новой переменной смот­рите ниже в примерах.

Напомним формулу для нахождения дифференциала функции одной переменной:

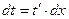или

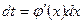
Пример 1.

Если под знаком интеграла содержится показательная функция, то за новую переменную t удобно принимать показатель степени, ес­ли под интегралом присутствует производная этого показателя с точ­ностью до постоянного множителя.

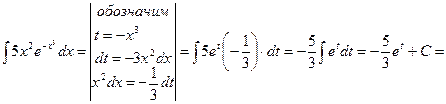
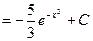
В конце возвращаемся к первоначальной переменной, подставив вместо t выражение (-x³).

Проверка. Если интеграл взят правильно, то производная от по­лученного результата равна подынтегральной функции:

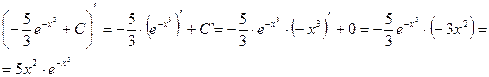
что и требовалось доказать.

Пример 2.

Если под интегралом содержится логарифмическая функция, то удобно принять ее за новую переменную, если под знаком интеграла присутствует производная этой функции (с точностью до постоянно­го множителя).

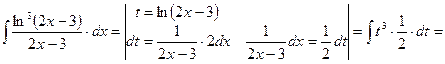
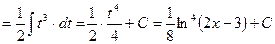
Проверка:

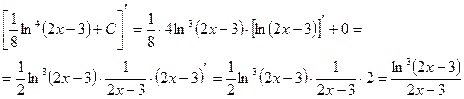
Пример 3.

Часто удобно обозначать за новую переменную знаменатель дро­би подынтегральной функции.

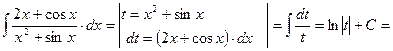
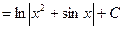
Проверка:

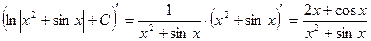
Пример 4.

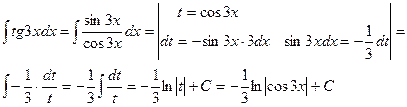
Проверка:

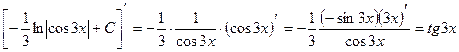
Пример 5.

Часто за новую переменную удобно взять подкоренное выраже­ние, если под интегралом присутствует также его производная с точ­ностью до постоянного множителя.

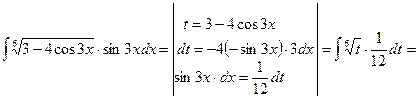
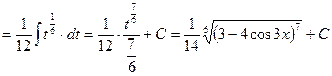
Проверка:

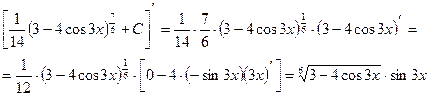
Пример 6.

Подстановка выбирается аналогично предыдущему примеру.

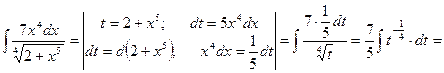
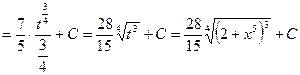
Примечание.Сделайте самостоятельную проверку в примере 6-14

Пример 7.

Новая переменная иногда выбирается из следующих соображе­ний: в знаменателе стоит разность постоянной и квадрата некоторой функции. Эту функцию мы принимаем за новую переменную, если в числителе присутствует ее производная (с точностью до постоянного множителя).

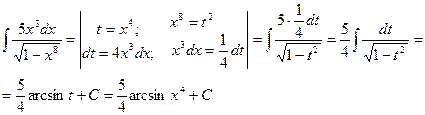
Пример 8.

Подстановка выбирается аналогично предыдущему примеру.

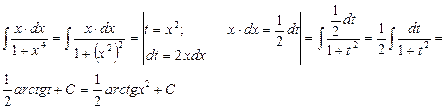
Пример 9.

За новую переменную иногда выбирают функцию, стоящую в основании степени, если подынтегральное выражение содержит про­изводную этой функции с точностью до постоянного множителя.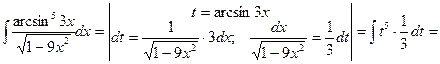

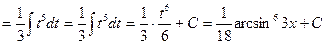
Пример 10.

Подстановка выбирается аналогично предыдущему примеру.

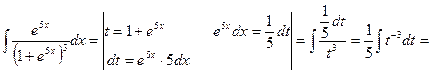
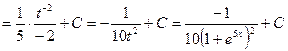
Интеграл из пункта е) вашей контрольной работы берется мето­дом интегрирования «по частям». Этим методом интегрируются не­которые произведения, например, произведения степенной функции на логарифмическую или на показательную, или на тригонометриче­скую, или на обратные тригонометрические функции и др.

Интегрирование «по частям» производится по формуле

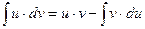
Чтобы воспользоваться этой формулой, следует один множитель в подынтегральном выражении обозначить за « 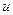», а оставшийся множитель вместе с 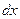принять за « ».

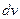Для того, чтобы интеграл в правой части был проще данного ин­теграла, надо правильно выбрать « 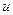» и « ».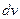

В интегралах, берущихся по частям, обычно логарифмическую и обратные тригонометрические функции принимают за «u». Если по­дынтегральная функция содержит произведение степенной функции на показательную или тригонометрическую, то за «u» принимается степенная функция.

Пример 11.

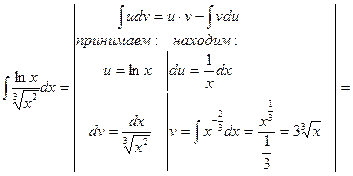
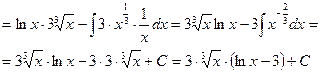
Пример 12.

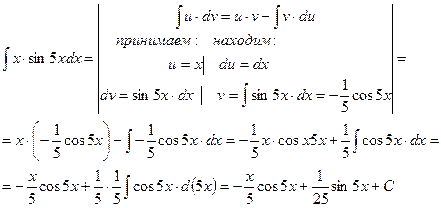
Пример 13.

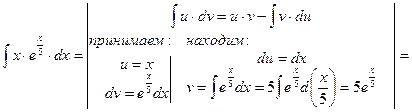
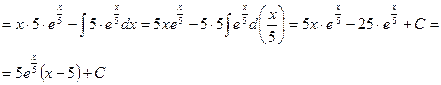
Пример 14.

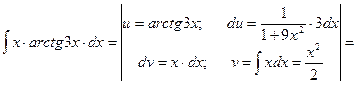
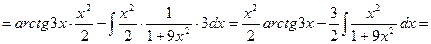
Чтобы взять последний интеграл, умножим и разделим числитель на 9, затем вчислителе прибавим иотнимем единицу, после чего ра­зобьем интеграл на два табличных:

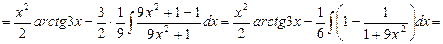
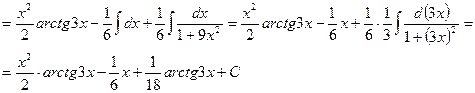
Обязательно сделайте проверку в примерах 6-14.

Задачи 61-70

В этих задачах используется определенный интеграл, который вычисляется по формуле Ньютона-Лейбница.

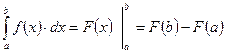
где F(x) - первообразная для f(x), то есть F'(x) = f(x);

a и b - пределы интегрирования, показывающие, как меняется переменная интегрирования х.

Обратите внимание на то, что определенный интеграл - это чис­ло в отличие от неопределенного интеграла, который является множеством функций. Формула Ньютона-Лейбница связывает опреде­ленный и неопределенный интегралы. Чтобы ею воспользоваться, следует взять сначала неопределенный интеграл (вернее, найти лишь одну первообразную, не прибавляя произвольной постоянной), а за­тем вычислить разность значений первообразной в верхнем и нижнем пределах интегрирования.

Например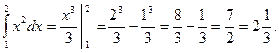

Задача. Вычислить площадь фигуры, ограниченной параболой 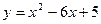и прямой 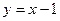. Сделать чертеж.

Решение. Построим параболу и прямую.

Для построения параболы найдем координаты ее вершины и точ­ки пересечения ее с осями координат.

Вершина параболы является точкой экстремума, поэтому для ее отыскания найдем производную и приравняем ее к нулю.

; ; ,

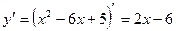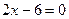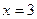Тогда .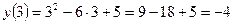

Итак, вершина параболы в точке .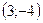

Точки пересечения параболы с осью Ох: 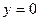, тогда

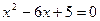, откуда 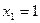; 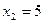, то есть точк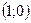и и .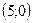

Точка пересечения с осью Оу: 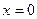, тогда 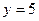; то есть точка .

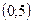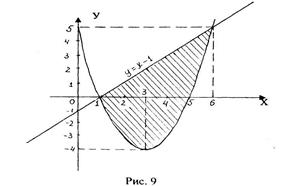
Строим параболу по найденным точкам, замечая, что ветви пара­болы направлены вверх (рис. 9).

Прямую у = х-1 строим по двум точкам: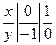

получены точки (0;-1) и (1 ;0). Заштрихуем плоскую фигуру, ограниченную параболой и пря­мой.

Найдем точки пересечения параболы и прямой, решив систему уравнений:

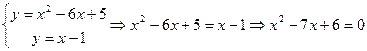
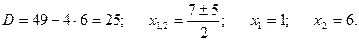
Для отыскания искомой площади воспользуемся формулой

,

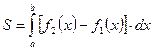где функции f₁(x) и f₂(x) ограничивают фигуру соответственно снизу и сверху, то есть f₂(х) ≥f₁ (х) при х Є [а;b].

В нашей задаче f₁(x) = x² -6x + 5;f₂(x) = x-l; x Є [l;6].

Поэтому

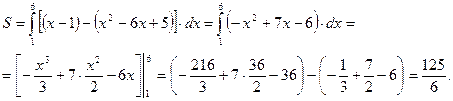
Ответ: Площадь искомой криволинейной трапеции:

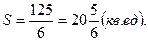
Задачи № 71-90

Названные задачи относятся к теме «Дифференциальные уравнения». По этой теме необходимо изучить следующие вопросы:

1. Какое уравнение называется дифференциальным? Как определяется порядок дифференциального уравнения?

Определение. Уравнение, связывающее независимую переменную 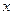, искомую функцию 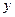и ее производные, называется дифференциальным.

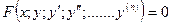или

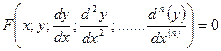
Порядок дифференциального уравнения определяется наличием наивысшей производной:

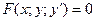- дифференциальное уравнение первого порядка

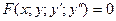- дифференциальное уравнение второго порядка

2. Что называется решением дифференциального уравнения? Общее и частные решения дифференциальных уравнений первого и второго порядка.

Определение. Решением дифференциального уравнения называется такая функция 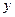, которая вместе с ее производными удовлетворяет этому уравнению (превращает его в тождество).

Общее решение имеет вид: .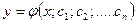

Решение, полученное из общего при конкретных значениях произвольных постоянных 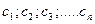называется частным.

Общее решение дифференциальных уравнений первого и второго порядка имеют соответственно вид:

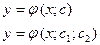
3. Задача Коши для дифференциального уравнения первого и второго порядков.

Задача отыскания частного решения дифференциального уравнения, удовлетворяющего начальным условиям:

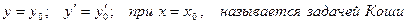
Дифференциальное уравнение первого порядка с разделяющимися переменными: 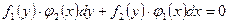. Нахождение их общего и частного решений.

4. Дифференциальные уравнения первого порядка с разделяющимися переменными 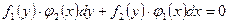сводится к уравнению с разделенными переменными 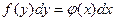, которое решается интегрированием обеих частей:

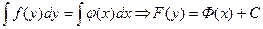
5. Линейное дифференциальное уравнение первого порядка: 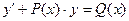Отыскание его общего и частного решений.

Линейные дифференциальные уравнения первого порядка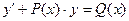

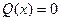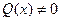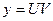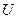при является уравнением с разделяющимися переменными. Если , то уравнение решается с помощью подстановки ,где и 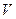неизвестные функции, зависимые от 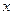. После ряда преобразований линейное уравнение сводится к двум дифференциальным уравнениям с разделяющимися переменными.

6. Линейные однородные и неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами, нахождение их общих и частных решений.

Задача. Найти общее решение дифференциального уравнения 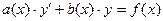и частное решение, удовлетворяющее начальному условию .

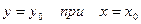Уравнения предлагаемого вида являются линейными, так как содержат искомую функцию « 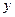» и ее производную « 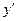» в первых степенях. Один из способов решения таких уравнений заключается в том, что функцию y(x) ищем в виде произведения двух дифференцируемых функций u(x) и v(x), одна из которых подбирается специальным образом, а другая находится из условия их удовлетворения исходному уравнению. С помощью этого приема решение линейного дифференциального уравнения первого порядка сводится к решению двух дифференциальных уравнений с разделяющимися переменными соответственно для функций u(x) и v(x).

Рассмотрим ряд примеров. Напомним, что производная равна отношению дифференциалов:

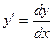
Пример 1.

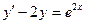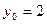; при .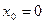

Ищем решение уравнения в виде 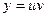. Найдем производную этого произведения: 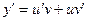. Подставим функцию y и ее производную 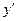в исходное уравнение:

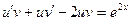
В левой части уравнения сгруппируем слагаемые, имеющие общий множитель « 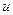», и вынесем его за скобку:

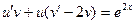
Подберем вспомогательную функцию « 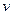» так, чтобы обратилось в нуль выражение, стоящее в круглых скобках:

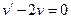(1)

Тогда уравнение примет вид:

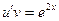(2)

Оба последних уравнения решаются разделением переменных.

Сначала находим частное решение первого из них, то есть функцию 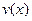, а затем, подставив ее во второе уравнение, найдем функцию .

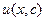1) 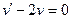; 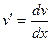2) ; ; ; ;

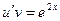
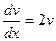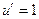
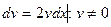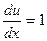
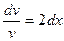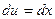
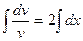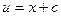
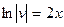
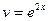
Замечание. Решая первое уравнение (для вспомогательной функции 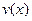), берем лишь его частное решение, соответствующее 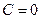. При решении второго уравнения для функции 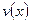находим общее решение уравнения.

Так как 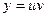, то 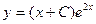- общее решение уравнения.

Для нахождения частного решения обратимся к начальному условию: 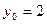при 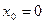. Подставим эти значения в найденное общее решение дифференциального уравнения:

,

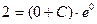так как 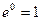, то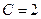

Подставим найденное значение С в общее решение дифференциального уравнения, получим его частное решение:

.

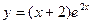Ответ: 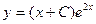- общее решение дифференциального уравнения;

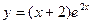- частное решение дифференциального уравнения.

Пример 2. ;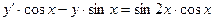

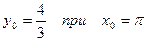
Ищем решение в виде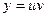

Найдем производную: .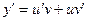

Подставим в исходное уравнение 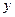и :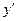

;

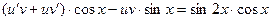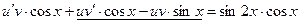
Сгруппируем подчеркнутые слагаемые, вынеся за скобку общий множитель u:

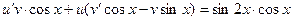
Подберем вспомогательную функцию 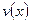из условия:

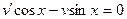(1)

Тогда уравнение примет вид:

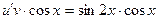(2)

Решаем поочередно два последних уравнения, причем для первого из них берем лишь частное решение 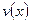, соответствующее .

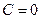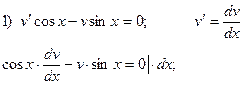
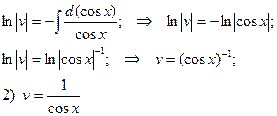
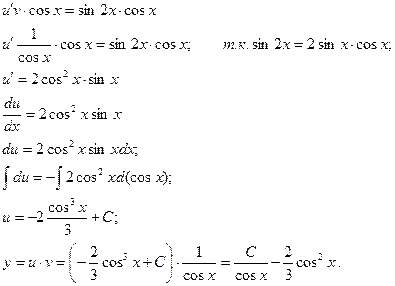
Таким образом, 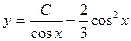- общее решение данного дифференциального уравнения.

Для нахождения частного решения воспользуемся начальными условиями: 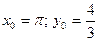, подставив их в найденное общее решение:

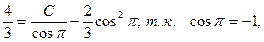
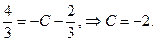
Подставим 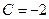, в общее решение уравнения:

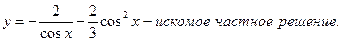
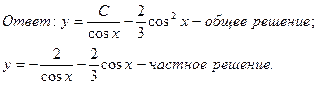
Пример 3.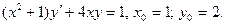

Ищем решение в виде 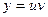, тогда .

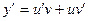Подставим 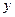и 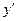в данное уравнение:

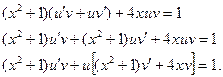
Потребуем, чтобы 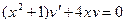(1) , тогда 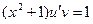(2)

Решим последовательно оба уравнения, причем для первого из них берем лишь частное решение при .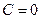

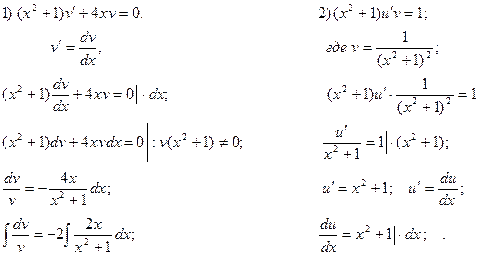
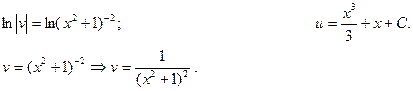
Так как 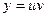, то

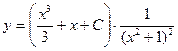- это общее решение исходного дифференциального уравнения.

Для нахождения частного решения обратимся к начальным условиям 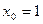; 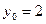и подставим их в найденное общее решение:

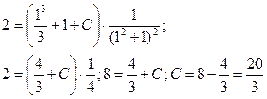
Искомое частное решение получим из общего, подставив в него найденное значение :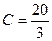

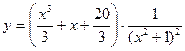
Ответ: 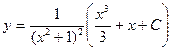- общее решение;

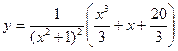- частное решение.

Замечание. Чтобы проверить правильность найденного решения (общего или частного), нужно подставить его в исходное уравнение и убедиться, что получится верное равенство (тождество).

Пример 4. Найти частное решение уравнения:

,

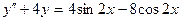удовлетворяющее начальным условиям .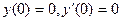

Решение. Общее решение 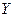данного уравнения равно сумме общего решения 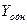однородного уравнения и какого-либо частного решения 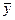данного уравнения, то есть