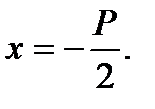Жазықтықтағы түзу теңдеулері.
Түзулердің теңдеулері
 |
 |
 |
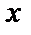 |
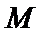 |
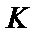 |
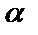 |
| 1-сурет |
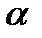 (0<
(0< 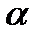 <
< 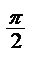 ) бұрыш жасасын. Түзу бойынан қандай да бір М(х,у) нүкте алайық. Түзудің Ох осімен жасаған
) бұрыш жасасын. Түзу бойынан қандай да бір М(х,у) нүкте алайық. Түзудің Ох осімен жасаған 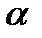 бұрышының тангенсін ВМК үшбұрышынан табамыз:
бұрышының тангенсін ВМК үшбұрышынан табамыз: 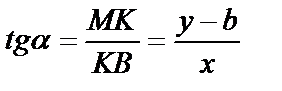 (1)
(1)
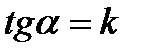 деп белгілеп, түзудің бұрыштық коэффициентідеп атау қабылданған. Сонымен:
деп белгілеп, түзудің бұрыштық коэффициентідеп атау қабылданған. Сонымен:
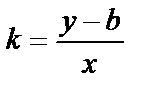 .
.
Осы қатынастан у-ті тапсақ:
y=kx+b (2)
Түзу бойында жатқан кез келген нүктенің координатасы (2) теңдеуді қанағаттандырады да түзуден тыс жатқан нүктелер бұл теңдеуді қанағаттандырмайды.
(2) теңдеу түзудің бұрыштық коэффициентімен берілген теңдеуі деп аталады.
Дербес жағдайларын қарастырайық.
1. Түзудің бұрыштық коэффициентімен берілген теңдеуіндегі b=0 болсын. Онда түзу теңдеуі y=kx түрге келеді де, түзу координат басынан өтеді (2-сурет)
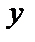 |
| x=a |
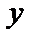 |
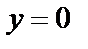 |
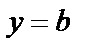 |
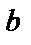 |
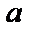 |
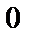 |
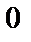 |
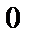 |
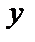 |
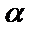 |
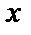 |
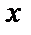 |
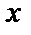 |
| 2-сурет 3-сурет 4-сурет |
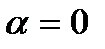 болса, онда
болса, онда 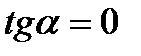 болады да, түзу теңдеуі y=b түрге келеді де, түзу Ох осіне параллель болады (3-сурет). Ал Ох осінің теңдеуі y=0 болады.
болады да, түзу теңдеуі y=b түрге келеді де, түзу Ох осіне параллель болады (3-сурет). Ал Ох осінің теңдеуі y=0 болады. 3. Егер 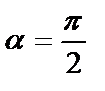 болса, онда
болса, онда 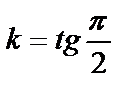 мәні болмайды, түзу Ох осіне перпендикуляр болады. Айталық түзу Ох осінен а тең кесінді қиып өтеді, сонда түзу теңдеуі х=а түрде болады (4-сурет). Ал Оу осінің теңдеуі х=0 болады.
мәні болмайды, түзу Ох осіне перпендикуляр болады. Айталық түзу Ох осінен а тең кесінді қиып өтеді, сонда түзу теңдеуі х=а түрде болады (4-сурет). Ал Оу осінің теңдеуі х=0 болады.
Мынадай теорема айтуға болады.
Теорема. Тік бұрышты координаталар жүйесінде кез келген түзу бірінші ретті теңдеумен беріледі
Ах+Ву+С=0 (3)
Және керісінше, (3) теңдеу (А, В, С коэффициенттердің бәрі бір мезгілде нолге тең болмаған кезде) тік бұрышты координаталар жүйесінде қандай да бір түзуді анықтайды.
(3) теңдеуді әдетте түзудің жалпы теңдеуі деп атайды.
Берілген бағыт және берілген нүкте арқылы өткен түзу теңдеуі.Көп жағдайда түзу теңдеуін оның бойында жатқан белгілі 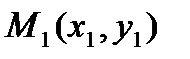 нүкте мен k бұрыштық коэффициенті арқылы жазу керек болады (5-сурет).
нүкте мен k бұрыштық коэффициенті арқылы жазу керек болады (5-сурет).
 |
 |
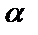 |
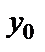 |
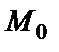 |
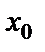 |
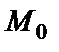 |
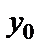 |
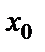 |
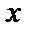 |
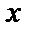 |
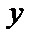 |
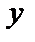 |
| 5-сурет 6-сурет |
Түзу теңдеуін (2) түрінде жазайық, y=kx+b, мұндағы b әзірше белгісіз. Түзу 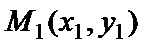 нүктесі арқылы өтетіндіктен, нүкте координатасы түзу теңдеуін қанағаттандыруы керек: y1=kx1+b.Осы теңдіктен белгісіз b табылады, b = y1 - kx1. Табылған мәнді теңдеудегі орнына қойып, берілген бағыт және берілген нүкте арқылы өткен түзу теңдеуін аламыз:
нүктесі арқылы өтетіндіктен, нүкте координатасы түзу теңдеуін қанағаттандыруы керек: y1=kx1+b.Осы теңдіктен белгісіз b табылады, b = y1 - kx1. Табылған мәнді теңдеудегі орнына қойып, берілген бағыт және берілген нүкте арқылы өткен түзу теңдеуін аламыз:
y =k(x – x1)+ y1 (4)
Егер (4) теңдеудегі k ерікті мән қабылдаса, онда теңдеу 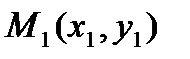 нүктесі арқылы өтетін түзулер шоғының теңдеуін анықтайды (6-сурет).
нүктесі арқылы өтетін түзулер шоғының теңдеуін анықтайды (6-сурет).
 |
 |
 |
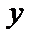 |
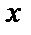 |
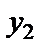 |
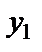 |
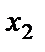 |
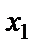 |
| 7-сурет |
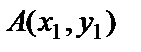 және
және 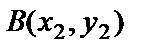 нүктелері берілсін. АВ түзуінің теңдеуін жазу үшін А нүктесі арқылы өткен түзулер шоғының теңдеуін жазамыз:
нүктелері берілсін. АВ түзуінің теңдеуін жазу үшін А нүктесі арқылы өткен түзулер шоғының теңдеуін жазамыз: y =k(x – x1)+ y1.
АВ түзуі 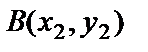 нүктесі арқылы өтетіндіктен, нүкте координатасы түзу теңдеуін қанағаттандыруы керек: y2 =k(x2 – x1)+ y1. Осы теңдіктен белгісіз k табылады,
нүктесі арқылы өтетіндіктен, нүкте координатасы түзу теңдеуін қанағаттандыруы керек: y2 =k(x2 – x1)+ y1. Осы теңдіктен белгісіз k табылады, 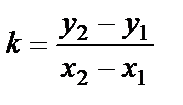 . Табылған мәнді теңдеудегі орнына қойып, берілген екі нүкте арқылы өткен түзу теңдеуін аламыз:
. Табылған мәнді теңдеудегі орнына қойып, берілген екі нүкте арқылы өткен түзу теңдеуін аламыз:
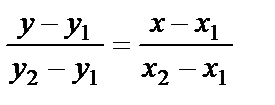 (5)
(5)
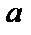 |
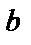 |
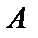 |
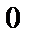 |
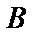 |
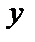 |
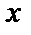 |
| 8-сурет |
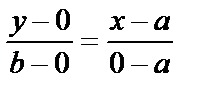
Енді ықшамдасақ, түзудің “кесіндідегі” теңдеуін аламыз:
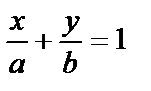 (6)
(6)
Екі түзу арасындағы бұрыш.Екі түзу берілсін: y=k1x+b1, y=k2x+b2. Мұндағы 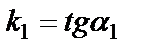 , , 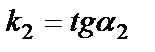 . Екі түзу арасындағы . Екі түзу арасындағы 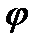 бұрышты табу керек (9-сурет). бұрышты табу керек (9-сурет). |
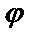 |
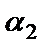 |
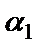 |
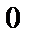 |
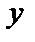 |
 |
| 9-сурет |
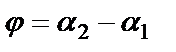 . Осыдан
. Осыдан 
немесе
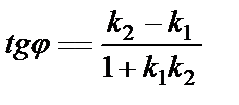 (7)
(7)
(7) формула берілген екі түзу арасындағы бұрышты анықтайды. Ал екінші бұрыш 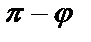 тең болады.
тең болады.
Екі түзудің параллелдік және перпендикулярлық шарты.Егер екі түзу параллель болса, онда 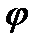 =0 болады да tg
=0 болады да tg 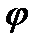 =0. Бұл жағдайда (7) формула мынадай түрге келеді: k2 – k1 = 0. Осыдан екі түзудің параллелдік шарты шығады:
=0. Бұл жағдайда (7) формула мынадай түрге келеді: k2 – k1 = 0. Осыдан екі түзудің параллелдік шарты шығады:
k2 = k1 , (8)
яғни екі түзудің бұрыштық коэффициенттері тең болса, ол түзулер параллель болады және керісінше.
Егер екі түзу перпендикуляр болса, онда 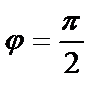 болады да,
болады да, 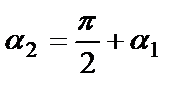 ,
, 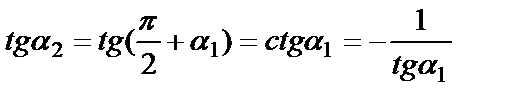 . Осыдан екі түзудің перпендикулярлық шарты шығады:
. Осыдан екі түзудің перпендикулярлық шарты шығады:
k2 = 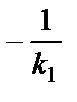 , (9)
, (9)
яғни екі түзудің бұрыштық коэффициенттері мәндері бойынша кері, таңбалары бойынша қарама-қарсы болса, ол түзулер перпендикуляр болады және керісінше.
10.Екінші ретті қисықтар:
1. Эллипс.Фокустар деп аталатын берілген екі нүктеден қашықтықтарыньң қосындысы әрқашанда тұрақты шама болатын жазықтықтағы нұктелердің геометриялык орындарын эллипс деп атайды (9-сызба). Анықтама бойынша F1M + F2M = 2a
нүктелер,
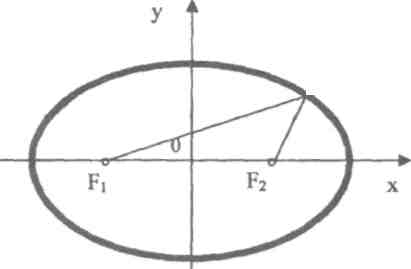 |
М{х, у) -эллипстің бойындағы кез келген жылжымалы нүкте,
2а-тұрақты шама
Егер F1F2= 2с десек,ондаF1(-C;0), F2(C;0).Сонда:
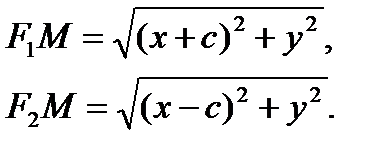
Енді осы мәндердіқойсақ:
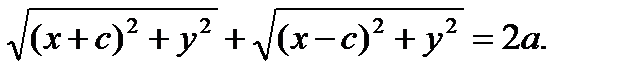
Немесе

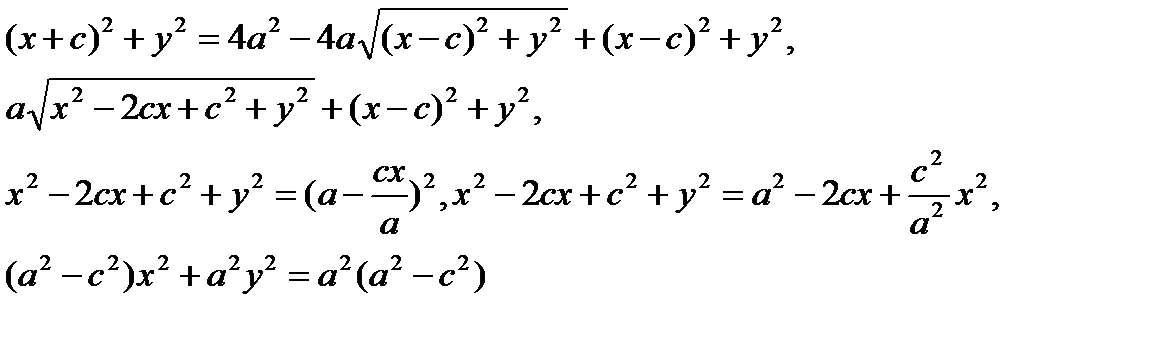
Егер а>с болса, ондаа2 —с2=b2 болады. Сондықтан эллипстің канондық теңдеуі деп аталатын теңдеуге келеміз:
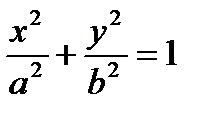
Мұндағы х пен у эллипстің кез келген жылжымалы нүктесінің координаттары, а -эллипстің үлкен жарты oci, b -онын кіші жарты oci.
Осьтер эллипске симметриялы, ал симметриялы осьтердің қиылысатын нуктесі эллипстің цeнтpi болады.
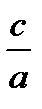 қатынасын эллипстің эсцентриситеті деп атайды және оны
қатынасын эллипстің эсцентриситеті деп атайды және оны 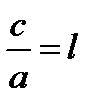 деп белгілейді. Сонымен 6ipгe а > с болғандьқтан l <1 немесе
деп белгілейді. Сонымен 6ipгe а > с болғандьқтан l <1 немесе 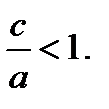
Эллипстің үлкен осіне перпендикуляр тузулердің ішінде 6ipтүзудің эллипстің кші осінен қашықтықты d әрқашанда а/l қатынасына тең тұрақты шама болса, онда мұндай тузудіэллипстің директрисасы деп атайды. Директрисалардың тендеу 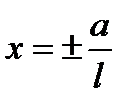 .Эллипс үшін l <1 болғандьқтан
.Эллипс үшін l <1 болғандьқтан 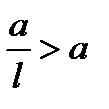 .
.
Сондықтан эллипстің дериктрисалары оның сыртында жатады.
Егер a=b болса, онда шеңбер эллипстің дерпбес жағдайы болады. Бұл жағдайда с=0, ендеше шеңбердің эксцентриситеті нөлге тең.
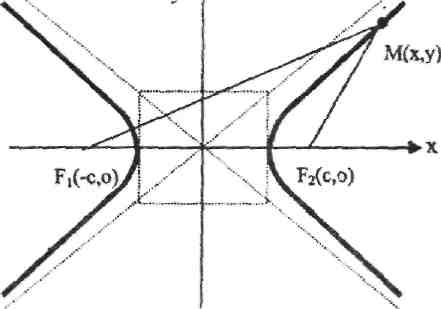
3. Гипербола.Фокустар деп аталатын берілген екі нүктеден
қашықтықтарының айырмасы әрқашанда тұрақты шама болатын
жазықтыктағы нүктелердің геометриялық орындарын гипербола деп атайды.
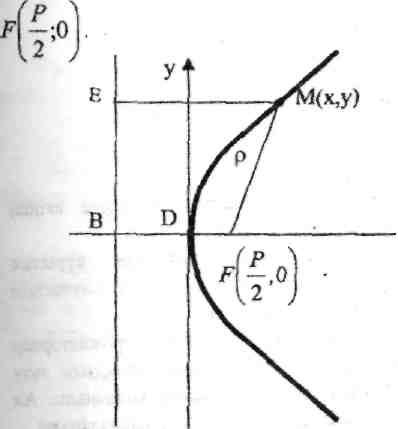
5. Парабола. Фокус деп аталатын
берілген нүктеден және
директриса деп аталатын берілген
түзуден ара қашықтықтары бірдей
болатын жазықтықтарды
нүктелерің геометриялык орындарын
парабола дейді Берілген F
нуктесінің координаталарын былай белгілейді
 |
| ► * |
Координаталардың бас нүктесінен Р/2 қашықтықтағы ординат осіне параллель берілген
тузуді параболаның директрисасы дейді.
М(х,у) - параболаның бойындағы кез келген жылжымалынүкте.
Анықтама бойынша
FM=ME
Екі нүктенің ара қашықтыгыньң формуласы бойынша
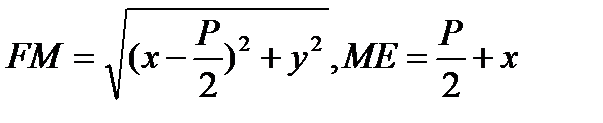
осы мәндерді апарып қойып, шыққан өрнекті түрлендірсек, параболаның канондық теңдеуі шығады:
у2=2рх
мұндагы р -берілген фокус пен директрисаның арасындағы қашықтық, х пен у - параболаның бойындағы кез келген жылжымалы нуктенің координатасы.
Параболаның эксцентриситеті: 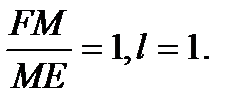
Параболаның директрисасының теңдеуі: