Суміжність

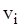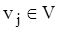Дві вершини і графа 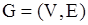називаються суміжними, якщо вони є граничними вершинами ребра 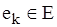. Відношення суміжності на безлічі вершин графа можна визначити, представивши кожне ребро як пари суміжних вершин, тобто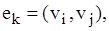 Для неорієнтованих графів такі пари неупорядковані, так що 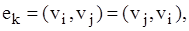а для орграфів — упорядковані, причому 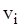і 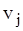, означають відповідно початкову і кінцеву вершини дуги 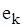. Петля при вершині 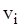в обох випадках представляється неупорядкованою парою 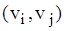. Ясно, що безліч вершин 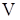разом з визначеним на ньому відношенням суміжності цілком визначає графа.

Граф можна представити також матрицею суміжності. Рядки і стовпці цієї матриці відповідають вершинам графа, а її 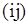елемент дорівнює числу кратних ребер, що зв'язують вершини 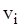і 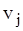(чи спрямованих від вершини 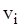до вершини 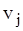для орграфа). Наприклад, для графів, приведених на мал. 3.2,а і 3.3,а, маємо відповідно наступні матриці суміжності:

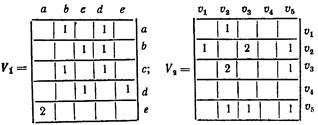
Матриця суміжності неорієнтованого графа завжди симетрична, а орграфа — у загальному випадку несиметрична. Неорієнтованим ребрам відповідають пари ненульових елементів, симетричних щодо головної діагоналі матриці, дугам — ненульові елементи матриці, а петлям — ненульові елементи головної діагоналі. У стовпцях і рядках, що відповідають ізольованим вершинам, всі елементи дорівнюють нулю. Елементи матриці простого графа рівні 0 чи 1, причому всі елементи головної діагоналі нульові.

Для зваженого графа, що не містить кратних ребер, можна узагальнити матрицю суміжності так, що кожен її ненульовий елемент дорівнює ваги відповідного чи ребра дуги. Назад, будь-яка квадратна матриця 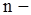го порядку може бути представлена орграфом з 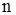вершинами, дуги якого з'єднують суміжні вершини і мають ваги, рівні відповідним елементам матриці. Якщо матриця симетрична, то вона може бути представлена неорієнтованим графом.