Визначник добутку матриць

Можна показати, що визначник добутку двох квадратних матриць А і В однакових порядків дорівнює n добутку їхніх визначників: 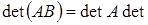. Для цього розглянемо матрицю порядку 2n

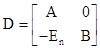
де E_n – одинична матриця.

Застосовуючи розкладання Лапласа по першим n рядкам визначника цієї матриці, маємо ½D½=½A½½B½. Представимо визначник ½D½ у виді:

½D½=	а (1),	а (2),	. . .	а (n)
-1		. . .		b (1)
	-1	. . .		b (2)
. . .	. . .	. . .	. . .	. . .
		. . .	-1	b (n)

де а ⁽¹⁾, а ⁽²⁾, . . ., а ⁽ⁿ⁾ - стовпці матриці A; b ₍₁₎, b ₍₂₎, . . ., b _(n) - рядки матриці В; 0 — нульова матриця n-го порядку.

Перетворимо визначник |D| до такого виду, щоб на місці елементів b_ij (i,j = 1,2, ..., п) були нулі. Для цього перший стовпець помножимо на елементи рядка b ₍₁₎ і додамо його до відповідних (п + 1, п +2, ..., 2п) стовпців. Аналогічно зробимо з другим, третім і т.д. до п-го включно стовпцями. У результаті одержимо:

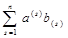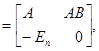½D½=	а (1),	а (2),	. . .	а (n)
-1
	-1
		. . .
			-1

де сума в правому верхньому куті замінена добутком А В в відповідності з (1.4).

На основі розкладання Лапласа по першим п рядкам знаходимо, що ½D½= ½АВ½. Таким чином, | АВ | = | А||В | чи det(AB)= detAdet, що і було потрібно довести.

Природним узагальненням цього результату є теорема Бене—Коші про визначник добутку АВ двох прямокутних матриць розміру (т ´ п) і (п ´ т):

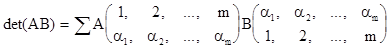
де сума означає, що складаються добутки всіляких мінорів m-го порядку матриці А, утворені т її стовпцями з номерами a₁, a₂, .... a_т, та мінори матриці В, утворені її рядками з тими ж номерами. В інших позначеннях цю теорему можна записати в такий спосіб:

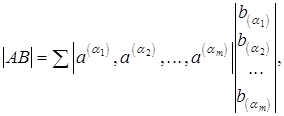
де a₁, a₂, .... a_т — усілякі сполучення з п номерів, розташовані в порядку їхнього проходження.

При т>п вважають | АВ | = 0, а при т = п маємо розглянутий вище окремий випадок добутку квадратних матриць.

Зі співвідношення 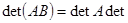випливає, що визначники можна множити за правилами множення матриць. Приклад:

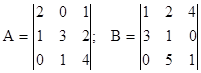
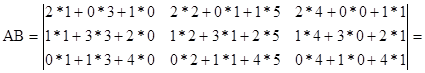
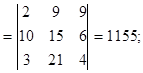
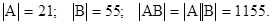
На закінчення відзначимо, що 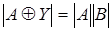| і 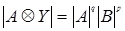, де q — порядок матриці В і р — порядок матриці А.

3. ГРАФИ.

3.1. ПОНЯТТЯ ГРАФА.