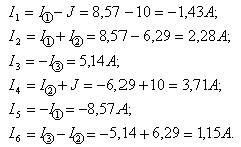Метод контурных токов
Определим количество независимых контуров схемы рисунок 7.2:
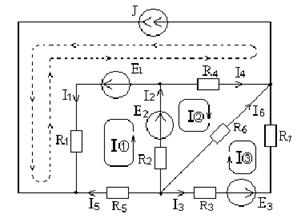
Рисунок 7.2
Количество независимых контуров определяем по формуле:
m = в–(у–1) = 6–(4–1)=3,
где в = 6 – количество ветвей схемы без учета ветви с источником тока;
у = 4 – количество узлов.
Система содержит 3 уравнения, т.к. в данной схеме 3 независимых контура.
Запишем систему контурных уравнений:
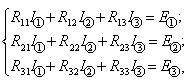 (7.2)
(7.2)
где 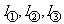 – контурные токи. Положительные направления контурных токов заданы произвольно и указаны на схеме;
– контурные токи. Положительные направления контурных токов заданы произвольно и указаны на схеме;
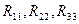 – собственные контурные сопротивления, равные сумме сопротивлений, входящих в данный контур (всегда положительны).
– собственные контурные сопротивления, равные сумме сопротивлений, входящих в данный контур (всегда положительны).
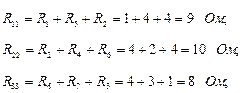
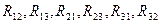 – общие (взаимные) контурные сопротивления, т.е. сопротивления ветвей общие для двух контуров. Они могут быть и положительными и отрицательными. Положительные – если контурные токи через общее сопротивление протекают в одном направлении; отрицательные – если в разных направлениях.
– общие (взаимные) контурные сопротивления, т.е. сопротивления ветвей общие для двух контуров. Они могут быть и положительными и отрицательными. Положительные – если контурные токи через общее сопротивление протекают в одном направлении; отрицательные – если в разных направлениях.
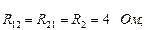
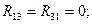
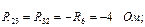
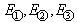 – контурные ЭДС. Контурные ЭДС равны алгебраической сумме ЭДС всех источников данного контура. При этом ЭДС, направление которых совпадает с направлением контурного тока, берем с положительным знаком, в противном случае – с отрицательным знаком. В контурных ЭДС необходимо учесть и действие источника тока. Для этого ток источника тока надо замкнуть по любым ветвям (на схеме рис.7.2 показано пунктиром) и определить падение напряжения от этого тока. Это падение напряжения необходимо прибавить к соответствующим контурным ЭДС или вычесть. Прибавляем, если для данного контура направление тока источника тока не совпадает с направлением контурного тока. Вычитаем, если ток источника тока совпадает с направлением контурного тока. Эти правила основаны на использовании теоремы компенсации для сопротивлений, через которые протекает замкнутый ток J.
– контурные ЭДС. Контурные ЭДС равны алгебраической сумме ЭДС всех источников данного контура. При этом ЭДС, направление которых совпадает с направлением контурного тока, берем с положительным знаком, в противном случае – с отрицательным знаком. В контурных ЭДС необходимо учесть и действие источника тока. Для этого ток источника тока надо замкнуть по любым ветвям (на схеме рис.7.2 показано пунктиром) и определить падение напряжения от этого тока. Это падение напряжения необходимо прибавить к соответствующим контурным ЭДС или вычесть. Прибавляем, если для данного контура направление тока источника тока не совпадает с направлением контурного тока. Вычитаем, если ток источника тока совпадает с направлением контурного тока. Эти правила основаны на использовании теоремы компенсации для сопротивлений, через которые протекает замкнутый ток J.
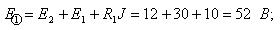
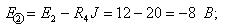
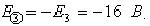
Найденные параметры контуров подставляем в систему контурных уравнений:
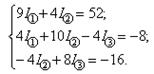
Решив данную систему уравнений, получим значения контурных токов:
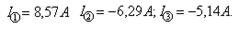
Токи в ветвях определяем путем алгебраического сложения контурных токов и тока источника тока, протекающих по этим ветвям. При этом контурные токи и ток источника тока, направление которых совпадает с направлением тока ветви, берем с положительным знаком, а токи, направление которых противоположно направлению тока ветви – с отрицательным знаком.