Вписанная в треугольник окружность

Свойства вписанной окружности

• В каждый треугольник можно вписать окружность, при этом только одну
• Центр вписанной окружности называется инцентром, он равноудалён от всех сторон
• Центр вписанной окружности является точкой пересечения биссектрис треугольника

Радиус вписанной окружности

Радиус вписанной в произвольный треугольник окружности равен отношению его площади к полупериметру.
Формулы радиуса вписанной окружности:

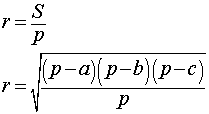
Центр вписанной в треугольник окружности - это точка пересечения биссектрис его улов. При этом стоит заметить, что для равнобедренного треугольника - биссектриса угла напротив основания - является одновременно и высотой.

Четырехугольники

Свойства четырехугольников

Четырехугольник, описанный вокруг окружности (окружность, вписанная в четырехугольник).

Главное свойство описанного четырехугольника:

Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин противоположных сторон равны.

Четырехугольник, вписанный в окружность (окружность, описанная вокруг четырехугольника)

Главное свойство вписанного четырехугольника:

Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы противоположных углов равны 180 градусов.

Существование четырехугольника

Задачи о возможности существования четырехугольника с заданными сторонами

Задача.

Существует ли четырехугольник, если дл:ины сторон 1 см, 3 см, 5 см, 9 см?

Решение.

Для того, чтобы четырехугольник существовал, необходимо, чтобы длина одной из его сторон была меньше, чем сумма длин трех остальных сторон, иначе будет невозможно замкнуть периметр.

Для проверки возьмем наибольшую из сторон (9 см). Тогда сумма остальных составит 1+3+5 = 9 см. Это означает, что длины этих сторон либо должны быт отложены как часть отрезка (9 см) большей стороны, либо такую фигуру замкнуть невозможно. Вывод: такой четырехугольник существовать не может.

Ответ: Нет не существует.

Задача.

Существует ли четырехугольник, если дл:ины сторон 5 см, 17 см, 3 см, 7 см?

Решение.

Для того, чтобы четырехугольник существовал, необходимо, чтобы длина одной из его сторон была меньше, чем сумма длин трех остальных сторон, иначе будет невозможно замкнуть периметр.

Для проверки возьмем наибольшую из сторон (17 см). Тогда сумма остальных составит 7+3+5 = 15 см. Это означает, что такую фигуру замкнуть невозможно. Вывод: такой четырехугольник существовать не может.

Ответ: Нет не существует.

Периметр четырехугольника

Задачи на нахождение периметра четырехугольника

Задача.

Найдите стороны четырехугольника, если его периметр равен 66 см, а одна из сторон больше второй на 8 см и на столько же меньше третьей, а четвертая - в три раза больше второй.

Решение.

Периметр четырехугольника равен сумме длин каждой из его сторон. Для решения задачи обозначим меньшую (!) сторону четырехугольника через x. Для понимания решения, пусть названия сторон будут A, B, C и D. Тогда

A = х + 8 (Одна из сторон четырехугольника, пусть это будет сторона A, больше второй, пусть это будет сторона B на 8 см, соответственно длина меньшей стороны будет x)

B = x (Одна из сторон четырехугольника, пусть это будет сторона A, больше этой стороны на 8 см)

C = x + 16 (... "и на столько же меньше третьей". То есть, если длина стороны A = x + 8, а она меньше третьей на 8 см, то длина стороны C четырехугольника составит x + 16 см)

D = 3x (Длина этой стороны четырехугольника по условию в три раза больше второй)

Соответственно, периметр четырехугольника равен:

P= A + B + C + D

(x + 8) + x + (x + 16) + 3x = 66

6x + 24 = 66

6x = 42

x=7

Соответственно, длины сторон четырехугольника в задаче равны 7, 15, 23, 21

Ответ: 7 см, 15 см, 23 см, 21 см