Нелинейная парная регрессия

Министерство образования и науки РФ

ГОУ ВПО

Российский государственный торгово-экономический университет

Казанский институт

_______________________________________________________

Кафедра информатики и высшей математики

ТАЛЫЗИН В.А.

РУКОВОДСТВО

Для выполнения контрольной работы

По эконометрике

Учебное пособие

КАЗАНЬ-2011г.

Тема 1. Парная регрессия

Линейная парная регрессия

Расчетные формулы

1.1 Оценки коэффициентов модели:

, ,

, , , .

1.2 Выборочные дисперсии и средние квадратические отклонения:

.

1.3 Выборочный коэффициент парной корреляции:

.

1.4 Средний коэффициент эластичности:

.

1.5 Коэффициент детерминации:

.

1.6 Дисперсионное отношение Фишера ( -критерий):

.

1.7 Остаточная сумма квадратов отклонений:

.

1.8 Средняя относительная ошибка аппроксимации:

.

1.9 Стандартная ошибка уравнения регрессии:

.

1.10 Стандартные ошибки параметров регрессии:

.

1.11 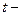статистики Стьюдента параметров уравнения:

.

1.12 Предельные ошибки коэффициентов уравнения, которые с вероятностью (1- 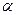), где уровень значимости, не будут превышены:

.

1.13 Доверительные интервалы для коэффициентов уравнения регрессии:

.

1.14 Стандартная ошибка индивидуального прогнозного значения результирующего признака:

.

1.15 Доверительный интервал для прогнозного значения:

.

Решение типовой задачи.

В таблице 1.1 приводятся данные о заработной плате ( 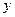, долл.) и возрасте ( , лет) по 20 рабочим.

Табл. 1.1

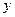Требуется:

1. Построить поле корреляции и сформулировать гипотезу о форме связ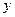и и .

2. Построить линейную регрессионную модель зависимости заработной платы от возраста рабочего, вычислить средний коэффициент эластичности, определить коэффициент детерминации и среднюю относительную ошибку аппроксимации и оценить точность модели.

3. Оценить статистическую значимость параметров регрессии и модели в целом, а также построить интервальную оценку коэффициентов линейной регрессии с надежностью 0,95.

4. Выполнить прогноз заработной платы 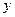для 33-летнего рабочего, оценить точность прогноза, рассчитав стандартную ошибку прогноза и его доверительный интервал.

Решение выполним в среде MS Excel.

1.Сформируем расчетную таблицу следующей структуры:

№ п/п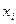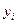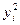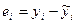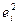
Сумма
Среднее

Введем исходные данные 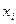, 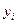в таблицу по столбцам.

Построим поле корреляции при помощи Мастера диаграмм(тип – Точечная диаграмма) и выполним визуальный анализ типа зависимости.

Поле корреляции

По виду поля корреляции можно сделать вывод о том, что форма связи переменных 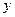и может быть как линейной, так и нелинейной.

2.Рассчитаем колонки , , 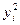расчетной таблицы. Вычисляем суммы и средние значения столбцов с помощью функций СУММ(…)иСРЗНАЧ(…).

Выполним расчет параметров уравнения регрессии по формулам 1.1:

, .

В итоге линейная модель имеет вид:

.

Коэффициент регрессии показывает, что в среднем заработная плата растет на доллара при увеличении возраста рабочего на 1 год.

Найдем значения выборочных дисперсий и СКО по формулам 1.2:

, , , .

Определим выборочный коэффициент корреляции по одной из формул 1.3: .

Коэффициент парной корреляции по шкале Чеддока является высоким, что свидетельствует о существенной зависимости з/п от возраста рабочего.

Вычислим средний коэффициент эластичности по формуле 1.4:

.

Он показывает, что при увеличении возраста рабочего на 1 % от среднего значения з/п в среднем возрастает на 0,799%.

Рассчитаем коэффициент детерминации по формуле 1.5:

.

также близок к единице и по нему следует, что з/п на 72% объясняется таким фактором, как возраст рабочего.

Вычислим предсказанные моделью значения з/п по формуле

и тем самым заполним колонку 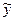расчетной таблицы. Далее вычисляются остатки 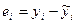и их квадраты 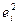. В итоге в строке "Сумма" таблицы определится остаточная сумма квадратов .

Проверим качество модели по средней относительной ошибке аппроксимации, вычислив по формуле 1.8. Для этого в первой строке колонки набираем с использованием функции ABS(…) формулу: =ABS( )*100. После протяжки по всему столбцу вычисляем среднее значение данного столбца:

= .

По видно, что в среднем расчетные значения отклоняются от фактических на 10,2%, что говорит о допустимом качестве модели по этому критерию.

Далее построим график линейной функции на поле корреляции с помощью Мастера диаграмми убедимся, что МНК дал хорошие результаты аппроксимации.

Поле корреляции с линейной регрессией

3.По формулам 1.9 и 1.10 найдем стандартные ошибки уравнения регрессии и его параметров:

, ,

, .

Рассчитаем 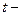статистики Стьюдента по формулам 1.11:

, , .

Обратим внимание на то, что , а .

Найдем с помощью функции СТЬЮДРАСПОБР(…) табличное значение по уровню значимости 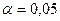и числу степеней свободы . Сравнение расчетных значений с табличным указывает на статистическую значимость параметров 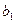и . Параметр же 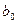не является значимым, поскольку .

Доверительные интервалы строим только для коэффициентов модели, точечные оценки которых являются статистически значимыми. В нашем случае – только для коэффициента регрессии :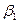

; ; ;

.

Рассчитаем 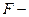критерий Фишера по формуле 1.6:

.

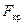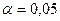Табличное значение = определяем с помощью встроенной статистической функции FРАСПОБР по уровню значимости и числам свободы 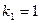и . Поскольку , то можно сделать вывод об адекватности построенной модели.

4.Получим прогнозную заработную плату для 33-летнего рабочего по найденной линейной модели:

(долл.).

Вычислим стандартную ошибку прогнозного значения по формуле 1.14:

.

Находим 95% доверительный интервал для прогнозного значения з/п 33-летнего рабочего с использованием формулы 1.15:

,

.

Таким образом, заработная плата 33-летнего рабочего с вероятностью 0,95 находится в пределах от 220,38 до 382,27 долларов.

Нелинейная парная регрессия

Расчетные формулы

Нелинейная регрессия, линейная по параметрам.

1.2.1 Линеаризация модели выполняется путем введения новых переменных, относительно которых модель будет линейной. Например, если модель имеет вид:

,

то введение новой переменной позволяет получить линейную относительно этой переменной модель:

.

1.2.2 МНК - оценки коэффициентов модели:

, ,

, , , , .

В итоге получается нелинейная парная регрессия .

1.2.3 Выборочная дисперсия и среднее квадратическое отклонение (СКО):

.

1.2.4 Остаточная сумма квадратов отклонений:

.

1.2.4 Индекс корреляции:

.

1.2.5 Индекс детерминации:

.

1.2.6 Средняя относительная ошибка аппроксимации:

.

1.2.7 Средний коэффициент эластичности:

.

1.2.8 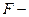критерий Фишера:

,

где число параметров модели.

Нелинейная регрессия, нелинейная по параметрам.

1.2.9 Для линеаризации модели её предварительно логарифмируют и вводят в рассмотрение новые переменные, относительно которых модель будет уже линейной. Рассмотрим, например, степенную модель

.

После логарифмирования она примет вид:

.

Введя новые переменные:

,

получаем линейную модель:

.

1.2.10 МНК - оценки коэффициентов этой модели:

, ,

, , , , .

1.2.11 Оценка коэффициента :

.

В результате получается степенная регрессия .

1.2.12 Факторная сумма квадратов:

1.2.12 Индекс корреляции:

.

1.2.13 Индекс детерминации:

.

Средняя относительная ошибка аппроксимации, средний коэффициент эластичности и 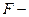критерий Фишера вычисляются по формулам 1.2.6, 1.2.7, и 1.2.8 соответственно.

Решение типовой задачи.

Для данных, представленных в таблице 1.1 требуется:

1. Построить гиперболическую регрессионную модель зависимости заработной платы от возраста рабочего, вычислить индекс корреляции и детерминации, а также статистическую значимость уравнения регрессии на уровне .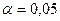

2. Построить степенную регрессионную модель зависимости заработной платы от возраста рабочего, оценить её точность по индексу детерминации и средней относительной ошибки аппроксимации и значимость (на уровне ).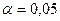

3. Сравнить модели парной регрессии (включая линейную) по индексу детерминации и средней относительной ошибки аппроксимации и выбрать наилучшую.

Решение выполним в среде MS Excel.

1.Оценим гиперболическую модель . Она линейна по параметрам .

Введем новую переменную . Линеаризованная модель примет вид: .

Сформируем расчетную таблицу следующей структуры:

№ п/п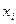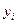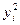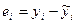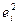
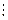Сумма
Среднее

Введем исходные данные 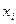, 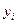в таблицу по столбцам и рассчитаем колонки , , , 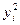. Вычисляем суммы и средние значения столбцов с помощью функций СУММ(…)иСРЗНАЧ(…).

Выполним расчет параметров уравнения регрессии по формулам 1.2.2:

, .

В итоге получена гиперболическая модель: .

Вычислим предсказанные моделью значения з/п по формуле

и тем самым заполним колонку расчетной таблицы. Далее вычисляются остатки 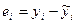и их квадраты 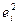. В итоге в строке "Сумма" колонки 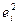таблицы определится остаточная сумма квадратов .

Построим график функции на поле корреляции с помощью Мастера диаграмми убедимся, что МНК дал хорошие результаты аппроксимации.

Найдем значения выборочной дисперсии и СКО для 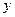по формулам 1.2.3:

, .

Найдем индекс корреляции по формуле 1.2.4:

.

Индекс корреляции близок к единице и это указывает на тесную гиперболическую связь между изучаемыми признаками.

Рассчитаем индекс детерминации по формуле 1.2.5:

.

Значение индекса детерминации близко к единице и по нему следует, что з/п по этой модели на 78% обусловлена таким фактором, как возраст рабочего.

Проверим качество модели по средней относительной ошибке аппроксимации, вычислив по формуле 1.2.6. Для этого в первой строке колонки набираем с использованием функции ABS(…) формулу: =ABS( )*100. После протяжки по всему столбцу вычисляем среднее значение данного столбца:

= .

По видно, что в среднем расчетные значения отклоняются от фактических на 8,7%, что говорит о хорошем качестве модели по этому критерию.

Вычислим средний коэффициент эластичности по формуле 1.2.7:

Найдем производную

.

Отсюда

.

Он показывает, что при увеличении возраста рабочего на 1 % от среднего значения з/п в среднем возрастает на 0,74%.

Рассчитаем 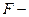критерий Фишера по формуле 1.2.8 (в нашем случае ):

.

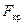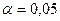Табличное значение = определяем с помощью встроенной статистической функции FРАСПОБР по уровню значимости и числам свободы 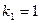и . Поскольку , то можно сделать вывод о хорошей аппроксимации статистических данных построенной моделью.

2.Построим степенную модель . Эта модель является нелинейной по параметру .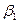

Выполним преобразования по формулам 1.2.9. Линеаризованная модель примет вид: . Здесь , .

Сформируем расчетную таблицу следующей структуры:

№ п/п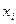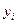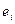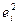

(

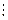Сумма

Среднее

Введем исходные данные 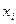, 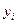в таблицу по столбцам и рассчитаем колонки , , , . Вычисляем суммы и средние значения столбцов с помощью функций СУММ(…)иСРЗНАЧ(…).

Выполним расчет параметров уравнения регрессии по формулам 1.2.10:

, .

Найдем оценку коэффициента с использованием функции EXP(…):

.

В результате построена степенная модель .

Вычислим на основе модели значения з/п по формуле:

с использованием встроенной функции СТЕПЕНЬ( 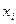; ). В итоге будет заполнена колонка таблицы.

Далее вычисляются остатки 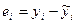, их квадраты 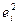, разности , а также их квадраты . В итоге в строке "Сумма" колонки таблицы определится факторная сумма квадратов .

Построим график функции на поле корреляции с помощью Мастера диаграмми убедимся, что кривая неплохо представляет искомую зависимость.

Найдем индекс корреляции по формуле 1.2.12 (значение определено ранее):

.

Близость индекса корреляции к единице указывает на тесную степенную связь между изучаемыми признаками.

Рассчитаем индекс детерминации по формуле 1.2.13:

.

Из значения индекса детерминации следует, что з/п по этой модели на 84% обусловлена возрастом рабочего.

Оценим качество модели по средней относительной ошибке аппроксимации, вычислив по формуле 2.6:

= .

По видно, что в среднем расчетные значения отклоняются от фактических на 9,9%, что говорит о неплохом качестве модели по этому критерию.

Вычислим средний коэффициент эластичности по формуле 1.2.7:

Найдем производную:

.

Отсюда

.

Из этого следует, что при увеличении возраста рабочего на 1 % от среднего значения з/п в среднем возрастает на 0,86%.

Рассчитаем 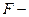критерий Фишера по формуле 1.2.8:

.

Табличное значение 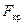= уже ранее определено. Так как выполняется неравенство , то можно сделать вывод о надежности и статистической значимости степенной модели.

3.Для сравнения двух нелинейных моделей составим итоговую таблицу со значениями средней относительной ошибки аппроксимации и индекса детерминации:

Модель
Гиперболическая	8,73	0,778
Степенная	9,90	0,844
Линейная	10,16	0,72

Из таблицы видно, что по средней ошибке аппроксимации лучшей является гиперболическая модель, а по индексу детерминации – степенная. Но по этим показателям они обе лучше линейной модели. Для практического использования можно рекомендовать степенную модель.