ТригонометриялыҚ функциялар

Алматы 2012жыл

Жоспары:

Кіріспе бөлім:

Негізгі бөлім:

А)Есеп шығарудың кейбір әдістері.

Ә) Тринонметриялық функцияларға арналған есептер

Б)Теңдеулер және теңсіздіктер жүйесіне арналған есептер

В)Көрсеткіштік және логарифмдік теңдеулерге арналған есептер

Қорытынды бөлім:

Пайдаланылған әдебиеттер:

ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯЛАР

§1. Таблицасыз есептеу.

Таблицасыз есептеу дегеннің мағынасын - В.М.Брадис таблицасын пайдаланбай, түрлі тригономертриялық формулалар мен жасанды әдістерді, аргументтің белгілі мәніндегіфункцияның мәнін қолданып ізделінді санды табу.

Мысалы, 4. Таблицасыз =ты есепте десе былай орындаймыз.

1-әдіс. 45 ты 45 пен 30 =тың айырымы ретінде қарастырып, косинус үшін қосу формуласын пайдаланамыз да негізгі бұрыштардың тригономериялық функцияларының шамаларын пайдаланамыз:

15

2-әдіс.15°=ты 30° =тың жартысы екенін ескеріп, жарты аргументтің формуласын қолдануға болады:

2. қосындысын есептеп шығарыңдар.

Шешу.

аргумент формуласын екі рет пайдаланғаннан кейін,өрнектің алымы үшін келтіру формуласын қолданамыз. Сонда бөлшектің алымы мен бөлімі ықшамдалатын өрнекке келеді.

Сонымен,

3. өрнегінің сан мәнін табыңдар.

Шешу. Өрнекті ортақ бөлімге келтіріп, екеніні ескеріп, одан әрі tg60° 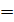ты бөлшек ретінде жазып түрлендіріп, қосу формуласын т.б. пайдаланамыз:

4. көбейтіндісін есептеңдер.

Шешу. Ол үшін геометриядан белгілі бірлік шеңберді іштей сызылған дұрыс n–бұрыштың қабырғасы мен апофемасын есептеу формуласын пайдалануға болады. Формула бойынша

Мұндағы 2 – дұрыс n–бұрыштың қабырғасы, дұрыn-бұрыштың апофемасы n-қабырғалар саны. Біздің мысалымызда n Олай болса, және

Сонымен,

Демек,

5. көбейтіндісін есептеңдер.

Шешу.

Мұндағы

болғандықтан соңғы теңдікті

қысқартып,

Ақырында,

екенін ескерсек

2-әдісі.

Жаттығулар:

6. және 7.

8. 9.

10. 10.

11. 12.

13. 14.

15. 4 16.

17. 18.

19. 20.

21.

22. 23.

24.

25.tg20 26.

27. tg20 28.

29.tg10 30.tg5

31.ctg9 32.tg9

33.tg21

34. Егер екендігім белгілі болса неге тең болады?

35. көбейтіндісін есептеп шығарыңдар.

36. Ескерте кететін нәрсе, таблицасыз есептеу-тепе-тең түрлендіру есептерінің дербес түрлері екендігі.

§2.Теңдеулерді шешу.

Тригонометриялық теңдеулерді шешу әдістеріне бірнеше мысал келтірейік.

1.

1-әдіс. Теңдеудің екі жақ бөлігін де квадраттасақ және

екенін ескерсек, берілген теңдеу мына түрге келеді:

Бұл толық квадрат теңдеуді шешіп, және екендігін табамыз. Соңғы тригонометриялық теңдеулердің шешімдері сәйкес болады.

2-әдіс. Берілген теңдеудің екі жақ бөлігін де мүшелеп бөліп, теңдеуін шығарып аламыз.

Мұнда

демек,

келтіру формуласын пайдалансақ:

немесе

Енді синустар айырымын көбейтінді түріне келтіреміз:

Мұнан

немесе

Бұл табылған х-тер 1-әдіспен табылған шешімдермен бірдей, тек түрі басқаша жазылған.

2.

Шешу. Бірінші мен үшінші, екінші мен төртінші қосылңыштарды топтап, синустар қосындысын көбейтңндңге келтіріп, косинус жұп функция екенін ескерсек және ортақ көбейткіш жақша сыртына шығарғаннан кейін бастапқы теңдеу мына түргее келеді:

Мұнан

0

немесе

Екінші теңдеуді шешу үшін қосындыны көбейтінді түріне келтіреміз:

2

мұнан

немесе

3. tg теңдеуін шешіңдер.

Шешу. tg2 формуласын пайдаланып tgx–ті жарты бұрыштың тангенсі түрінде жазамыз да ықшамдаймыз. Сонда мына көбейтіндіге келеді:

1

немесе

2tg3

x1 x2 болғандықтан, есептің жауабы

Бірақ мынаны ескерген дұрыс. Тангенс функциясының бас мәні -ні берілген теңдеуге қойғанда теңдеудің мағынасы жойылады. Алайда, берілген теңдеудің өзіндік емес шешімдері болады. Мұны былай түсіну керек. Егер де теңдеудің екі жақ бөлігінен шек алып, х-ті ұмтылдырғанда оң жақ бөлігі мен сол жақ бөліктерінің шектері өзара тең болады.

4. 3^lgtgx +3 ^lgctgx=2

Шешу. 1-әдіс. х-тің мүмкін мәндер жиыны қос теңсіздігімен анықталады, өйткені: біріншіден, х Бұл мәндерде тангенстің не котангенстің мәні болайды; екіншіден, тангенс пен котангенстің екеуі де оң сандар, яғни х бірінші не үшінші ширекте анықталуы керек, басқаша жағдайда олардың логарифмдері қарастырылмайды.

3^lgtgx пен 3 ^lgctgxөзара кері шамалар, өйткені олардың көбейтіндісі 1-ге тең. Сондықтан берілген теңдеудің сол жақ бөлігінің мүшелерінің қосындысы екіден кем емес, яғни

3^lgtgx +3 ^lgctgx 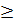2

Олай болса теңсіздік өзінің ең кіші мәнін қосылғыштардың әрқайсысы 1 болғанда ғана қабылдайды:

3^lgtgx=1 және 3^lgctgx=1

Мұнан

lgtgx=0

және

lgctgx=0

Теңдеудің ортақ шешімі

2-әдіс. ctgx= болғандықтан, lgctgx=lg . Олай болса бастапқы теңдеуді мына түрде жазуға болады:

3^lgtgx +3 ^-lgtgx=1

Егер 3^lgtgx =y десек, соңғы теңдеу келтірілген квадрат теңдеуге келеді. Оны шешіп, бастапқы белгісізге оралсақ, х-ті табу оңай:

3^lgtgx=1 lgtgx=0

Жаттығулар:

5. 6.

7. ²8.tgx=2

9.

10.

11. 12. 3tg2x-

13.tgx- 14.

15.

16.

17.

18. 19.

20.

21. 22.

23.2 24.2

25.

26.1+2

27.

28.

29.3

30.

31.

32.

33.

34.

35.tg2x=

36.

37.tg2x=

38.

39.

40.

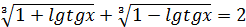
41.

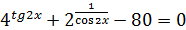
42.

43.

44.

45.tg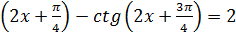

46.tgx2*sin5x-cos5x=0

47.

§3.Теңдеулер системасын шешу. Мысал келтірейік.

Шешу. Системаның екінші теңдеуін түрлендіріп, біріншісін пайдалансақ мынау шығады:

Соңғы қатынасты ескерсек, бастапқы система тына түрге келеді:

Системаның екінші теңдеуінен бірінші теңдеуін шегеріп және оларды қосып мына системаға келеміз:

х+у= демекx=

x-y=2l y=

Жауабы:{х y=

2. x+y=

tgx*tgy=

Шешу. Системаның бірінші теңдеуіндегі х+у пен өзара тең болғандықтан, олардың тангенстері де тең болады. Сондықтан tg tgx+tgy= болады. Сонда бастапқы система төмендегі системаға келеді.

tgx+tgy=

tgx*tgy=

Виета теоремасы бойынша tgxпенtgy квадраттеңдеуінің түбірлері. Бұл теңдеуді шешіп, tgx= , tgy= екенін табамыз. Мұнанx=arctg . Бұл бастапқы системаның шешімі.

Жаттығулар:

3. 4.x+y=135

tgx-tgy=2

5. 6. x+y=60

tgx*tgy=

7. 8.

=4 tgx=5tgy

9. x+y= 10.

tgx*tgy=

§4. Теңсіздіктерді шешу.

1-мысал.

Шешу. Қосындыны көбейтіндіге келтіру формуласын пайдалансақ 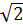көбейткіші қысқарады да мына түрге келеді:

Синус тек 1,2 ширектерде оң мәндер қабылдайтынтықтан

немесе

2-мысал. Берілген теңсіздікті мына түрге қайта жазайық:

Соңғы теңсіздік -2<tgx<-1 теңсіздігі орындалса ғана, тек сонда ғана орындалады. Демек, берілген теңсіздіктің шешімдері