Приближенный метод решения дифференциальных уравнений С.А. Чаплыгина

Метод, разработанный академиком С.А. Чаплыгиным для приближенного интегрирования обыкновенных дифференциальных уравнений, является одним из самых сильных и простых по идее. Студент, выполняющий курсовую работу, обязан подробно изложить основные идеи этого способа и проиллюстрировать их на соответственно подобранных примерах.

Для более глубокого изучения можно рекомендовать две статьи [3] и [4] акад. Н.Н. Лузина, перепечатанные в III томе его собрания сочинений.

В своем учебнике для втузов [5] Н.Н. Лузин дал чрезвычайно простое популярное изложение метода Чаплыгина.

Литература:

[1]. С.А. Чаплыгин. Новый метод приближенного интегрирования дифференциальных уравнений. – ГИТТЛ, 1950.

[2]. И.С. Березин и Н.П. Жидков. Методы вычислений, т.2. – Физматгиз, 1959.

[3]. Н.Н. Лузин. О методе приближенного интегрирования академика С.А. Чаплыгина. – Труды ЦАГИ, вып. 141, 1932.

[4]. Н.Н. Лузин. О методе приближенного интегрирования академика С.А. Чаплыгина. Журнал «Успехи математических наук», т.6, вып. 6, 1951.

[5]. Н.Н. Лузин. Интегральное исчисление. – «Советская наука», 1955.

Начала операционного исчисления

Операционное исчисление возникло в прошлом веке как особый метод решения некоторых важных для практических классов обыкновенных дифференциальных уравнений. Строгое обозначение оно получило недавно и теперь широко применяется для решения линейных дифференциальных уравнений (электроника, гидромеханика, теплотехника и т.п.). Очень простое изложение его начал имеется в [1] (гл. XVII, § 8-12, стр. 222-244). Студент обязан изложить основные принципы операционного исчисления и пояснить их примерами.

Для более подробного изучения вопроса можно рекомендовать [2] и особенно [3]. Очень своеобразное, глубокое и вместе с тем простое изложение имеется в [4].

Литература:

[1]. Г.П. Толстов. Курс математического анализа, т. II. – ГИТТЛ, 1957.

[2]. Х. Карслоу и Д. Егер. Операционные методы в прикладной математике. – ИЛ, 1948.

[3]. М.А. Лаврентьев и Б.В. Шабат. Методы теории функций комплексного переменного. – Физматгиз, 1958.

[4]. Ян Микусинский. Операционное исчисление. – ИЛ, 1956.

Методы решения систем обыкновенных дифференциальных уравнений

Задачей работы является изложение основных методов решения систем дифференциальных уравнений и решение этими методами задач, подобранных руководителем. Вполне доступное изложение этого материала имеется в рекомендуемой книге Л.Э. Эльсгольца (гл. III, § 1-5). Несколько более подробное изложение – в книгах [2] и [3].

Литература:

[1]. Л.Э. Эльсгольц. Дифференциальные уравнения. – ГИТТЛ, 1957.

[2]. В.В. Степанов. Курс диффернциальных уравнений. – ГИТТЛ, 1950.

[3]. Дж. Сансоне. Обыкновенные дифференциальные уравнения. – ИЛ, 1953-1954.

Бесселевы функции

Среди специальных функций – цилиндрические, или бесселевы, являются едва ли не важнейшими и особенно хорошо изученными. При построении их теории весьма заметную роль сыграл академик Сонин.

Работа над темой предполагает изучение решения дифференциального уравнения Бесселя

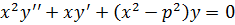
Методом Фробениуса. Для этого следует сначала прочесть § 4, гл. II, [1] (стр. 132-144), а затем гл. II, [2] (стр. 17-27).

Работу над темой целесообразно завершить решением ряда примеров, например № 1, 9, 10, 12, помещенных на стр. 27 [2]. Для более подробного изучения вопроса рекомендуются [3] и [2].

Литература:

[1]. В.И. Смирнов. Курс высшей математики, т.2, изд. 17. – Физматгиз, 1961.

[2]. Э. Грей и Г.Б. Матьюз. Функции Бесселя и их приложения к физике и механике, изд. 2. – Иниздат, 1953.

[3]. Р.О. Кузьмин. Бесселевы функции, изд. 2. – ОНТИ, 1935.