Предпосылки метода наименьших квадратов
При оценке параметров уравнения регрессии применяется МНК. При этом делаются определенные предпосылки относительно составляющей 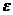
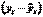 , которая представляет собой в уравнении
, которая представляет собой в уравнении 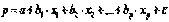 ненаблюдаемую величину.
ненаблюдаемую величину.
Исследования остатков εi предпол-ют проверку наличия следующих 5 предпосылок МНК:
1) случайный характер остатков. С этой целью строится график отклонения остатков от теоретических значений признака. Если на графике получена горизонтальная полоса, то остатки представляют собой случайные величины и применение МНК оправдано. В других случаях необходимо применить либо другую функцию, либо вводить дополнительную информацию и заново строить уравнение регрессии до тех пор, пока остатки не будут случайными величинами.
2) нулевая средняя величина остатков, т.е. 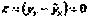 , не зависящая от хi. Это выполнимо для линейных моделей и моделей, нелинейных относительно включаемых переменных. С этой целью наряду с изложенным графиком зависимости остатков εi от теоретических значений результативного признака уx строится график зависимости случайных остатков εi от факторов, включенных в регрессию хi. Если остатки на графике расположены в виде горизонтальной полосы, то они независимы от значений xj. Если же график показывает наличие зависимости εi и xj то модель неадекватна. Причины неадекватности могут быть разные.
, не зависящая от хi. Это выполнимо для линейных моделей и моделей, нелинейных относительно включаемых переменных. С этой целью наряду с изложенным графиком зависимости остатков εi от теоретических значений результативного признака уx строится график зависимости случайных остатков εi от факторов, включенных в регрессию хi. Если остатки на графике расположены в виде горизонтальной полосы, то они независимы от значений xj. Если же график показывает наличие зависимости εi и xj то модель неадекватна. Причины неадекватности могут быть разные.
3) Гомоскедастичность - дисперсия каждого отклонения εi одинакова для всех значений xj. Если это условие применения МНК не соблюдается, то имеет место гетеро-сть. Наличие гетеро-сти можно наглядно видеть из поля корреляции.
4) Отсутствие автокорреляции остатков. Значения остатков εi распределены независимо друг от друга. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих наблюдений. Отсутствие автокорреляции остаточных величин обеспечивает состоятельность и эффективность оценок коэффициентов регрессии.
5) Остатки подчиняются нормальному распределению.
В тех случаях, когда все пять предпосылок выполняются, оценки, полученные по МНК и методу максимального правдоподобия, совпадают между собой. Если распределение случайных остатков εi не соответствует некоторым предпосылкам МНК, то следует корректировать модель, изменить ее спецификацию, добавить (исключить) некоторые факторы, преобразовать исходные данные, что в конечном итоге позволяет получить оценки коэффициентов регрессии aj, которые обладают свойством несмещаемости, имеют меньшее значение дисперсии остатков, и в связи с этим более эффективную статистическую проверку значимости параметров регрессии.
