Теорема про вкладені відрізки
Нехай задана послідовність відрізків
, де 
(4)
для всіх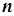 
, таких, що кожний наступний міститься в попередньому і при зростанні 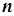довжина 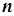-ного відрізка прямує до нуля, тобто 
. Таку послідовність називатимемо послідовністю вкладених відрізків.
Теорема. Для будь-якої послідовності вкладених відрізків існує єдина точка, яка належить усім відрізкам даної послідовності.
Доведення. З означення вкладених відрізків випливає, що їх ліві кінці утворюють неспадну послідовність
, (5)
а праві – незростаючу
. (6)
При цьому послідовність (5) обмежена зверху, а послідовність (6) обмежена знизу, оскільки 
і 
. Отже, ці послідовності мають границі. Нехай 
. За умовою , а тому
.
Отже, 
. Покладемо 
. Тоді 
для всіх 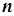, тобто точка 
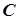належить усім відрізкам (4).
Покажемо, що така точка єдина. Припустимо, що існує точка 
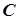, відмінна від точки і така, що належить усім відрізкам (4). Тоді для будь-якого 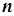повинна виконуватися нерівність 
, з якої випливає , що 
, що суперечить умові.
Зазначимо, що теорема не справджується, якщо замість відрізків розглядати інтервали 
, наприклад для послідовності вкладених інтервалів
(6)
яку б точку 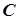з інтервалу 
не взяти, вона не буде належати всім інтервалам (6).
ЛЕКЦІЯ 8
13. Теорема про вкладені відрізки.
14. Підпослідовність числової послідовності.
15. Теорема Больцано - Вейєрштрасса.
16. Критерій Коші збіжності числової послідовності.
Теорема про вкладені відрізки.
Нехай задана послідовність відрізків
, де (4)
для всіх 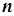, таких, що кожний наступний міститься в попередньому і при зростанні 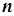довжина 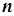-ного відрізка прямує до нуля, тобто . Таку послідовність називатимемо послідовністю вкладених відрізків.
Теорема. Для будь-якої послідовності вкладених відрізків існує єдина точка, яка належить усім відрізкам даної послідовності.
Доведення. З означення вкладених відрізків випливає, що їх ліві кінці утворюють неспадну послідовність
, (5)
а праві – незростаючу
. (6)
При цьому послідовність (5) обмежена зверху, а послідовність (6) обмежена знизу, оскільки і . Отже, ці послідовності мають границі. Нехай . За умовою , а тому
.
Отже, . Покладемо . Тоді для всіх 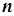, тобто точка 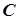належить усім відрізкам (4).
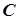Покажемо, що така точка єдина. Припустимо, що існує точка , відмінна від точки і така, що належить усім відрізкам (4). Тоді для будь-якого 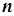повинна виконуватися нерівність , з якої випливає , що , що суперечить умові.
Зазначимо, що теорема не справджується, якщо замість відрізків розглядати інтервали , наприклад для послідовності вкладених інтервалів
(6)
яку б точку 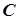з інтервалу не взяти, вона не буде належати всім інтервалам (6).