Обратимые и обратные отображения

Определение 1. Отображение 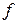: 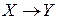называется взаимнооднозначным соответствием или биекцией, если прообраз любого элемента 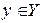состоит только из одного элемента 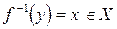. Равносильное условие: для любого 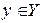уравнение 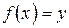имеет только одно решение .

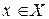Например, отображение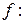

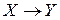
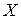
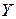
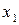
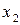
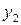
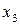
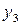
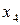
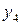
является биективным.

Определение 2. Отображение 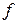: 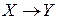называется обратимым, если существует отображение 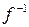: 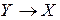, такое, что

, ,

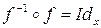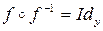где , ,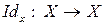

, .

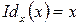
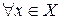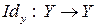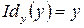
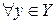Отображение 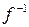называется обратным к .

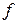Теорема (равносильность условий биективности и обратимости). Отображение 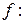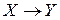обратимо тогда и только тогда, когда оно биективно.

Доказательство. Пусть отображение 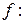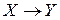биективно, тогда прообраз любого элемента 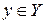состоит только из одного элемента 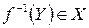. Тем самым определено некоторое отображение 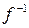: 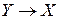. Покажем, что , .

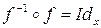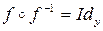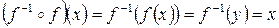
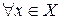, т.е.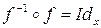

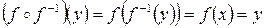
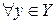, т.е. .

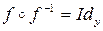Таким образом, отображение обратимо.

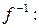
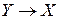Обратно, пусть отображение - обратимо, т.е. существует отображение и , .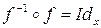

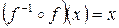Применим к уравнению 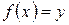отображение :

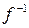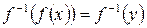или .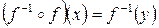

В силу обратимости отображения имеем

.

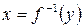
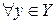Таким образом, уравнение 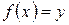имеет единственное решение 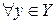и, следовательно, ­- биекция.

Отметим, что если 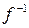: 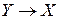обратная к , то функция : 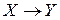является обратной к 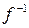. Поэтому функции и 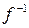называются взаимнообратными.

Примеры.

1. Рассмотрим 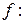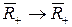, , 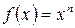где .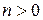

Для 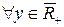уравнение 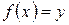имеет единственное решение 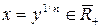, поэтому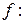 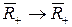обратимо и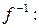 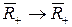определяется равенством

.

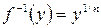2. Покажем, что отображение 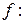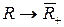, 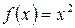не обратимо.

Действительно, 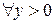уравнение 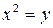имеет два решения 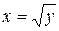, . Поэтому отображение 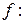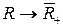не обратимо.

3. Отображение 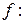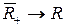, 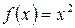не обратимо, так как 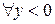уравнение 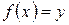не имеет решений.