Задачи для самостоятельного решения. 3.1.Изобразите с помощью столбиковой диаграммы данные о расходах на социально-культурные мероприятия из государственного бюджета Украины

3.1.Изобразите с помощью столбиковой диаграммы данные о расходах на социально-культурные мероприятия из государственного бюджета Украины, млрд. грн.:

1998 1999 2000 2001

13,1 13,5 19,1 25,5

3.2. С помощью квадратной диаграммы сопоставьте следующие данные об инвестициях в жилищное строительство Украины по формам собственности за 2001 год, млн.грн.: частная - 705; коллективная - 561; государственная - 409; коммунальная - 265.

3.3. По данным о вводе в эксплуатацию жилья в Украине (в кв.м в расчете на 1 тыс.чел. населения) в 1995 – 2001 гг. постройте столбиковые и секторные диаграммы.

м² на 1000 чел

Площадь жилых домов	1995 г.	1998 г.	1999 г.	2000 г.	2001 г.
Всего
в городских поселениях
в сельских местностях

3.4. По данным о грузообороте Украины постройте: 1) квадратные, 2) круговые, 3) секторные диаграммы:

млрд. т/км

Виды транспорта	1995 г.	2001 г.
Все виды транспорта, в том числе:		393,8
- железнодорожный	195,8	177,5
- морской	123,1	10,1
- речной	5,7	3,7
- автомобильный	34,5	18,3
- трубопроводный	184,9	184,2

3.5. Изобразите графически с помощью фигур-знаков данные о производстве холодильников (тыс.шт.) в Украине за 1995-2001 гг.

1995 1998 1999 2000 2001

562,5 389,5 409,4 450,9 508,5

3.6.Постройте знаки Варзара по следующим данным о вкладах населения в сберегательном банке области на конец 2001г: 1) число вкладов - 106,6 тыс.: а) в городских поселениях - 78,9; б) в сельских местнос-тях - 27,7; 2) сумма вкладов - 91,0 млн.грн.: а) в городских поселениях - 66,1; б) в сельских местностях - 24,9; 3) средний размер вклада - 854,0 грн.: а) в городских поселениях - 837,0; б) в сельских местностях- 900,0.

3.7.Постройте линейные диаграммы, характеризующие динамику внешней торговли Украины:

Показатели	1995г	1996г	1997г	1998г	1999г	2000г	2001г
Внешнеторговый оборот	31,8	32,0	31,3	27,3	23,4	28,6	32,1
Экспорт	15,7	14,4	14,2	12,6	11,6	14,6	16,3
Импорт	16,1	17,6	17,1	14,7	11,8	14,0	15,8

3.8.Продажа отдельных товаров на колхозных рынках города по месяцам 2002 г. характеризуется следующими данными:

Месяцы	Картофель, тыс.т	Молоко, тыс.л.	Месяцы	Картофель, тыс. т	Молоко, тыс.л.
Январь	2,4		Июль	14,9
Февраль	3,7		Август	11,7
Март	3.8		Сентябрь	14,0
Апрель	5,5		Октябрь	11,4
Май	5.2		Ноябрь	6,6
Июнь	9,7		декабрь	6,5

Постойте радиальную диаграмму. Проведите анализ полученных результатов.

3.9. По областям Украины по состоянию на 01.01.2001г. имеются следующие данные:

Области	Территория, тыс.км2	Численность населения,тыс.чел
Донецкая	26,5	4893,6
Днепропетровская	31,9	3678,0
Запорожская	26,7	2607,4
Кировоградская	27,2	1983,9
Луганская	24,6	1152,9

Постройте картограмму “плотность населения” по областям Украины: а) точечную, б) фоновую. Что показывает построенная картограмма?

3.10.По восьми административным районам области об урожайности и посевных площадях озимого ячменя постройте: 1) картограмму урожайности с помощью штриховки; 2) точечную картограмму посевных площадей.

Номер района	Посевная площадь, га	Урожайность озимого ячменя, ч с 1 га	Номер района	Посевная площадь, га	Урожайность озимого ячменя, ч с 1 га
	14,1	17,5		15,9	31.6
	9,2	20,1		2,6	18,1
	10,2	36,1		9,3	24,3
	3,1	27,2		17,4	26,3

Тема 4. Статистические показатели

Методические указания

При анализе статистической информации применяется система обобщающих показателей: абсолютных, относительных и средних величин.

Абсолютные величины выражают размеры, объемы явлений или процессов. Их получают непосредственно в результате статистического наблюдения, сводки и группировки данных, а также в результате специальных расчетов. К абсолютным показателям, например, относится площадь территории страны, объем промышленного производства, число предприятий и т.п.

Абсолютные статистические показатели всегда являются числами именованными. В зависимости от социально-экономической сущности исследуемых явлений, их физических свойств они выражаются в натуральных и условно-натуральных, трудовых и стоимостных единицах измерения.

В международной практике используются такие натуральныеединицы измерения, как тонны, килограммы, литры, километры, мили, баррели, штуки и т.д.

Условно-натуральные измерители используются в тех случаях, когда какой-либо продукт имеет несколько разновидностей и общий объем можно определить только исходя из общего для всех разновидностей потребительского свойства. Так, различные виды топлива переводят в условное топливо с теплотворной способностью в 7000 ккал/кг, мыло разных сортов – в условное мыло с 40 %-м содержанием жирных кислот и т.п. Перевод в условные единицы измерения осуществляется на основе коэффициентов, рассчитываемых как отношение потребительских свойств отдельных разновидностей продукта к эталонному значению: .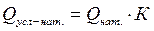

Трудовые единицы измерения применяют, в основном, для определения единиц измерения рабочего времени (чел-час, чел-день).

В условиях рыночной экономики особое значение имеют стоимостныеединицы измерения, позволяющие дать денежную оценку социально-экономическим объектам и явлениям.

Относительная величина- это обобщающий статистический показатель, характеризующий количественное соотношение двух величин в пространстве (между объектами), во времени (по одному и тому же объекту) или сравнения показателей разных свойств изучаемого объекта.

Относительные показатели получаются путем деления одной статистической величины на другую. В числителе всегда находится сравниваемый показатель, а в знаменателе – показатель, с которым производится сравнение (база сравнения). База сравнения выступает в качестве своеобразного измерителя. В зависимости от числового значения базы сравнения, результат отношения может быть выражен в коэффициентах, процентах, промилле (⁰/₀₀), продецимилле (⁰/₀₀₀), а также может быть числом именованным.

В статистике вычисляют следующие относительные величины:

1.Относительная величина планового задания - отношение величины показателя, устанавливаемого на планируемый период или обусловленной договором к его величине, достигнутой за предшествующий (базисный) период: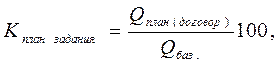

где Q_план и Q_баз – плановый и базисный размеры явления за период.

2. Относительная величина выполнения плана (нормы или договорных обязательств) - результат сравнения фактически достигнутого уровня показателя в текущем (отчетном) периоде с его плановым уровнем или нормативным, или уровнем, обусловленным договором. Если показатели заданы в абсолютном выражении:

,

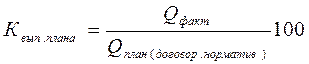где Q факт – фактический объем явления за отчетный период.

3. Относительная величина динамики характеризует степень изменения изучаемого явления во времени, то есть в отчетном периоде по сравнению с базисным (сравниваются фактические уровни):

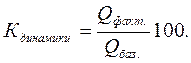
Рассмотренные относительные величины взаимосвязаны между собой: К_{динамики} = К_{план. задания} · К_{вып. плана}

4. Относительная величина структуры характеризует состав совокупности, показывает, какой удельный вес (долю) во всей совокупности составляют ее части. Определяется как отношение размеров частей к целому: d = 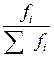(100).

5. Относительная величина координации – соотношение частей целого между собой. За базу сравнения принимают одну из составных частей целого, а затем находят отношение всех частей к ней. Показывает, сколько единиц данной части целого приходится на 1, 10, 100, 1000 и т.п. единиц части, принятой за базу сравнения:

K_{координации} = K₁ : K₂ :... : K _баз , ,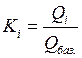

где Q_баз– уровень, принятый за базу сравнения; Q₁+ Q ₂+...+ Q_баз=Q_целое

6.Относительная величина интенсивности характеризует сте-пень распространения или развития какого-либо явления в определенной совокупности, с ним связанной. Получается сопоставлением разноименных абсолютных величин, связанных в своем развитии, но относящихся к различным совокупностям (производительность труда, фондоотдача, рентабельность, демографические коэффициенты, социальные показатели и т.д.)

7. Относительная величина сравнения – отношение одноименных величин, относящихся к разным объектам или территориям, взятое, как правило, за одно и то же время. Выражается в коэффициентах.

Средняя величина– этообобщающий показатель, который характеризует типичный уровень варьирующего признака в расчете на единицу однородной совокупности. Она рассчитывается путем деления объема признаков на число единиц, обладающих данным признаком. Поэтому в общем виде формально это соотношение может быть представлено в форме агрегатной средней: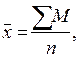

где SM – объем явления или объем признака; n – объем совокуп-ности, т.е. число единиц, обладающих данным признаком.

В практике статистической обработки материалов возникают различные задачи. Для их решения требуются разные виды средних. В статистике вычисляют следующие виды средних величин:

1) среднюю арифметическую; 4) моду и медиану;

2) среднюю гармоническую; 5) среднюю хронологическую[1];

3) среднюю квадратическую; 6) среднюю геометрическую².

Указанные средние величины можно объединить в две группы: степенные средние (средняя арифметическая, средняя гармоническая, средняя квадратическая и средняя геометрическая) и структурные средние (мода и медиана). Общая формула степенной средней имеет вид: ,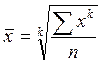

где k - показатель степени средней.

При k = -1 - средняя гармоническая; k = 0 - средняя геометрическая;

k = 1 - средняя арифметическая; k = 2 - средняя квадратическая.

Признак, по которому находится средняя, называется осредняемым признаком и обозначается 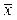. Величины осредняемого признака у каждой единицы совокупности называются индивидуальными его значениями или вариантами. Обозначаются как x₁, x₂, x₃, …x_n.. Частота (повторяемость) индивидуальных значений признака – f (статистический вес).

Каждая средняя в зависимости от характера представления исходных данных рассчитывается двумя способами – как простая и как взвешенная. Если признак не сгруппирован, то применяется форма простой средней; если признак заранее сгруппирован, то применяется форма взвешенной средней.

Средняя арифметическая простая: ,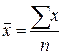

где n – количество единиц совокупности (n = åf)

Средняя арифметическая взвешенная: ,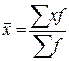

где åxf = åM – объем явления.

Весами могут быть и частости, т.е относительные величины структуры (доли), выраженные в процентах или коэффициентах.

Тогда: 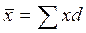(если d - доля, выраженная в коэффициентах):

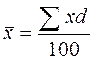(если d – в процентах)

В интервальных вариационных рядах значение признаков дано в виде интервалов “от … до …”. Для расчета средней в этом случае необходимо перейти к дискретному ряду, т.е. в каждом интервале найти среднее значение (x), а затем расчет выполнять по средней арифметической взвешенной: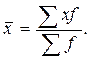

Средняя гармоническая – это величина, обратная средней арифметической. Применяется, если заданы объемы явлений (объемы признаков), но не известны частоты. По способу расчета средняя гармоническая бывает:

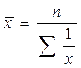- простая, применяется, когда объемы признака (n) равны.

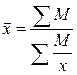- взвешенная, применяется, когда известны индивидуальные значения признака (х), но не заданы веса (f), которые входят сомножителем в известный объемный показатель (М = х f).

В практической работе часто возникает задача выбора формы средней величины между средней арифметической взвешенной и средней гармонической взвешенной. Для этого необходимо составить исходную схему расчета показателя:

.

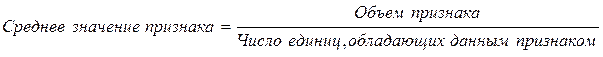Например, 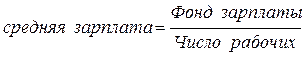; 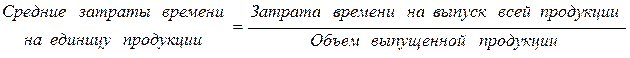. Если в условии задачи известен знаменатель исходной схемы, а неизвестен числитель, то применяется средняя арифметическая взвешенная. Если известен числитель, а знаменатель – нет, то используется средняя гармоническая взвешенная.

Средняя квадратическая применяется в тех случаях, когда варианты представляют собой отклонение заданных величин от нормы, от ГОСТа, от стандарта, т.е. от какой-то постоянной величины, в том числе и от среднего значения.

Рассчитывается: 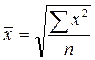- простая; 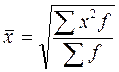- взвешенная;

где f – количество единиц совокупности с тем или иным отклонением; х – отклонения (±)

Для характеристики структуры совокупности применяются особые показатели, которые называют структурными средними. Это мода и медиана. Эти показатели будут рассмотрены в теме 5.

Тесты