Плотность заряда и её вид в случае системы точечных зарядов
Электродинамика сплошных сред
(конспект лекций для ЭКТ-37)
Г.
Оглавление
1 §1. Плотность заряда и её вид в случае системы точечных зарядов. 4
2 §2. Уравнения Максвелла для электромагнитного поля в вакууме. 4
3 §3. Закон сохранения заряда в форме уравнения непрерывности. 5
4 §4. Теорема Остроградского-Гаусса. 6
5 §5. Потенциалы электромагнитного поля в вакууме. 6
6 §6. Градиентная инвариантность. 6
7 §7. Типы калибровок. 7
8 §8. Микро и Макро уравнения Максвелла для электромагнитного поля в среде. 9
§9. Материальные уравнения или уравнения связи. 11
* §10. Тензоры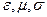 
и их свойства. 12
§11. Потенциалы электромагнитного поля в среде. 13
§12. Калибровка Лоренца в случае однородной изотропной среды. 13
9 §13. Уравнение Даламбера(без учёта пространственной дисперсии). 14
* §14. Поведение электромагнитного поля при переходе через границу раздела двух сред. 15
10 §15. Уравнения Максвелла для стационарного электромагнитного поля в среде. 18
11 §16. Уравнения Пуассона в электростатике. 19
§17. Краевые, граничные условия. Задачи Дирихле и Неймана. 20
§18. Функция Грина задач электростатики. 20
§19. Физический смысл функции Грина. 21
§20. Теорема взаимности в электростатике. 22
§21. Функция Грина в случае неограниченной области. 22
§22. Оператор трансляции. 23
§23. Потенциал системы зарядов. 24
12 §24. Электрические (дипольный и квадрупольный) моменты. 25
§25. Электрическое поле системы зарядов на больших расстояниях. 26
§26. Поверхностная плотность зарядов на границе раздела двух поляризованных диэлектриков. 28
* §27. Электрический дипольный момент поляризованного диэлектрика. Роль поверхностных зарядов. 29
* §28. Электрическое поле поляризованного диэлектрика. Поле диполя. 30
* §29. Случай однородно-поляризованного диэлектрика. 31
* §30. Задача о расчёте поля внутри эллипсоидальной полости в однородно-поляризованном диэлектрике. 32
§31. Система зарядов во внешнем электростатическом поле. 33
* §32. Энергия взаимодействия двух электрических мульти-полей. 34
13 §33. Векторный потенциал системы стационарных токов. 35
14 §34. Магнитный дипольный момент системы токов. 36
15 §35. Приближение линейного тока. 37
16 §36. Уравнения Максвелла для квазистационарного электромагнитного поля. 37
§37. Условия квазистационарности поля. 39
17 §38. Глубина проникновения квазистационарного электромагнитного поля. 39
18 §39. Уравнения Максвелла электромагнитных волн в вакууме. 41
19 §40. Волновое уравнение в случае вакуума. 41
§41. Решение волнового уравнения в случае плоской электромагнитной волны в вакууме. 41
20 §42. Плоская монохроматическая волна. 44
21 §43. Уравнения Максвелла в случае плоской монохроматической волны в вакууме. 44
§44. Разложение электромагнитных полей по плоским монохроматическим волнам. 45
§45. Теорема Пойнтинга(Закон сохранения энергии электромагнитных волн в форме уравнения непрерывности). 45
22 §46. Соотношение между векторами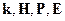 
в случае плоских электромагнитных волн в вакууме. 46
§47. Функция Грина уравнения Гельмгольца. 48
§48. Запаздывающая функция Грина уравнения Даламбера. 49
* §49. Теорема Пойнтинга с учётом диссипации для среды. 51
§50. Пространственно-временная дисперсия в электродинамике. 51
* §51. Уравнения Максвелла для электромагнитного поля в среде с пространственно-временной дисперсией. 53
§52. Волновое уравнение в случае среды с пространственной дисперсией. 53
(*) §53. Дисперсионное уравнение. 54
§54. Нормальные электромагнитные волны в неограниченной среде. 55
§55. Поперечные и продольные нормальные волны в среде. 55
* §56. Решение дисперсионного уравнения в случае однородной и изотропной среды с пространственной дисперсией. 56
§57. Групповая скорость. 57
23 §58. Плазма. Определение и свойства. 59
§59. Метод самосогласования. 59
§60. Использование метода самосогласования для нахождения электростатического потенциала в плазме. 60
24 §61. Дебаевский радиус экранирования. 61
§62. Малые колебания в плазме. 62
§63. Запаздывающие потенциалы. 63
25 §64. Разложение запаздывающих потенциалов в ряды по малому параметру. 63
§65. Калибровка Лоренца в случае запаздывающих потенциалов. 64
26 §66. Дипольное излучение. 66
27 §67. Волновая зона дипольного излучения. 66
28 §68. Ближняя зона дипольного излучения. 68
29 §69. Интенсивность дипольного излучения в волновой зоне. 70
§70. Теорема взаимности в теории излучения. 71
___Задачи по курсу «Электродинамика сплошных сред». 71
__ Задачи по курсу «Электродинамика сплошных сред» и их решения. 79
Список литературы. 89
Плотность заряда и её вид в случае системы точечных зарядов.
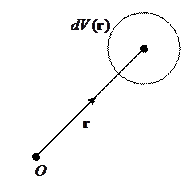
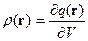
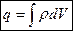
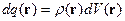
Рассмотрим систему из точеченого заряда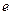 
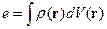
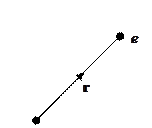Здесь возникает необходимость использовать 
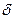-функцию.
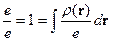
Тогда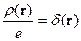 
.
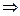
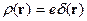Это соответствует случаю, когда заряд помещён в начало координат, а плотность заряда ищется в точке, с радиус-вектором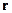 
.
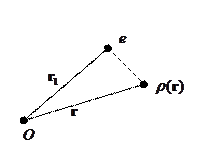
Если же заряд помещён не в начало отсчёта, то плотность заряда перепишется в следующем виде:
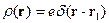
В случае системы точечных зарядов имеем:
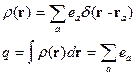
Нужно отметить, что всегда для изображения плотности точечного источника используется 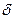-функция.