Автокорреляция регрессионных остатков. Методы выявления

Регрессионная модель МНК позволяет получить несмещенную оценку с минимальной дисперсией только тогда, когда остатки независимы друг от друга. Нарушение условия независимости остатков ( 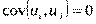) называется автокорреляцией. Если имеет место автокорреляция остатков, то коэффициенты регрессии не смещены, но стандартные ошибки недооценены, а проверка статистической значимости коэффициентов ненадежна. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих наблюдений. Автокорреляция остатков обычно встречается в регрессионном анализе при использовании данных временных рядов. В силу этого в дальнейших выкладках вместо символа i порядкового номера наблюдения будем использовать символ t, отражающий момент наблюдения. Объем выборки при этом будем обозначать T.

Причины автокорреляции:

- ошибки спецификации – неучет в модели важной объясняющей переменной или неправильный выбор формы зависимости;

- эффект паутины – многие экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом).

Методы обнаружения автокорреляции

В силу неизвестности значений параметров уравнения регрессии неизвестными будут также и истинные значения отклонений 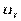,t= 1, 2, ..., Т. Поэтому выводы об их независимости осуществляются на основе оценок ε_t,t= 1, 2, ..., Т, полученных из эмпирического уравнения регрессии. Рассмотрим возможные методы определения автокорреляции.

Метод рядов.

Последовательно определяются знаки отклонений 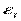,t= 1, 2, ..., Т.

Например, (- - - - -)(+++++++)(- - -)(++++)(-),

т.е. 5 «-», 7 «+», 3 «-», 4 «+», 1 «-».

Ряд определяется как непрерывная последовательность одинаковых знаков. Количество знаков в ряду называетсядлиной ряда.

Визуальное распределение знаков свидетельствует о неслучайном характере связей между отклонениями. Если рядов слишком мало по сравнению с количеством наблюдений п, то вполне вероятна положительная автокорреляция. (В большинстве случаев положительная автокорреляция вызывается направленным постоянным воздействием некоторых неучтенных в модели факторов). Если же рядов слишком много, то вероятна отрицательная автокорреляция. Для более детального анализа предлагается следующая процедура. Пусть

п— объем выборки;

п₁— общее количество знаков «+» прип наблюдениях;

п₂— общее количество знаков «—» прип наблюдениях ; .

k— количество рядов.

Если при достаточно большом количестве наблюдений (n₁>10,п₂>10) количество рядовkлежит в пределах

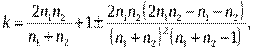
то гипотеза об отсутствии автокорреляции не отклоняется.

Для небольшого числа наблюдений (n₁<20,n₂<20) Свед и Эйзенхарт разработали таблицы критических значенийk₁,k₂отn₁,n₂.

Если 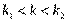, то говорят об отсутствии автокорреляции;

если 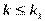, говорят о положительной автокорреляции остатков;

если 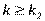, говорят об отрицательной автокорреляции остатков.

В нашем примере: n=20,n₁=11,n₂=9,k=5. По таблицамk₁=6,k₂=16. Пронимается предположение о наличии положительной автокорреляции на уровне значимости 0,05.

Для проверки автокорреляции первого порядка (для регрессии временных рядов) необходимо рассчитать критерий Дарбина—Уотсона. Он определяется так:

.

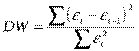Эмпирическое правило гласит, что если критерий Дарбина- Уотсона равен двум, то не существует положительной автокорреляции, если он равен нулю, то имеет место совершенная положительная автокорреляция, а если он равен четырем, то имеет место совершенная отрицательная автокорреляция. Критерий Дарбина—Уотсона имеет выборочное распределение, которое обладает двумя критическими значениями: d_L – нижняя границаиd_U– верхняя граница.

Если 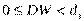, то существует положительная автокорреляция;

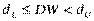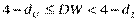, - вывод о наличии автокорреляции не определен;

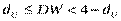- нет автокорреляции;

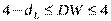- существует отрицательная автокорреляция.