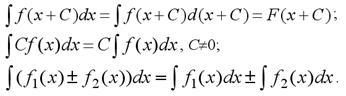Провести повне дослідження і побудоувати графік функції

y =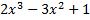

1.Шукаємо область визначення функції:

x є ( )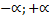

2.Досліджуємо функцію на парність чи не парність

y (+x)=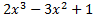

y (-x)=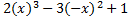

y(-x)=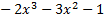

y(-x)=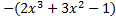

y (+x) парна якщо точка повністю така сама

y (+x) не парна якщо «-» виходить за дужки

Функція не є парною,і не є непарною.

3.Досліджуємо функцію на неперервність

Функція неперервна(бо x є ( ))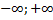

(Якщо є (5; 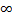) – функція неперервна але існує точка розриву)

4.Шукаємо асимптоти:

1.Вертикальна(буде тоді коли в пункті 3 буде точка розриву) – графік неможе проходити

2.Горизонтальна -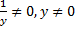

Вертикальних і горизонтальних асимптот немає.

3.Похила

Шукається за правилом:

k = 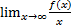якщо число є то те число залишається,а якщо 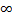то її немає!

k = =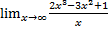

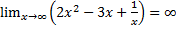
Похилої асимптоти немає.

5.Шукаємо точки максимуму і мінімуму.

Для цього знаходимо першу похідну:

=

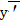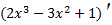
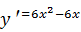
Прирівнюємо похідну до нуля

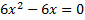
6x(x-1)=0

6x=0 або x-1=0

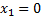
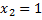
Критичні точки першого роду підозрілі на екстремуми

Підставляємо будь які точки в похідну і звертаємо увагу на знак.

+ - +

0 1

Max min

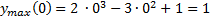
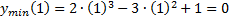
6.Шукаємо інтервали опуклості і увігнутості графіка функціх,точки перегину

Для цього обчислюємо другу похідну

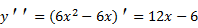
Прирівнюємо до 0.

12x-6=0

12x=6

X=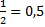

Критична точка другого роду,яка підозріла на точку перегину

Е

- +

12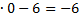

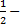точка перегину

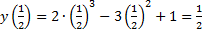
7.

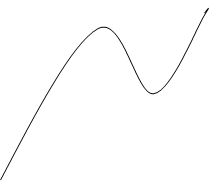
Max

(

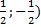
Min

3.Асимптоти,область визначення функції та монотонні функції.

Асимптоти функції

Визначення асимптот функції не таке і важке заняття, якщо Ви знаєте ряд правил та маєте добрі знання з обчислення границь. Якщо ж не вмієте шукати границі, то надолужувати доведеться багато, проте навчитися можна.

Пряма називається асимптотою кривої, якщо точка кривої необмежено наближається до неї при зростанні абсциси чи ординати. Асимптоти поділяють на вертикальні, похилі (горизонтальні) асимптоти.

ВЕРТИКАЛЬНІ АСИМПТОТИ

Графік функції 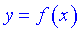при x 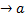має вертикальну асимптоту, якщо границя функції нескінченна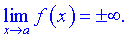

Крім цьому точка x=a є точкою розриву II роду, а рівняння вертикальної асимптоти має вигляд x = a.

ПОХИЛІ АСИМПТОТИ

Рівняння похилої асимптоти має вигляд 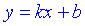де k, b - границі, що обчислюються за правилом

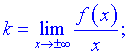
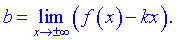
Якщо обидві границі існують і скінченні то функція має похилу асимптоту, інакше – не має. Слід окремо розглядати випадки, коли 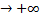x та x .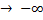

ГОРИЗОНТАЛЬНІ АСИМПТОТИ

Крива 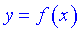має горизонтальну асимптоту y= C тільки в тому випадку, коли існує скінченна границя функції при 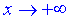та 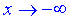, і ця границя рівна 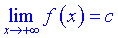або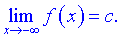

Область визначення функції

Областю визначення називають множину значень аргументу x при яких існує значення 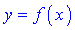і позначають D(y) або D(f). Областю значень називають множину чисел, які приймає функція 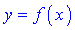при проходженні аргументом x всіх визначених значень. Її позначають E(y) або E(f) . Графічно обидві множини добре ілюструє наступний рисунок

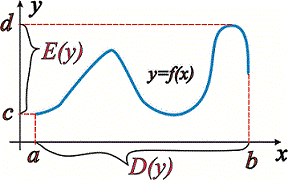
Для схематичної функції розглядувані області приймають значення

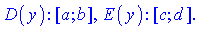
Методика знаходження області визначення для всіх функцій одна і та ж: потрібно виявити точки при яких функція не існує, а потім виключити їх з множини дійсних чисел 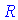. В результати отримаємо набір проміжків чи інтервалів, точки, які і утворюють область визначення.

Інтервали монотонності функції. Критичні точки

Дослідження функцій повинно починатися з встановлення області визначення та інтервалів монотонності. Для цього студент повинен володіти добрими знаннями поведінки елементарних функцій та наступним теоретичним матеріалом.

Функція y=f(x) називається зростаючою на інтервалі (a;b) , якщо для будь-яких двох точок 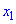і 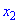з цього проміжку, і таких, що 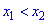, виконується нерівність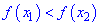

Для того щоб функція y=f(x) була спадною на інтервалі (a;b) необхідно, щоб для будь-яких 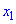і 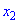, що належать до цього інтервалу, і відповідають умові 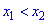, справджувалася нерівність .

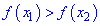Як зростаючі, так і спадні функції називаються монотонними, а інтервали, в яких функція зростає або спадає – інтервалами монотонності.

Область зростання і спадання функції y=f(x) характеризується знаком її похідної: якщо у деякому інтервалі 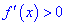, то функція зростає в цьому інтервалі;

якщо ж 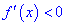– то функція спадає в цьому інтервалі.

Інтервали монотонності можуть прилягати один до одного або точками, де похідна дорівнює нулю або точками, де похідна не існує. Ці точки називаються критичними точками.

Для того, щоб знайти інтервали монотонності функції y=f(x) потрібно:

1) знайти область визначення функції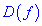

2) обчислити похідну даної функції;

3) знайти критичні точки з рівняння 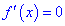та за умови, що 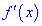не існує;

4) розділити критичними точками область визначення на інтервали і у кожному з них визначити знак похідної.

На інтервалах де похідна додатна, функція зростає, а де від'ємна – спадає.

4.Дослідження функції на парність і непарність

Щоб дослідити функцію y=f(x) та побудувати її графік необхідно:

1) знайти область визначення функції, тобто множину всіх точок для яких існує значення функції;

2) знайти (якщо вони існують) точки перетину графіка з координатними осями. Для цього потрібно у рівняння y=f(x) підставити x=0 , а також розв'язати рівняння f(x)=0 для відшукання точок перетину з віссю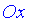

3) дослідити функцію на періодичність, парність і непарність. У деяких випадках це можна зробити візуально за самим виглядом функції, якщо ні- то проводимо перевірку:

1. 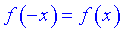– функція парна;

2. 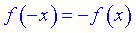– функція непарна;

3. 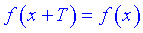– функція періодична, T – період функції.

Tаким чином, якщо маємо парну функцію y=f(x) , то достатньо побудувати її для додатніх значень x 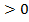, після чого відобразити симетрично відносно осі абсцис y на решту області. У випадку непарної функції графік буде симетричний відносно початку координат. Для прикладу, якщомаємо непарну функцію, графік якої належить першій чверті другу половину отримаємо поворотом першої чверті на 180 градусів (третя чверть).

Періодичними є переважно фукнкції, складені з простих тригонометричних та деякі параметрично задані функції.

1) знайти точки розриву та дослідити їх (такими точками є краї інтервалів визначення функції);

2) знайти інтервали монотонності, точки екстремумів та значення функції в цих точках;

3) знайти інтервали опуклості, вгнутості та точки перегину;

4) знайти асимптоти кривої;

5) побудувати графік функції.

5. Похідні основних елементарних функцій

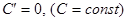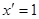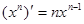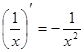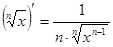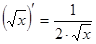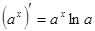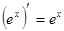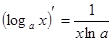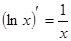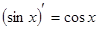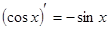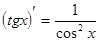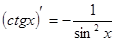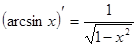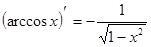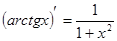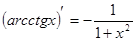Тема 9:Невизначений інтеграл

1.Первісна функція

Означення. Функція F(x) на заданому проміжку називається первісною для функції f(x), для всіх x з цього проміжку, якщо F'(x)=f(x).

Операція знаходження первісної для функції називається інтегруванням. Вона є оберненою до операції диференціювання.

Теорема. Всяка неперервна на проміжку функція (x) має первісну на цьому проміжку.

Теорема (основна властивість первісної). Якщо на деякому проміжку функція F(x) є первісною для функції f(x), то на цьому проміжку первісною для f(x) буде також функція F(x)+C, де C довільна стала.

З цієї теореми випливає, що коли f(x) має на заданому проміжку первісну функцію F(x), то цих первісних безліч. Надаючи C довільних числових значень, кожного разу діставатимемо первісну функцію.

Для знаходження первісних користуються таблицею первісних. Вона отримується із таблиці похідних.

2.Невизначений інтеграл

Означення. Множина всіх первісних функцій для функції f(x) називається невизначеним інтегралом і позначається 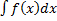або F(x)+C

При цьому f(x) називається підінтегральною функцією, а f(x)dx - підінтегральним виразом.

Отже, якщо F(x), є первісною для f(x), то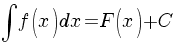

3.Властивості ,методи інтегрування.

Властивості невизначеного інтегралу