Параметрическое уравнение прямой

Пусть l задана каноническим уравнением: 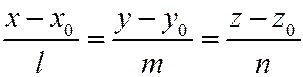. Обозначим равенство трех отношений через t. Преобразовав уравнение, получим:

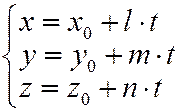- параметрическое уравнение прямой(11.3)

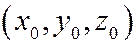- координаты начальной точки ;

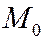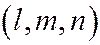- координаты направляющего вектора, t – параметр.

Параметрическое уравнение прямой удобно применять в задачах на нахождение точки пересечения прямой и плоскости.

Пример 11.2. Найти точку пересечения прямой l и плоскости a. , .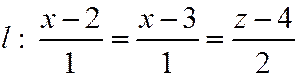

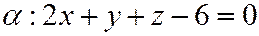Запишем уравнение прямой в параметрическом виде: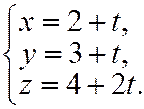

Подставим эти значения 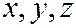в уравнение плоскости: ,

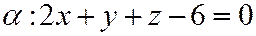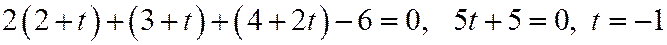- параметр определили и подставим его в систему: 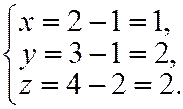Искомая точка .

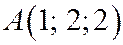Уравнение прямой, проходящей через две точки в пространстве

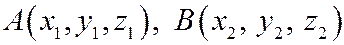-две точки пространства. По аналогии с прямой на плоскости:

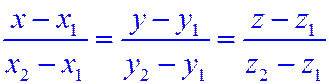(11.4)

Угол между двумя прямыми в пространстве

Пусть заданы прямые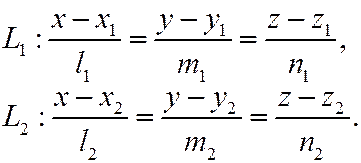

Тогда угол определяется по формуле: .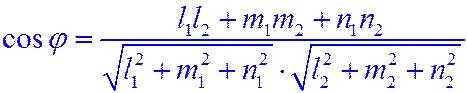

Условия параллельности и перпендикулярности двух прямых в пространстве

Пусть две прямые заданы каноническим видом. Их направляющие векторы: .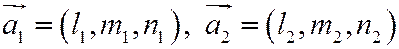

Теорема 11.1: Две прямые параллельны тогда и только тогда, когда 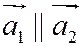т.е. .

Те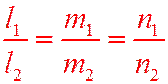орема 11.2: Две прямые перпендикулярны тогда и только тогда, когда 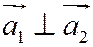, т.е. 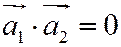, т.е. .

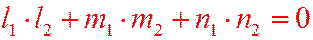Угол между прямой и плоскостью. Параллельность прямой и плоскости, перпендикулярность прямой и плоскости

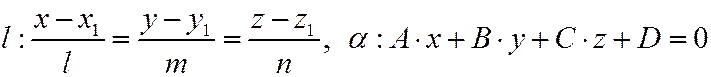
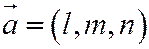- направляющий вектор, 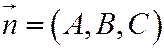- нормаль к плоскости.

Угол между прямой и плоскостью определяется по формуле:

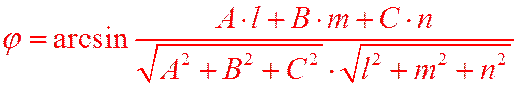
Условие параллельности прямой и плоскости в пространстве:

.

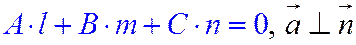Условие перпендикулярности прямой и плоскости в пространстве:

.

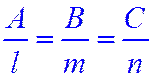Поверхности второго порядка

Поверхности являются пространственными аналогами кривых второго порядка на плоскости.

Эллипсоид

Определение. Эллипсоидом называется поверхность, которая в некоторой декартовой системе координат определяется уравнением:

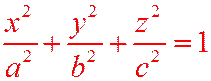- каноническое уравнение эллипсоида. (12.1)

Рассмотрим форму эллипсоида с помощью «метода параллельных сечений». Рассмотрим сечения данного эллипсоида плоскостями, параллельными Оху, т.е. z=h. Линия, которая получается в сечении, определяется двумя уравнениями:

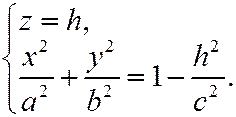(12.2)

Если:

1) 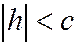, то плоскость z=h пересекает эллипсоид (12.1) по эллипсу с полуосями: .

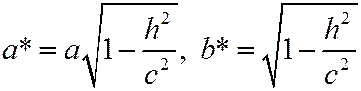2) Величины 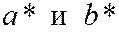имеют наибольшие значения при h=0, иначе говоря, самый крупный эллипсоид получается при сечении координатной плоскостью z=0.

3) При возрастании 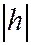величины 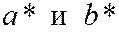уменьшаются.

4) При 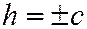величины 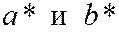обращаются в 0, т.е. сечение эллипса вырождается в точку .

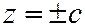5) При 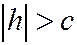, уравнения (12.2) определяют мнимый эллипс, т.е. плоскость z=h с данным эллипсоидом не встречается совсем.

Совершенно аналогично рассматриваются сечения эллипсоида плоскостями, параллельными .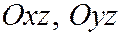

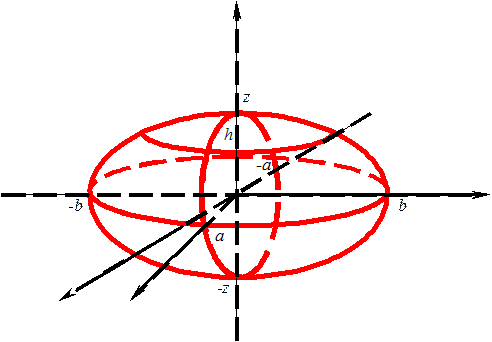Таким образом, вывод: эллипсоид есть замкнутая овальная поверхность, обладающая тремя взаимно перпендикулярными плоскостями симметрии. Величины 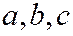называются полуосями эллипсоида. Если все они различны, то эллипсоид называется трехостным.

При 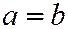эллипсоид, можно рассмотреть как поверхность, образованную вращением эллипса вокруг одной из его осей: если эллипсоид образован вращением вокруг его большой оси, он называется вытянутым эллипсоидом вращения, если вокруг меньшей оси – то сжатым эллипсоидом вращения.

В случае 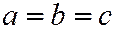имеем сферу.

Уравнение 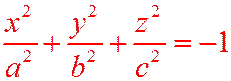, ввиду аналогии с (12.1) называется уравнением мнимого эллипсоида: 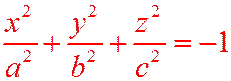(12.3)

Гиперболоид

Определение.Однополостным гиперболоидом называется поверхность, которая в данной декартовой системе координат определяется уравнением: 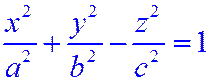(12.4)

Определение.Двухполостным гиперболоидом называется поверхность, определяемая уравнением: 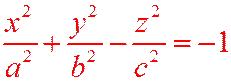(12.5)

Однополостный гиперболоид

Он задается уравнением (12.4). Рассмотрим сечение его координатными плоскостями .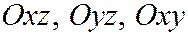

Сечение плоскостью 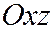(у=0) определяется уравнениями: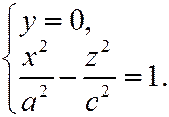

Мы видим, что эта гипербола расположена симметрично относительно осей Ox и Oz и пересекает ось Ox в точках .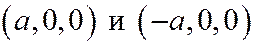

Сечение плоскостью 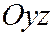(х=0) определяется уравнениями:

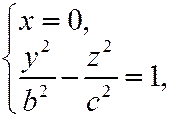- это гипербола, симметричная относительно осей Ox и Oz и пересекает ось 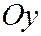в точках .

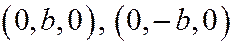Сечение плоскостью 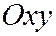(z=0) определяется уравнениями:

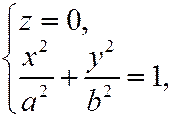- эллипс, который лежит в плоскости 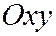. Он называется горловым.

Рассмотрим произвольное сечение плоскостью z=h, параллельной Оху:

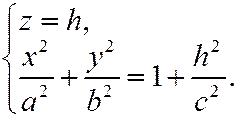
1) Плоскость z=h пересекает гиперболоид (12.4) по эллипсу с полуосями .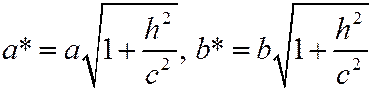

2) Величина 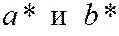имеют наименьшие значения при h=0, т.е. сечение плоскостью z=0.

3) При возрастании 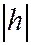величины 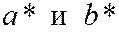бесконечно возрастают.

Построим однополостный гиперболоид:

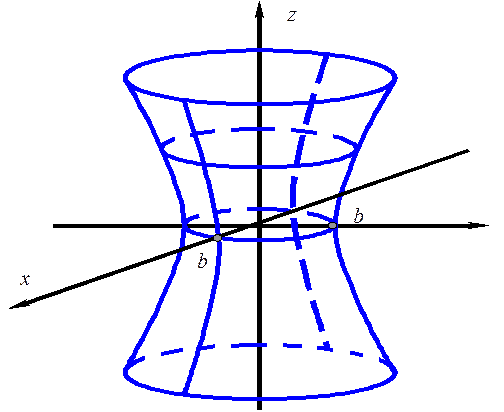Вывод: однополостный гиперболоид имеет вид бесконечной трубки, бесконечно расширяющейся в обе стороны от горлового эллипса.

Величины 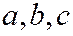называют полуосями однополостного гиперболоида. Полуось с в уравнении (12.4) стоит со знаком «минус», значит, вокруг этой оси происходит вращение гиперболы.

Замечание: В уравнении (12.4) знак «минус» может стоять и при 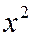, и при 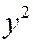, тогда трубка однополостного гиперболоида будет располагаться вокруг ос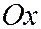и или .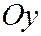

Двухполостный гиперболоид

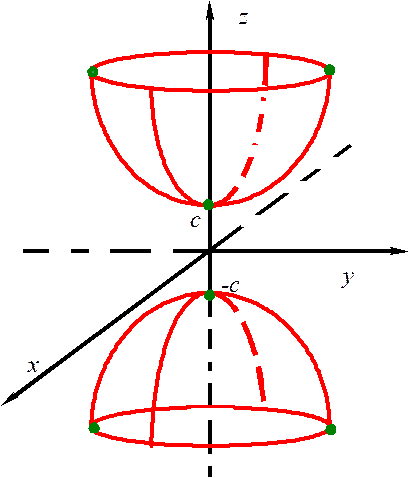Задаётся уравнением:

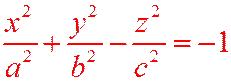(12.5)

Рассмотрим сечение плоскостью .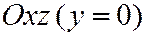

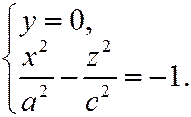-гипербола симметрична осям 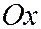и 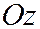, и ось 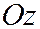пересекает в точках 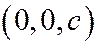и .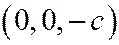

Сечение плоскостью .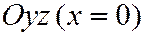

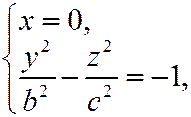- это гипербола, симметричная относительно осей Oу и Oz и пересекает ось 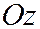в точках 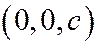и .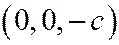

Сечение плоскостью z=h.

(*)

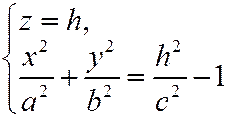
1) 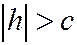, то плоскость пересекает двухполостный гиперболоид по эллипсу с полуосями 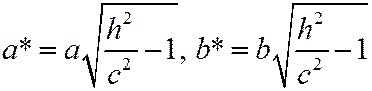,симметричному 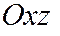и .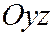

2) При возрастании 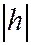величины 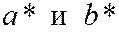возрастают.

3) При убывании 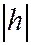величины 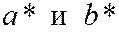убывают и приближаются к нулю при 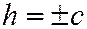, имеем 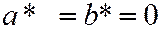Þ эллипс вырождается в точку.

4) При 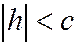, система (*) определяют мнимый эллипс, т.е. плоскость z=h с данным гиперболоидом не встречается совсем.

Вывод: Двухполостный гиперболоид есть поверхность, состоящая из двух полостей, каждая имеет вид бесконечной выпуклой чаши, он обладает тремя взаимно перпендикулярными плоскостями симметрии.

Величины 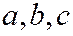называется полуосями двухполостного гиперболоида. Двухполостный гиперболоид можно рассматривать как поверхность, образованную вращением гиперболы вокруг из осей, а именно той, которая гиперболу пересекает.

Параболоид

Эллиптический параболоид

Определение. Эллиптическим параболоидом называется поверхность, которая в декартовой системе координат определяется уравнением:

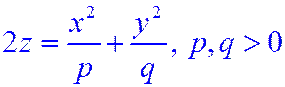(12.6)

Исследуем эту поверхность методом сечений:

Сечение плоскостью :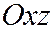

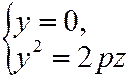- парабола, симметричная относительно оси 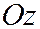, с вершиной в точке 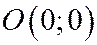.Сечение плоскостью :

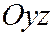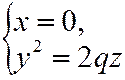- парабола, симметричная оси .

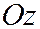Теперь рассмотрим сечение плоскостью, параллельной .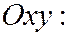

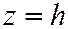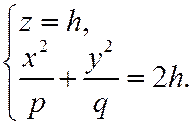
1) При 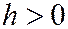плоскость 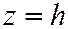пересекает эллиптический параболоид по эллипсу с полуосями .

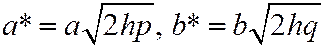2) При возрастании 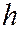величины 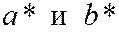возрастают.

3) При убывании 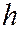величины 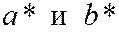убывают. При 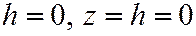вырождается в точку .

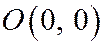4) При 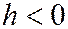, будем иметь мнимый эллипс, т.е. плоскость z=h с параболоидом не встречается совсем.

Вывод: Эллиптический параболоид имеет вид выпуклой чаши. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка О называется вершиной эллиптического параболоида. Числа 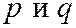называются его параметрами.

Эллиптический параболоид можно рассматривать как вращение параболы вокруг оси z.