Задачі на взаємне розміщення прямої та площини

Задача 35.1.Скласти рівняння площини, що проходить через точку 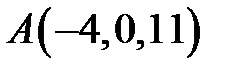перпендикулярно прямій .

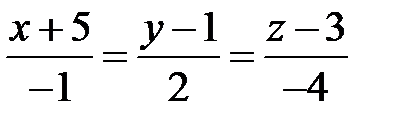Розв’язання.

З умови перпендикулярності прямої і площини випливає, що за нормальний вектор площини можна взяти напрямний вектор прямої: .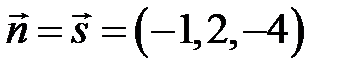

Тоді рівняння площини має вигляд:

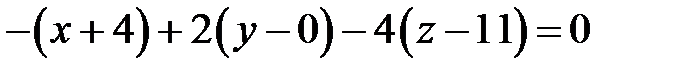, або .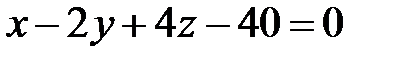

Задача 35.2.Знайти кут між прямою 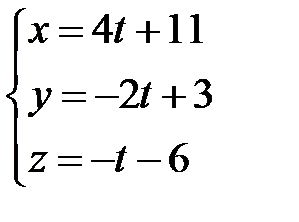та площиною .

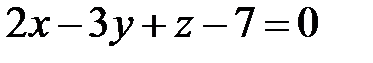Розв’язання.

З даних рівнянь 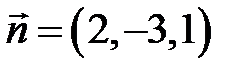, 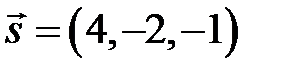. Згідно формули маємо:

.

Задача 35.3. Знайти точку перетину прямої 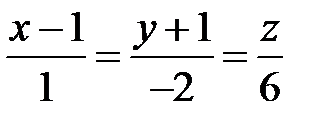та площини .

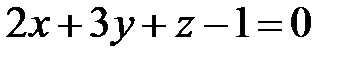Розв’язання.

Подамо рівняння прямої в параметричному вигляді: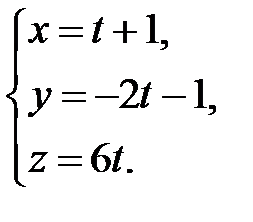

Підставимо одержані вирази в рівняння площини, щоб знайти значення параметра 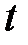, яке відповідає точці перетину прямої та площини.

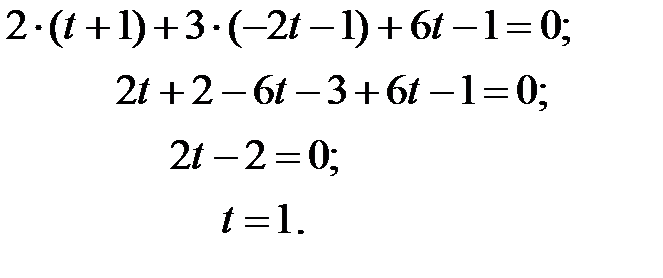
Тепер знайдемо координати точки перетину М:

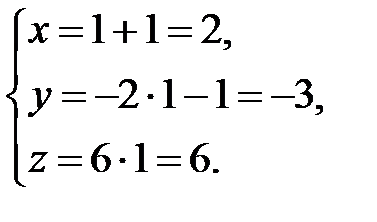
Отже, точка перетину .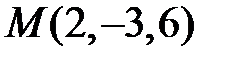

Задача 35.4.Показати, що пряма 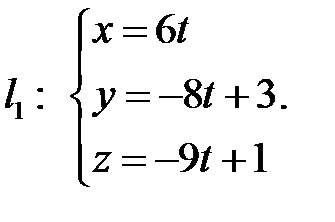паралельна площині 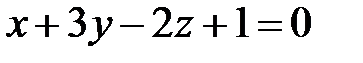, а пряма 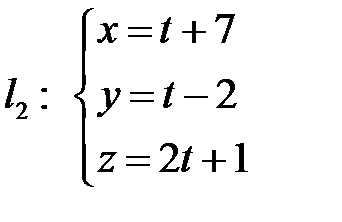лежить в цій площині.