Фрагмент решения задачи 2.1

ЛАБОРАТОРНАЯ РАБОТА № 2.

РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Цель: сформировать навыки решения нелинейных уравнений численными методами.

Отчетпо лабораторной работе должен содержать следующие материалы по каждой задаче:

1) постановка задачи;

2) необходимый теоретический материал;

3) результаты вычислительного эксперимента;

4) анализ полученных результатов;

5) графический материал (если необходимо);

6) тексты программ.

Варианты заданий к задачам 2.1-2.10 даны в ПРИЛОЖЕНИИ 2.A.

Основные теоретические сведения

1.1.Пусть задана непрерывная функция f(x) и требуется найти корни уравнения

f(x)=0 (1)

на всей числовой оси или на некотором интервале .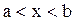

Всякое значение 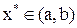, удовлетворяющее условию 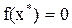, называется корнем уравнения (1), а способ нахождения этого значения 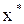- решением уравнения (1).

Численное решение уравнения проводится в два этапа:

1 этап. Отделение корней уравнения.

2 этап. Уточнение интересующих корней с заданной точностью ε.

Отделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a,b], которому он принадлежит.

Уточнение корня – это вычисление интересующего корня с заданной точностью e.

Расчетные формулы методов решения нелинейного уравнения .

Метод дихотомии (половинного деления, бисекций):

x = (a+b)/2 , если ¦(a) ·¦(x)>0 => x^*Î [x,b] => a=x, иначе x^*Î [a, x] => b=x

Оценка количества итераций n, требуемых для достижения требуемой точности ε (на заданном отрезке [a,b]):

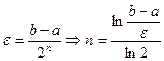
Условие завершения вычислений : длина отрезка не превышает заданную точность и значение функции близко к 0 с заданной точностью:

b-a ≤ ε ∩ |¦(x)| ≤ ε.

Метод простых итераций (метод последовательных приближений).

x_i=φ(x_i-1) , i=1,2,… где i − номер итерации

Условие сходимости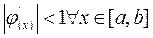

Условие завершения итерационного процесса:

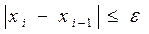
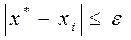
Упрощенный метод Ньютона: 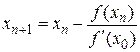, n=0,1,…

Условие окончания расчета:

,

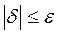где 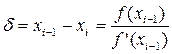−корректирующее приращение или поправка.

Условие сходимости итерационного процесса:

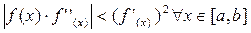
Метод ложного положения: 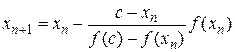, n=0,1,…;

c-фиксированная точка из окрестности корня

Метод секущих: 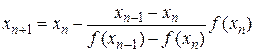, n=0,1,…

Метод Стеффенсена: 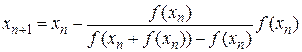, n=0,1,…

Модифицированный метод Ньютона для поиска кратных корней:

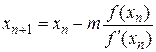, n=0,1,…, m=1,2,…

Индивидуальные задания

Задача 2.1. Даны два уравнения f(x)=0 и g(x)=0. Найти с точностью 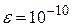все корни уравнений, содержащиеся на отрезке [a, b]. Для решения задачи использовать метод бисекции.

ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:

1. Найти аналитическое решение уравнения f(x)=0.

2. Локализовать корни f(x)=0 графически.

3. Найти корни уравнения f(x)=0 с точностью 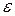с помощью метода бисекции.

4. Найти корни уравнения f(x)=0 с точностью .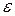

5. Аналогично п. 1-4 попытаться найти корни уравнения g(x)=0. Объяснить полученные результаты.

Фрагмент решения задачи 2.1.

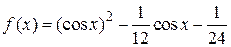=0, [a,b]=[0,]

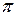Аналитическое решение задачи:

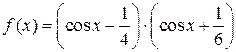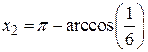, =1.31811607652818, =1.738244406014586

Численное решение задачи: Локализация корней для численного решения задачи:

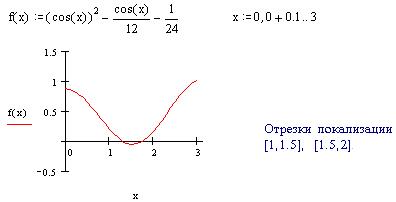
Метод бисекции

(на примере работы пакета MATHCAD)

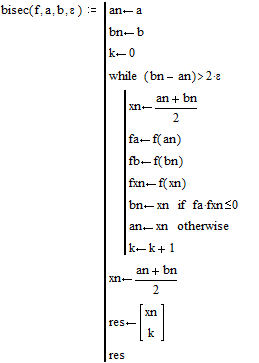
ПЕРВЫЙ КОРЕНЬ

bisec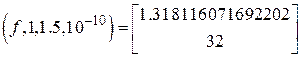

Встроенная функция пакета MATHCAD

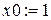- задание начального приближения

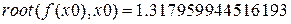
Значение корня отличается от найденного с помощью функции bisec , так как по умолчанию величина погрешности при работе встроенных функций равна 0.001.

Переопределим параметр для задания погрешности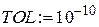

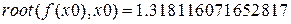
Значение корня с заданной точностью 1.3181160717.

ВТОРОЙ КОРЕНЬ

bisec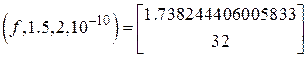

Значение корня с заданной точностью 1.7382444060, число итераций 32.

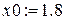- задание начального приближения

.

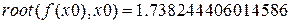Значения корней в пределах заданной точности совпадают.

Задача 2.2.Найти указанный в варианте корень уравнения f(x)=0 с точностью 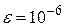, двумя способами.

а) Использовать метод бисекции. Предварительно определить отрезок локализации [a, b].

b) Использовать метод Ньютона. В качестве начального приближения для метода Ньютона взять середину отрезка локализации из п. а).

Сравнить число итераций в п. a), b).

Задача 2.3.Локализовать корни уравнения f(x)=0 и найти их с точностью 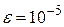, используя метод простой итерации. К виду x=j(x), удобному для итераций, уравнение f(x)=0 привести двумя способами.

a) Преобразовать уравнение к виду x=x-af(x), где a=2/(M+m), 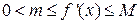, а x принадлежит отрезку локализации [a, b].

b) Любым другим преобразованием уравнения. Проверить достаточное условие сходимости метода.

Использовать критерий окончания итерационного процесса вида 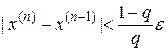, где в п. a) q=(M-m)/(M+m), в п. b) .

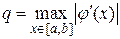Сравнить число итераций и значения величины q в п. a), b).

Задача 2.4.Локализовать корни уравнения f(x)=0. Найти их с точностью 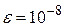, используя методы простой итерации и Ньютона. Сравнить скорость сходимости методов (по числу итераций).

Задача 2.5.Найти приближенно корень уравнения f(x)=0, принадлежащий отрезку [a,b], с точностью 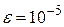, используя модификацию метода Ньютона для случая кратного корня при значениях m=1,2,3,4,5. По числу итераций определить кратность корня.

Задача 2.6.(ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ)

Локализовать корни уравнения f(x)=0. Найти их с точностью 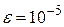и 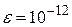, используя метод Ньютона и метод, указанный в индивидуальном варианте. Сравнить скорость сходимости методов (по числу итераций) для каждого значения .

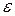Задача 2.7.Локализовать корни уравнения f(x)=0. Найти их с точностью 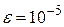и 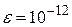, используя метод Ньютона, упрощенный метод Ньютона и метод секущих. Сравнить скорость сходимости методов (по числу итераций) для каждого значения .

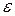Задача 2.8.(ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ)

Найти приближенно все (в том числе комплексные) корни уравнения f(x)=0 с точностью 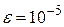, используя метод Ньютона.

УКАЗАНИЕ. Для поиска комплексных корней следует использовать комплексные начальные приближения.

Задача 2.9.(ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ)

a)Локализовать корни уравнения f(x)=0. Уточнить их с точностью 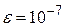, используя метод Ньютона. Для поиска кратного корня и определения его кратности следует использовать модификацию метода Ньютона для случая кратного корня с m=1,2,3. При любых ли начальных приближениях такой метод сходится?

b) Рассмотреть уравнение f(x)+d=0, где 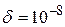. Найти корень кратности 1, используя метод Ньютона. Применить для нахождения кратного корня соответствующую модификацию* метода Ньютона. Удается ли найти кратный корень? Если нет, то использовать метод Ньютона с комплексными начальными приближениями. Сохранился ли кратный корень? Объяснить результаты.

Задача 2.10.(ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ)

Функция y=f(x) задана неявно уравнением F(x,y)=0. На отрезке [1, 5] построить таблицу значений функции y=f(x) с шагом h=0.5, применяя один из методов численного решения нелинейного уравнения (с точностью 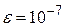). Построить график функции y=f(x) на заданном отрезке.

ПРИЛОЖЕНИЕ 2.A.

ВАРИАНТЫ ЗАДАНИЙ К ЛАБОРАТОРНОЙ РАБОТЕ 2

Таблица к задаче 2.1

N	f(x)	g(x)	[a, b]
2.1.1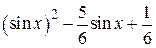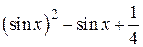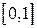
2.1.2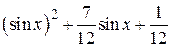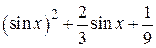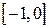
2.1.3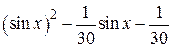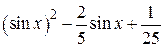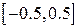
2.1.4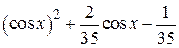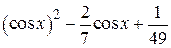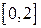
2.1.5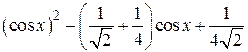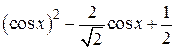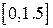
2.1.6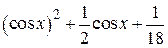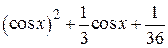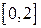
2.1.7.		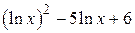	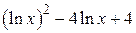[5,25]
2.1.8		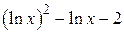	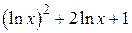[0.1,10]
2.1.9		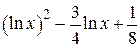	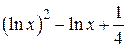[0.1,2]
2.1.10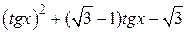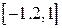
2.1.11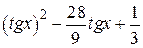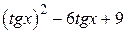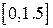
2.1.12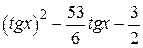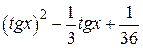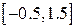
2.1.13		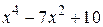	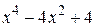[0,3]
2.1.14		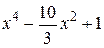	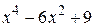[0,2]
2.1.15		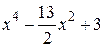	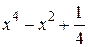[0,3]
2.1.16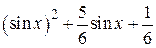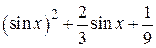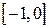
2.1.17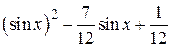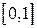
2.1.18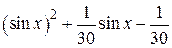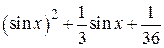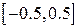
2.1.19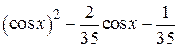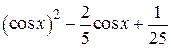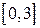
2.1.20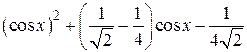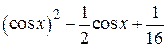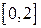
2.1.21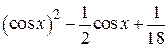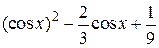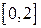
2.1.22		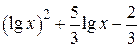	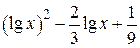[0.001,3]
2.1.23		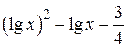	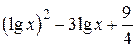[0.1,35]
2.1.24		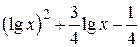	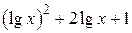[0.01,3]
2.1.25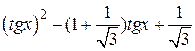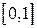
2.1.26		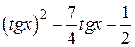	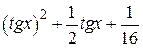[-0.5,1.5]
2.1.27		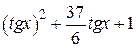	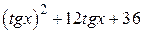[-1.5,0]
2.1.28		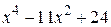	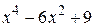[1,3]
2.1.29		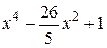	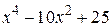[0,3]
2.1.30		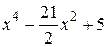	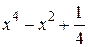[0,5]

Таблица к задаче 2.2 Таблица к задаче 2.3

N	f(x)	Найти корень	N	f(x)
2.2.1		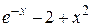отрицательный	2.3.1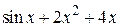
2.2.2		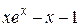положительный	2.3.2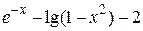
2.2.3		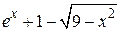положительный	2.3.3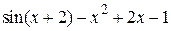
2.2.4		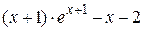наибольший по модулю	2.3.4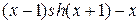
2.2.5		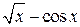все корни	2.3.5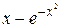

Таблица к задаче 2.4

f(x)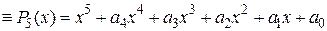
N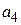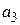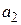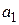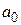
2.4.1	4.545004	-3.055105	-18.06895	4.002429	4.722482
2.4.2	-2.656764	-3.406111	10.89372	-1.752935	-3.423612
2.4.3	-4.556062	2.93309	9.274868	-10.32081	0.422098
2.4.4	7.809249	16.28542	-2.771356	-27.95304	-11.33921
2.4.5	-13.0072	60.24546	-122.0716	105.6798	-30.19201

Таблица к задаче 2.5

N	f(x)	[a, b]
2.5.1		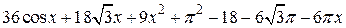[0.8,1.2]
2.5.2		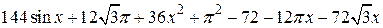[0.3,0.7]
2.5.3		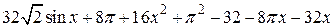[0.5,1]
2.5.4		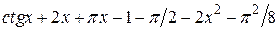[0,1]
2.5.5		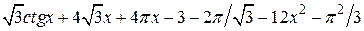[0,0.7]

Таблица к задаче 2.6 Таблица к задаче 2.7

N	f(x)	Метод*	N	f(x)
2.6.1		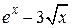упрощенный метод Ньютона	2.7.1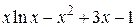
2.6.2		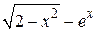метод ложного положения	2.7.2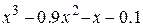
2.6.3		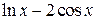метод простой итерации	2.7.3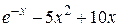
2.6.4		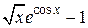метод секущих	2.7.4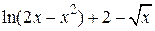
2.6.5		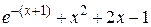метод Стеффенсена	2.7.5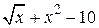

Таблица к задаче 2.8 Таблица к задаче 2.9

N	f(x)	N	f(x)
2.8.1		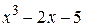2.9.1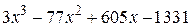
2.8.2		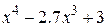2.9.2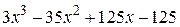
2.8.3		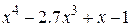2.9.3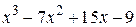
2.8.4		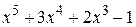2.9.4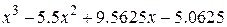
2.8.5		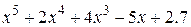2.9.5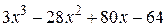

Таблица к задаче 2.10

N	F(x,y)
2.10.1	, ,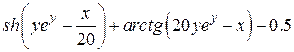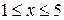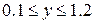
2.10.2	, ,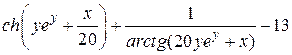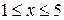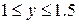
2.10.3	, ,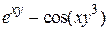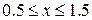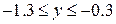
2.10.4	, ,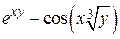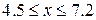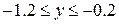
2.10.5	, ,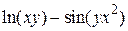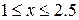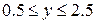

Контрольные вопросы

1. Опишите этапы численного решения уравнений

2. Опишите схему алгоритма отделения корней

3. Перечислите алгоритмы уточнения корней уравнения

4. Опишите методы уточнения корней уравнения

5. Опишите схему алгоритма метода бисекций (дихотомии)

6. Как рассчитать количество итераций n, требуемых для достижения требуемой точности ε

7. Объясните алгоритм решения нелинейного уравнения методом
простых итераций

8. Объясните схему алгоритма метода Ньютона

9. Объясните формулы итерационных процессов численного решения уравнений

ЛИТЕРАТУРА

1. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М.: Высшая школа, 1994.