Похибки при обчисленні наближених значеннях функції однієї змінної
Нехай задана деяка диференціальна функція у=f (х) і 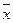 —наближене значення аргументу х.
—наближене значення аргументу х.
Наближеним значенням 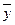 функції у вважають те значення, що вона приймає при наближеному значенні аргументу, тобто
функції у вважають те значення, що вона приймає при наближеному значенні аргументу, тобто 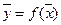 . Виникає питання про похибки цього наближення. Як відомо з курсу математичного аналізу, при досить малому приросту аргументу
. Виникає питання про похибки цього наближення. Як відомо з курсу математичного аналізу, при досить малому приросту аргументу 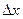 приріст функції
приріст функції  приблизно дорівнює її диференціалу:
приблизно дорівнює її диференціалу:
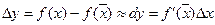 .
.
Звідси, якщо відомо абсолютну похибку аргументу 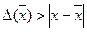 , абсолютну похибку функції можна визначити по формулі
, абсолютну похибку функції можна визначити по формулі
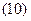
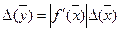 .
.
Відносна похибка функції, відповідно до формули (2),
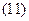
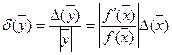 .
.
Як приклади визначимо абсолютні й відносні похибки деяких основних елементарних функцій.
1) Логарифмічна функція f(х)=logax. Абсолютна похибка логарифмічної функції, відповідно до формули (10), має вигляд
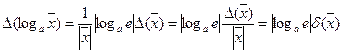 ,
,
де
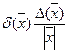 .
.
Зокрема, якщо a= 10, то lg e  0,5 й
0,5 й 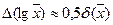 , якщо ж а=е, то
, якщо ж а=е, то 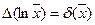 (lne=1). Абсолютна похибка логарифмічної функції з основою е дорівнює відносній похибці аргументу. Відносну похибку функції знаходимо по формулі (11):
(lne=1). Абсолютна похибка логарифмічної функції з основою е дорівнює відносній похибці аргументу. Відносну похибку функції знаходимо по формулі (11):
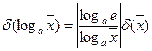 .
.
2) Степенева функція f(х) = 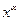 , де
, де 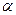 -будь-яке дійсне число.
-будь-яке дійсне число.
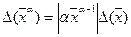 ,
,
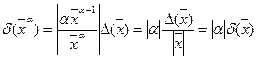 .
.
Слідуючи, відносна похибка степеневої функції пропорційна відносної похибці аргументу.
Зокрема,
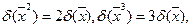
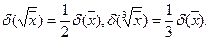
3) Показникова функція 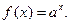
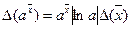 ,
,
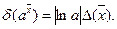
4) Тригонометричні функції f(x) = sіn x, f (х) = cos x.
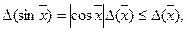
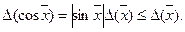
Отже, абсолютні похибці функцій синус і косинус не перевершують абсолютної похибки аргументу
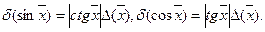
Похибки при обчисленні наближених значень функції декількох змінних
Розглянемо тепер диференційовану функцію, наприклад, трьох змінних 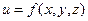 . Нехай
. Нехай 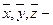 наближені значення аргументів х, у, z, обчислені з абсолютними похибками
наближені значення аргументів х, у, z, обчислені з абсолютними похибками 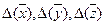 . Наближеним значенням
. Наближеним значенням 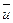 функції u вважають те значення, що вона приймає при наближених значеннях аргументів:
функції u вважають те значення, що вона приймає при наближених значеннях аргументів: 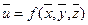 . Для визначення похибок, як й у випадку функції однієї змінної, скористуємося формулою диференціала, замінивши їм приріст функції:
. Для визначення похибок, як й у випадку функції однієї змінної, скористуємося формулою диференціала, замінивши їм приріст функції:
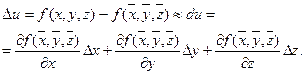
Абсолютну похибку 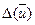 функції при відомих абсолютних похибках аргументів
функції при відомих абсолютних похибках аргументів 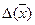 ,
, 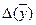 ,
, 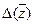 знаходимо по формулі
знаходимо по формулі
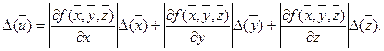
Відносну похибку, відповідно до формули (2), визначимо наступним виразом:

Зауваження. Похибки, що виникають при рішенні математичних задач чисельними методами, грубо можна розділити на дві групи. Першу групу становлять похибки, що не залежать від конкретного змісту задачі, а також похибки, викликані діями над наближеними числами. До другої групи відносяться похибки, що виникають за рахунок того, що математична задача як правило, заміняється спрощеною, близькою за результатом наближеної задачі. Ці похибки (похибки методу) визначаються залежно від характеру задачі.
Завдання 1
1) Визначити, яка рівність точніша.
2) Округлити сумнівні цифри числа, залишивши вірні знаки: а) у вузькому смислі; б) у широкому смислі. Визначити абсолютну похибку результату.
3) Знайти граничні абсолютні та відносні похибки чисел, якщо вони мають тільки правильні цифри: а) у вузькому смислі; б) у широкому смислі.
№1 1) 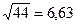 ;
; 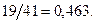 №2 1)
№2 1) 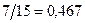 ;
; 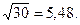
2) а) 22,553 ( 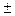 0,016); 2) а) 17,2834;
0,016); 2) а) 17,2834; 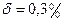 .
.
б) 2,8546; 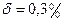 . б) 6,4257 (
. б) 6,4257 ( 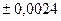 ).
).
3) а) 0,2387; б) 42,884. 3) а) 3,751; б).0,537.
№3 1) 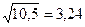 ;
; 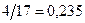 . №4 1)
. №4 1) 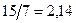 ;
; 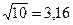 .
.
2) а) 34,834; 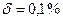 ; 2) а) 2,3485 (
; 2) а) 2,3485 ( 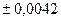 );
);
б) 0,5748 ( 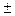 0,0034). б) 0,34484
0,0034). б) 0,34484 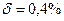 .
.
3) а) 11,445; б) 2,043. 3) а) 2,3445 б) 0,745.
Зразок виконання завдання
1) 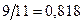 ;
; 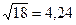 ; 2) а)72,353(
; 2) а)72,353( 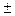 0,026); б) 2,3544;
0,026); б) 2,3544; 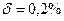 ;3) а)0,4357;
;3) а)0,4357;
б) 12,384.
1) Знаходимо значення даних виразів з великим числом десяткових знаків: а1= 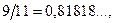 а2=
а2= 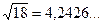 . Потім вираховуємо граничні абсолютні похибки, округляючи їх із залишком:
. Потім вираховуємо граничні абсолютні похибки, округляючи їх із залишком:
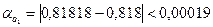 ,
, 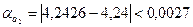 .
.
Граничні відносні похибки складають
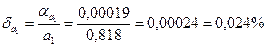
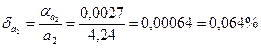
Так як 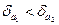 , то рівність
, то рівність 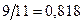 є більш точною.
є більш точною.
2) Нехай 72,353 ( 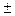 0,026)=а. Згідно умови, похибка
0,026)=а. Згідно умови, похибка 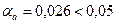 ; це значить, що в числі 72,353 вірні у вузькому смислі являються цифри 7, 2, 3. За правилами округлення знайдемо наближене значення числа, зберігши десяткові долі:
; це значить, що в числі 72,353 вірні у вузькому смислі являються цифри 7, 2, 3. За правилами округлення знайдемо наближене значення числа, зберігши десяткові долі:
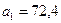 ;
; 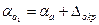 =0,026+0,047=0,073
=0,026+0,047=0,073
Отримана похибка більше 0,05, тобто треба зменшити число цифр у наближеного числа до двох:
а2=72; 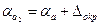 =0,026+0,353=0,379.
=0,026+0,353=0,379.
Так як 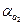 <0,5, то останні дві цифри вірні у вузькому смислі.
<0,5, то останні дві цифри вірні у вузькому смислі.
б) Нехай а=2,3544; 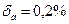 ; тоді
; тоді 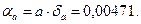 В даному числі вірними у широкому смислі являються три цифри, тому округлюємо його, залишаючи ці три цифри:
В даному числі вірними у широкому смислі являються три цифри, тому округлюємо його, залишаючи ці три цифри:
а1=2,35; 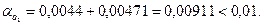
Значить, що і в округленому числі 2,35 всі три цифри вірні в широкому смислі.
3) а) Так як всі чотири числа а=0,4357 вірні у вузькому смислі, то абсолютна похибка 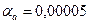 , а відносна похибка
, а відносна похибка 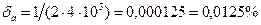 .
.
б) Так як всі п’ять цифр числа а=12,384 вірні у широкому розумінні, то  ;
; 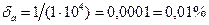
Завдання 2
Розрахувати і визначити похибку результату
№ 1
а) 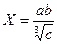 , a=3,85(±0,01), b=2,0435(±0,0004), c=962,6(±0,1)
, a=3,85(±0,01), b=2,0435(±0,0004), c=962,6(±0,1)
б)  ,
,
a=4,3(±0,05), b=17,21(±0,02), c=8,2(±0,05), m=12,417(±0,003), n=8,37(±0,005)
№ 2
а) 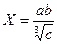 , a=4,16(±0,005), b=12,163(±0,002), c=55,18(±0,01)
, a=4,16(±0,005), b=12,163(±0,002), c=55,18(±0,01)
б) 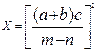 ,
,
a=5,2(±0,04), b=15,32(±0,01), c=7,5(±0,05), m=21,823(±0,002), n=7,56(±0,003)
№ 3
а) 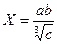 , a=7,27(±0,01), b=5,205(±0,002), c=87,32(±0,03)
, a=7,27(±0,01), b=5,205(±0,002), c=87,32(±0,03)
б) 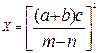 ,
,
a=2,13(±0,01), b=22,16(±0,03), c=6,3(±0,04), m=16,825(±0,004), n=8,13(±0,002)
№ 4
а) 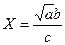 , a=228,6(±0,06), b=86,4(±0,02), c=68,7(±0,05)
, a=228,6(±0,06), b=86,4(±0,02), c=68,7(±0,05)
б) 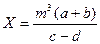 ,
,
a=13,5(±0,02), b=3,7(±0,02), m=4,22(±0,004), c=34,5(±0,02), d=23,725(±0,005)
Зразок виконання завдання
а) 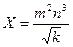 , m=28,3(±0,02), n=7,45(±0,01), k=0,678(±0,003)
, m=28,3(±0,02), n=7,45(±0,01), k=0,678(±0,003)
Знаходимо m2 = 800,9; n3 = 413,5; 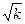 = 0,8234;
= 0,8234;
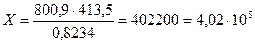
Далі, маємо 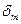 = 0,02/28,3 = 0,00071;
= 0,02/28,3 = 0,00071; 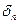 = 0,01 /7,45 = 0,00135;
= 0,01 /7,45 = 0,00135;
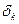 = 0,003/0,678 = 0,00443, звідки
= 0,003/0,678 = 0,00443, звідки
 = 2
= 2 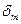 + 3
+ 3 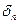 + 0,5
+ 0,5 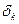 = 0,00142 + 0,00405 + 0,00222 = 0,00769 = 0,77%;
= 0,00142 + 0,00405 + 0,00222 = 0,00769 = 0,77%; 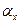 =4,02·105 ·0,0077 = 3,1·103.
=4,02·105 ·0,0077 = 3,1·103.
Відповідь. 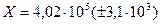 ;
;  = 0,77%.
= 0,77%.
б) 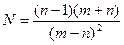 , n=3,0567(±0,0004), m=5,72(±0,02)
, n=3,0567(±0,0004), m=5,72(±0,02)
Маємо n-1 = 2,0567 ( ±0,0001); т + п=3,057 ( ±0,0004) +5,72 (± 0,02)= =8,777(±0,0204); т - п = 5,72 (±0,02)-3,057(±0,0004) = 2,663 (±0,0204);
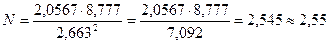 ;
;
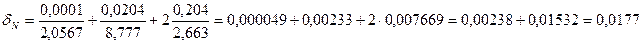 =1,77%;
=1,77%; 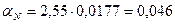 .
.
Відповідь.  ;
; 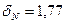 %.
%.
