Проекции цилиндра. Изображение цилиндра на чертеже. Точка и линия на поверхности цилиндра.

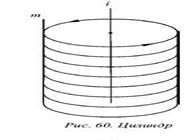
Цилиндр – это фигура, поверхность которого получается вращением прямой m вокруг оси i, расположенной в одной плоскости с этой прямой. В случае, когда прямая m направлена параллельно оси вращения, получается цилиндр (рис. 60), когда она пересекает ось вращения, полученная фигура будет являться конусом (рис. 61

Прямой круговой цилиндр имеет образующие, направленные перпендикулярно горизонтальной плоскости (рис. 61). По этой причине вне зависимости от выбора точки N на его поверхности горизонтальная проекция n этой точки находится на основании цилиндра.

Основание цилиндра составляет линию пересечения боковой поверхности цилиндра с горизонтальной плоскостью, т. е. это горизонтальный след поверхности цилиндра. Следовательно, боковая поверхность прямого кругового цилиндра, который стоит на горизонтальной плоскости, рассматривается как горизонтально-проецирующая поверхность по отношению к любой линии, начерченной на его поверхности.

На рисунке 63 показаны проекции цилиндра.

Фронтальная проекция а́а́₁, которая образует АА₁, ограничивает слева фронтальную проекцию цилиндра, т. е. является ее контурной образующей. На профильной плоскости ее проекцияа˝а˝₁располагается на оси симметрии этой проекции. Профильная проекция d˝d˝₁образующей DD₁является контурной, а ее фронтальная проекция d́d́₁ находится на оси симметрии и т. д.

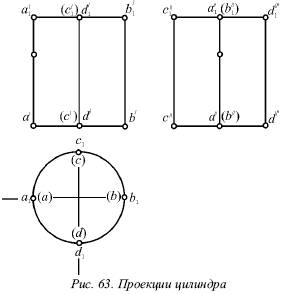
Если мы посмотрим на цилиндр сверху (рис. 63), увидим только его верхнее основание.

Рассмотрим горизонтальную проекцию. Если провести фронтальную плоскость Р, разделяющую цилиндр на две равные части, можно заметить, что все точки, лежащие на передней половине цилиндра, будут видны при рассмотрении цилиндра спереди, т. е. на фронтальной проекции. Боковая поверхность цилиндра, которая расположена ниже следа P_h, видима на фронтальной проекции, а остальная его часть невидима, т. е. образующая CC₁ на фронтальной проекции невидима.

Для выделения невидимых элементов на профильной проекции, необходимо обратиться к горизонтальной проекции. След Q_h профильной плоскости разделяет горизонтальную проекцию на две части. Боковая поверхность, которая расположена слева от Q_h, видима на профильной проекции и т. д. Таким образом образующая BB₁ невидима на профильной проекции.

Вид_на_чертеже

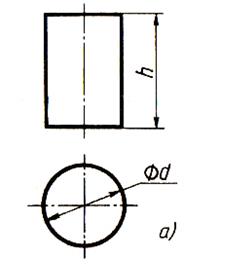
Положение точки на по­верхности вращения определяют по принадлежности точки ли­нии каркаса поверхности, т. е. с помощью окружности, проходящей через эту точку на поверхности вращения. В слу­чае линейчатых поверхностей для этой цели возможно приме­нение и прямолинейных образующих.

Применение параллели и прямолинейной образующей для построения проекций точек, принадлежащих данной поверхности вращения, показано на рисунке 7.12. Если дана проекция m' то проводят фронтальную проекцию f'f'₁ параллели, а затем радиусом R проводят окружность – го­ризонтальную проекцию параллели – и на ней находят проекцию m. Если бы была задана горизонтальная проек­ция m, то следовало бы провести радиусом

R = om окруж­ность, по точке f построить f' и провести f''f'₁ – фронтальную проекцию параллели – и на ней в проекционной связи отметить точку m'. Если дана проекция n' на линейчатом (коническом) участке поверхности вращения, то проводят фронтальную проекцию d's' очерковой образу­ющей и через проекцию n' – фронтальную проекцию s'k' образующей на поверхности конуса. Затем на горизонталь­ной проекции sk этой образующей строят проекцию п. Если бы была задана горизонтальная проекция n, то сле­довало бы провести через нее горизонтальную проекцию sk образующей, по проекции k' и s' (построение ее было рассмотрено выше) построить фронтальную проекцию s'k' и на ней в проекционной связи отметить проекцию n'.

На рисунке 7.15 показано построение проекций точки К, принадлежащей поверхности

тора. Следует отметить, что по­строение выполнено для видимых горизонтальной проекции к и фронтальной проекции k'.

На рисунке 7.16 показано построение по заданной фрон­тальной проекции m' точки на поверхности сферы ее гори­зонтальной m и профильной m''проекций. Проекция m построена с помощью окружности – параллели, проходящей через проекцию m'. Ее радиус – o–1. Проекция m" построена с помощью окружности, плоскость которой параллельна профильной плоскости проекций, проходящей через проек­цию m'.Ее радиус o"2".

Построение проекций линий на поверхности вращения мо­жет быть выполнено также при помощи окружностей – па­раллелей, проходящих через точки, принадлежащие этой линии.

На рисунке 7.17 показано построение горизонтальной про­екции ab линии, заданной фронтальной проекцией a'b' на по­верхности вращения, состоящей из частей поверхностей сферы, тора, конической. Для более точного вычерчивания горизон­тальной проекции линии продолжим ее фронтальную проек­цию вверх и вниз и отметим проекции 6' и 5' крайних точек. Горизонтальные проекции 6, 1, 3, 4, 5 построены с помощью линий связи. Проекции b, 2, 7, 8, а построены с помощью параллелей, фронтальные проекции которых проходят через проекции b', 2' 7', 8' a' этих точек. Количество и располо­жение промежуточных точек выбирают исходя из формы ли­нии и требуемой точности построения. Горизонтальная проекция линии состоит из участков: b –1 – части эллипса, 3 – 8 – a – 4 – части эллипса,

1 – 2 – 7 – 3 – кривой четвертого порядка (проекция кривой на поверхности тора).

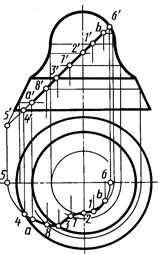
Рис. 7.17