Основные теоремы о пределах

Лекция 4. Основные теоремы о пределах функции. Асимптотические приближения. Непрерывность функции. Основные теоремы о непрерывных функциях. Точки разрыва. Классификация точек разрыва.

Основные теоремы о пределах

Предполагается, что функции, рассматриваемые в следующих теоремах определены на некотором общем множестве Х, для которого точка а является предельной точкой.

Теорема 1

Если каждое слагаемое алгебраической суммы конечного числа функций имеет предел при 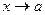, то предел этой алгебраической суммы при 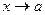существует и равен такой же алгебраической сумме пределов слагаемых.

Доказательство

Рассмотрим алгебраическую сумму трех функций f(x)+g(x)-h(x), где

, , .

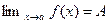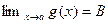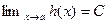Так как функции отличаются от своих пределов на бесконечно малые, то получаем

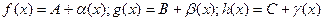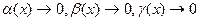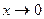(1), где при . Из равенств (1), используя теорему об алгебраической сумме бесконечно малых будем иметь

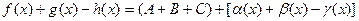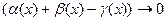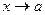(2), где при . Из равенства (2) вытекает, что сумма f(x)+g(x)-h(x) отличается от A+B+C на бесконечно малую функцию и следовательно, это число является пределом данной суммы. Таким образом, имеем

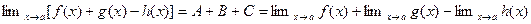(3). Теорема доказана.

Следствие

Функция может иметь только один предел при .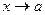

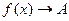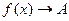Действительно, если и ’ при 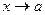, то на основании теоремы 1 получим 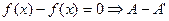при 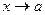. Так как предел постоянной функции равен самой функции и единственен, то имеем A-A’=0, то есть A=A’.

Замечание

В условии теоремы предполагалось, что каждая из функций имеет предел и доказывалось, что их сумма также имеет предел. Обратное в общем случае неверно, то есть из существования предела суммы не следует существование пределов слагаемых.

Пример

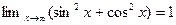, тогда как 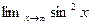не существует и 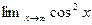не существует.

Теорема 2

Если каждый из сомножителей конечного числа функций имеет предел при 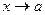, то предел произведения при 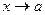существует и равен произведению пределов сомножителей.

Доказательство

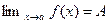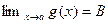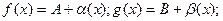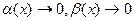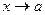1) Рассмотрим сначала произведение двух сомножителей f(x)g(x) и пусть , . Имеем (4), где при . Отсюда получаем 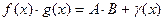(5),

где 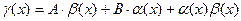(6). Из основных теорем о бесконечно малых (теорема 1,2,3) следует, что 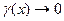при 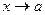. Поэтому на основании равенства (5) будем иметь 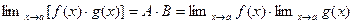(7)

2) Рассмотрим случай произведения трех функций f(x)g(x)h(x), имеющих конечные пределы при 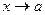. Используя первую часть доказательства находим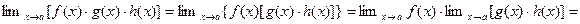

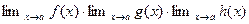
Следствие 1

Постоянный множитель можно выносить за знак предела.

Пусть С – постоянная функция,

тогда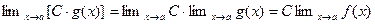

Следствие 2

Если функция f(x) имеет предел при 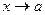, то предел при 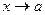целой положительной степени ее равен такой же степени предела этой функции, то есть

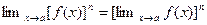
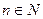
Пример

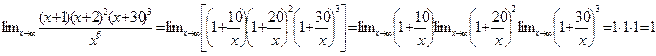
Лемма

Пусть 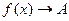при 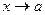. Тогда обратная по величине функция 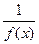ограничена в некоторой окрестности 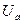точки а.

Доказательство

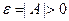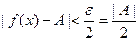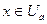Положим . На основании определения предела функции имеем при . Отсюда получаем

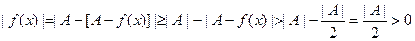при 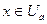. Таким образом,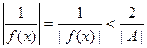

Теорема 3

Если функция f(x) имеет предел при 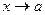, отличный от нуля, то предел обратной ей по величине функции 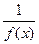равен обратной величине предела данной функции, то есть 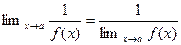(8)

Доказательство

Пусть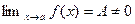

Тогда на основании леммы и учитывая, что произведение ограниченной функции на бесконечно малую функции, есть бесконечно малая функция, будем иметь

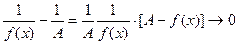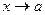при . Отсюда получаем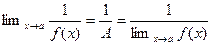

Теорема 4

Если делимое f(x) и делитель g(x) имеют пределы при 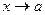и предел делителя отличен от нуля, то предел их частного при 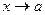равен частному пределов делимого и делителя, то есть

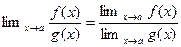(9)

Доказательство

Пусть 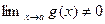. Тогда, используя теорему о пределе произведения (теорема 2) и теорему о пределе обратной величины функции (теорема 3), получим

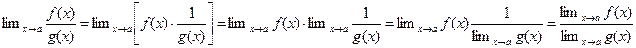Пример

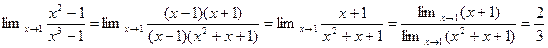
Теорема 5

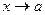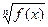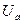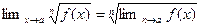Если функция f(x) имеет предел при и (n – натуральное) существует в точке а и в некоторой ее окрестности , то (10)